Bigelow and Pargetter, Doctrine of Change
본 글은 2020-1학기 포항공대 이충형 교수님의 ‘시공간과 물질의 철학’ 수업의 읽기자료의 내용을 정리한 것입니다. 물리학도는 아니지만 수업의 본질에 다가가고자 이렇게 문서형태로 정리해둡니다. 지적은 언제나 환영입니다 :)
읽기자료:
Science and Necessity, Bigelow & Pargetter, 1991
우리는 벡터를 다루면 꼭 짚고 넘어가야 하는 ‘변화란 무엇인가problem of change‘를 살펴볼 것이다. 그리고 아주 특별한 케이스인 ‘운동이란 무엇인가problem of motion‘에 대해서도 살펴볼 것이다.
자! 우리는 지금부터 변한다는 성질에 내재하는 모순점에 대해 논의해보자.
Ockhamist vs. Doctrin of Flux
우리는 변화에 대한 두 가지 관점을 살펴볼 것이다.
변화란 “서로 다른 시간에 서로 다른 성질들의 배열이 점유하는 것 change is nothing more than the possession of a sequence of different properrties at different times“이라고 주장하는 Doctrine of Changing Form과 이것과 반대되는 Doctrine of Change of Form에 대해서 살펴볼 것인다. (솔직히 이름이 너무 비슷하다 ㅜㅠ)
그래서 좀더 알아듣기 쉽게,
Doctrine of Changing Form = Ockhamist 또는 오컴파
(Ockham과 그의 추종자들이 주창해서)
Doctrine of Changing Form = Doctrine of Flux = Flux파
(왜 이렇게 부르는지는 다음 설명을 들어보자!)
라고 부를 것이다.
Doctrine of Flux는 변화 자체를 “어떤 시간에 물체가 가지는 성질 change it self is a characteristic of a thing at a time“이라고 정의한다. 예를 들어 불빛이 어두워짐에 따라 물체가 회색에서 검은색으로 바뀌는 현상을 Doctrine of Flux는 물체가 어두워지는 현상 자체를 물체의 속성이라고 정의한다.
두 주장은 운동motion: change of place에 대해서도 서로 다른 의견을 제시한다!!
오컴파는 운동을 “motion is the occupation of successive places at successive times” 이라고 주장하며,
Flux파는 “moving body possesses not only a position, but also what amounts to an instantaneous velocity” 이라고 주장한다. 1
오컴파와 Flux파가 vector를 다루는 방식이 약간 다른데, Flux파가 우리가 평소 다루는 방식대로 방향과 함께 (순간) 속도를 다룬다면 오컴파는 물체의 위치 변화의 배열sequence of position로 vector의 방향을 기술하고, 뒤이어 mathematical limit를 사용해 순간 속도라 불리는 것을 정의한다. 오컴파도 어찌어찌 순간 속도를 정의는 했지만 이것을 물체의 내재적 속성intrinsic property으로 여기지는 않는다.
속성의 위계
논의를 이어가기 전에 OO’속성’으로 불린다고 다 똑같은 것은 아니라는 점을 짚고 넘어가야 한다. 어떤 속성은 더 우위에 있기도 하고, 어떤 속성은 더 본질적이다..
-
First-Order & Second-Order Property 1차 속성 & 2차 속성2
First-order property는 물체가 해당 속성을 가지는지 바로 결정 또는 묘사할 수 있는 속성이다. 무게나 전하량 등이 여기에 속한다.
Second-order property는 다른 물리적 속성의 도움을 받아야만 정의될 수 있는 성질이다. 우리의 심리적 상태나, 생각이 여기에 속한다.
여기서 유의할 점은Second-order property로 아무리 날고 기어도 절대First-order property를 정의하거나 설명할 수 없다는 것이다. 이것을 기준으로(순간)속도에 대한 논의가 진행된다. -
Primary & Secondary Property 제1성질 & 제2성질
Primary property는 물체가 어떤 상황에 있더라도 결코 분리될 수 없는 성질이다. 수(數), 형태, 크기가 여기에 속한다.
Secondary property는 우리의 감각과 관념에 의해 인지되는 주관적인 성질이다. 색, 향기, 소리, 맛 등이 여기에 속한다.
사실 2번 분류는 굳이 필요없는 것이긴 하다. 하지만 자료를 찾다보니 1번과 정의가 너무 비슷해서 헷갈릴까봐 함께 정리해둔다.
문헌과 자료에 따라 속성이 무엇을 의미하는지, 정의나 이미지가 조금씩 다른 것 같다. (특히 intrinsic property) 그래서 글의 문맥을 보고 해당 속성에 대한 것을 파악하는 자세가 필요해보인다.
오컴파 vs. Flux파: 속도
Flux파는 vector를 통해 위치 변화를 기술할 수 있다고 주장한다. 또한, 위치 변화로 vector가 정의되는 일은 절대 불가능하다고 말한다.
The velocity vector explains change of position, not because it is defined by change of position.
그리고 덧붙여 The presence of a vector at a time will contribute to an explanation of its subsequent positions. 라고 말한다.
하지만 오컴파는 velocity가 물체의 위치 변화에 의해서 기술되는 것이라고 주장한다. a certain velocity just because it has been in different places
그!리!고!
오컴파는 position은 1차 속성이며, velocity는 2차 속성이라고 정의하였다!!
덧붙여 what constitutes velocity is a second-order pattern over first-order positions at times.라고 주장한다.
반!면!
Flux파는 position과 (instantaneous) velocity 모두 1차 속성이라고 정의한다.
이때, 1차 속성끼리는 서로를 설명할 수 있으므로, position에 대한 정보가 있을 때 velocity를 설명할 수 있고, velocity에 대한 정보가 있다면, 물체의 position을 설명할 수 있다고 말한다.
자! 이제 두 주장이 하나의 물리 현상을 어떻게 설명하는지 살펴보자.
Three Newtonian Rigid Sphere A, B, and C
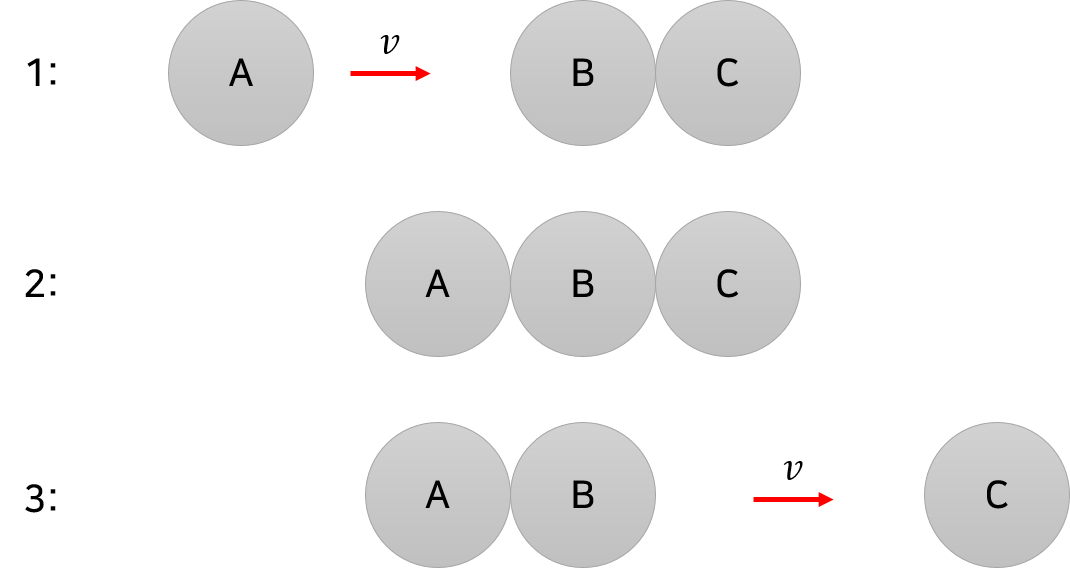
위와 같은 탄성 충돌 상황에 대해 오컴파와 Flux파의 설명이 다르다!!
1번과 3번 과정에 대해서는 오컴파와 Flux파의 주장은 동일하다. 하지만, 2번 과정에 대해서는 둘의 설명이 달라진다!!
먼저 우리가 익숙한 Flux파의 관점에서 설명하자면,
A와 B가 충돌할 때, A의 순간속도가 B에 전해진다. 그리고 B가 잠시나마 v의 순간속도를 가지며, 이것이 C에게 v의 순간속도로 전달된다.
라고 설명한다. 이때 눈여겨 볼 점은 B는 과거-미래에 아무런 움직임도 없는데, v라는 속도를 잠깐이나마 가지게 된 점도 흥미롭다.
반면, 오컴파는
2번 상황에서 B는 움직임이 없으므로 0의 속도를 가진다. 그러다가, 갑자기 C가 v의 속도를 가지며 앞으로 나아간다.
라고 설명한다.
뭔가 오컴파의 설명에 의심의 눈초리를 보내게 된다 ㅡ.ㅡ
실제로 약간의 문제가 있는데, 오컴파의 설명이 맞다면 이것은 원격 작용action at a distance을 긍정하는 것이 되어버린다!
본인도 원격작용이 뭔지 정확하게는 잘 모르지만, 이것이 우리가 느끼는 현실세계와 호응하지 않는다는 것은 분명하다.3
Movement of an Image projected onto a screen from a movie projector
오컴파는 그들의 주장을 정당화하기 위해 다음과 같은 상황을 제시한다.
프로젝터가 스크린 위에 영화를 상영하고 있다고 생각해보자. 그러면 영화에 등장하는 순간순간의 장면들에 존재하는 물체는 순간속도를 지니지 않는다. 그들은 한 장소와 시간에 생성되었다가 소멸된 후, 다른 장소와 시간에 다시 생성될 뿐이다.
그래서 이 상황에 따르면, 물체의 움직임에 순간속도를 도입할 필요가 없다고 주장한다.
그리고 스크린 속 물체는 매순간마다 생성되는 것이므로, 스크린 속 물체가 다음 장면에서 어떻게 이동할 지 역시 예측할 수 없다고 주장한다. 스크린 속 물체의 미래-과거를 결정하는 것은 오직 프로젝터 그 자체이다!4
심지어 우리가 동일한 장소라고 인식하는 것 역시 사실은 동일한 장소가 아니라고 주장한다!!
이것은 “지금의 우리와 1초 후의 우리가 전혀 다른 존재”라는 말인데,
‘지금’의 우리는 ‘지금’이 지나면 소멸되고, 바로 다음 ‘순간’에 다시 생성되고, 다시 소멸하고, … (반복) … 그래서 1초 후의 우리는 지금의 우리와는 다른 존재이다!5
라고 주장한다.
정말 말도 안 되는 주장이지만, 이것을 부정할 근거는 없다 ㅜㅠ
Flux파: 등속도 운동Continuing motion은 변화가 아니다.
Doctrine of Flux를 바탕으로 할 때, 주장할 수 있는 엉뚱한 주장인데
만약 순간속도를 물체의 고유한 특성으로 여기고, 물체의 위치 변화를 외적인 변화로 설정해보자. 그러면 등속도 운동 상황에서는 물체의 고유한 특성이 바뀌지 않으므로, 등속도 운동을 변화change라고 볼 수 없다!
오컴파 vs. Flux파: 운석 충돌에 대한 설명
어떤 현상에 대해 오컴파와 Flux파의 시각에서 설명의 차이가 생기는 적절한 경우로 저자는 ‘화성에 운석이 충돌’하는 상황을 제시한다.
오컴파는 운석 충돌을 예측하기 위해 운석이 지금까지 겪은 과거의 위치에 대한 정보가 필요하다.
반면, Flux파는 운석 충돌을 예측하기 위해 과거의 정보를 가져올 필요 없이, 현재와 앞으로 운석이 가질 순간속도에 대한 정보만으로 충분하다.
운석의 과거 궤적에 대한 정보가 필요하다는 오컴파의 주장은 아쉽게도 우리가 운석의 과거 궤적에 대한 정보를 알 수 없기에 운석 충돌을 예측하는데 부족함이 있다 ㅜㅠ
결론
저자는 최종적으로 Flux파의 주장에 동의한다.
본인도 자연 현상을 좀더 잘 설명하는 Flux파가 적절한 이론이라고 생각한다.
하지만, 영화-프로젝터의 상황처럼 때에 따라서는 오컴파의 관점도 필요하다고 생각한다.
결론적으로 두 주장을 조화롭게, 필요한 곳에 적절히 사용하는 것이 중요하지 않나 싶다.
-
Flux파에서instantaneous velocity개념이 등장했는데, 뉴턴이 미적분학(Calculus)를 Theory of Fluxions라고 이름 붙인 것을 바탕으로 저자는 反오컴파를Doctrine of Flux라고 이름 붙였다. ↩ -
정말 이렇게 부르는지는 잘 모르겠다. 아무리 찾아봐도 번역된 말이 없어서, 그냥 교수님이 수업 때 부른대로 기술해뒀다. ↩
-
미시세계에서도
원격작용이 가능할 수도 있을 것 같기에, 미시세계에서의 명제는 보류하도록 하자! ↩ -
오컴파는 이것을 바탕으로 우리의 세상 역시 하나의 ‘영화’일 뿐이며, 우리의 과거-미래는 ‘신’이라는 프로젝터에 의해 결정되는 것이라고 덧붙인다. ↩
-
컴공과적인 생각을 도입하자면, 매순간순간마다 ‘나’라는 인스턴스가 생성-소멸을 반복되는 것이다! ↩
