Maudlin, Classical Accounts Of Space And Time
본 글은 2020-1학기 포항공대 이충형 교수님의 ‘시공간과 물질의 철학’ 수업의 읽기자료의 내용을 정리한 것입니다. 물리학도는 아니지만 수업의 본질에 다가가고자 이렇게 문서형태로 정리해둡니다. 지적은 언제나 환영입니다 :)
읽기자료:
Ch.01: Classical Accounts of Space and Time, from Philosophy of Physics: Space and Time, Tim Maudlin, 2012
처음 부분에는 고대의 철학이 물리학을 어떻게 정의했는지에 대한 내용이 나온다. 굳이 정리하지 않아도 중학교 때부터 배운 내용이라 생략 or 간략화하겠다.
아리스토텔레스Aristotle의 물리학
Aristotle defined the nature of an object as an internal source of motion and rest that belongs to an object primarily and properly and nonaccidentally.
Thus, for Aristotle, the nature of an object is revealed by how the object moves, and stops moving.
돌맹이가 땅으로 떨어지는 것, 물 속의 기포가 올라가는 것 모두 물체가 가지는 고유한 ‘본성’에 의해 그렇게 움직이는 것이다.
그래서 등장한 것이 4원소설!!
흙 & 물은 아래로 떨어지려는 본성을 가진다.
불 & 공기는 위로 상승하려는 본성을 가진다.
여기에 태양과 달처럼 하늘에서 원운동하는 물체를 설명하기 위해 제5원소인 에테르aether를 도입한다.
아리스토텔레스는 아래로 떨어지려는 본성이 “특정 장소로 가려는 성질”로 설명하는데, 그 특정 장소란 우주의 중심이라고 주장한다.
아리스토텔레스는 우주가 유한한 구형 모양으로 여기고, 구의 껍질에는 별들이 박혀있다고 주장했다. 그리고, 지구의 중심이 우주의 중심이기에 흙 & 물이 아래로 향하는 것이 사실은 중심을 향해 움직이는 현상이라고 설명했다.
아리스토텔레스의 물리학에서는 운동과 함께, 우주관을 곁들여 설명한다. 아리스토텔레스의 우주관이 유럽의 고대-중세 물리학의 발전에도 기여했지만, 동시에 얽어매기도 했다. 아리스토텔레스의 물리학은 이후 케플러Kepler 법칙이 등장한 1600년대에 이르러서 조금씩 깨지기 시작한다.
뉴턴 제1법칙과 뉴턴의 절대시공간
Law I
| Every body preseverse in its state either of rest or of uniform motion in a straight line, except insofar as it is compelled to change its state by impressed forces. |
뉴턴 제1법칙 하나만으로 아리스토텔레스의 물리학은 크게 흔들린다.
-
뉴턴 제1법칙은 모든 물체에 대해 적용된다.
Newton’s law governs every body. -
뉴턴 제1법칙 물체 하나하나에 대해 특정한 운동의 본성을 정의하지 않는다.
Newton does not ascribe any particular natural motion to a body.제1법칙은 모든 물체가
관성Inertia이라는 성질을 가지고 있어 가진의 운동 상태를 유지하려는 경향이 있다고 설명한다. 그리고 우주에는 본성에 의해 가게 되는 특정 장소가 존재하지 않는다고 설명한다. 즉,우주의 중심은 없다고 말한다.
그리고 뉴턴은 운동이 절대시공간Absolute space라는 경기장 안에서 이루어진다고 주장한다. 그리고 운동은 이 공간에서 물체의 위치가 변하는 것일 뿐이라고 말한다.
뉴턴은 자신의 물리학을 절대시공간 안에서 기술했기 때문에, 이게 못 미덥더라도 일단은 이것을 인정하고 이 녀석의 성질들을 바탕으로 운동을 파악해야 한다 ㅜㅠ
뉴턴의 절대시공간
절대시공간은 3차원의 유클리드 공간이다.
간단하게 이것을 $E^3$라고 표기하자. 그러면 아리스토텔레스의 우주와 다르게 $E^3$는 모든 방향에서 무한하게 정의되기 때문에 기하학적 중심이 존재하지 않는다!
그리고 당연하게도 $E^3$ 공간 내에 존재하는 물체들은 유클리드 기하학의 공리axiom들을 만족한다.
-
Topology
기하학적 구조geometric structure가 가져야 할 가장 기본적인 성질은Topology이다.
우리는 Topology를 통해continuity를 보장할 수 있는데,
펜을 한번도 떼지 않고, 유클리드 도형을 그려낼 수 있다는 말이다. 그리고 이것을 통해 공간 상에 존재하는 선line과 그것과 끊어진 선을 구분할 수 있게 된다.Topology를 rubber-sheet geometry라고 부를 수도 있는데,
찢어지거나 덮이지 않는 고무판 위에 그린 도형을 생각해봤을 때, 우리가 아무리 구부리거나 펴도 도형이 가지는 변하지 않는 성질이 있다는 말이다.
예를 들어 변형deformation을 가하기 전에 intersect하는 선은 변형을 하고 난 후에도 여전히 intersect하고 있다.만약 Topology가 보장되지 않는다면, 우리는 connected와 disconnected를 구분하지 못할 것이다.
-
Affinity = straight-edge
유클리드 기하학의 첫 두 가정은 다음과 같다.a. It is possible to draw a straight line from any point to any point.
b. It is possible to extend any finite straight line continuously in a straight line.이것은 1번의 Topology만으로는 충분히 보장되지 않는다. 그래서 a, b번의 조건을 만족하는 기하학적 구조를 우리는
Affine Structure라고 부른다.Affine 구조는 유클리드 공간 상의 어떤 두 점의 쌍pair을 잡아도 그 둘을 끝점으로 가지는 직선을 그을 수 있다고 한다. 그리고 어떤 유한 직선을 잡더라도 그것을 무한 직선으로 연장할 수도 있다!
만약 Affinity가 보장되지 않는다면, 우리는 어느 시점에는 선분을 연장하는 것이 가로막힐 것이다.
-
Metric = distance & length
1번의 Topology와 2번의 Affinity 모두 길이length나 거리distance에 대한 것을 보장하지 않는다. 그래서 우리가 저 두 성질을 보장받으려면, 또다른 기하학적 구조인Metric에 대해서 정의해야 한다.유클리드 기하학은 세 번째로 다음을 가정한다.
c. A complete, continuous, closed circle can be drawn with any given center and radius.
그리고 우리는 컴퍼스compass를 통해서 이것을 보장할 수 있다.
지금까지 우리는 유클리드 공간에서 정의되는 세 가지 수준의 구조를 살펴보았다. 이제 이것을 세 가지 다른 형태의 변환transformation으로 정의하여 각가이 유클리드 공간에서 어떻게 기능하는지 살펴볼 것이다.
-
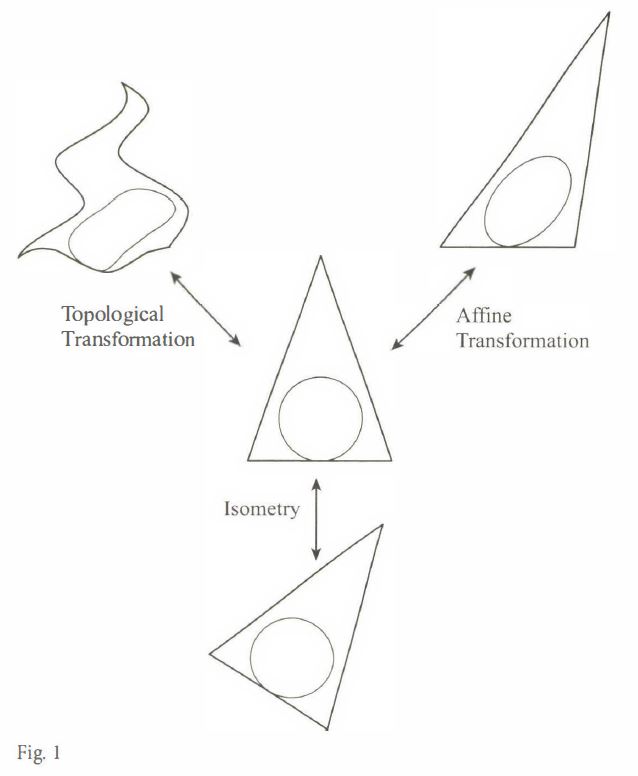
Topological Transformation
연결된 직선이 끊어지지 않는다.
carries continuous lines into continuous lines. -
Affine Transformation
직선을 직선으로 매핑한다.
map straight lines onto straight lines.
두 점 사이의 거리가 멀어지거나, 원circle이 타원ellipses으로 변할 수 있다. -
Isometry
거리distance를 보존하며 매핑한다.
map from a space onto itself that preserves distance.
그래서 원이 그대로 원으로 보존된다.
이때, 흥미로운 사실은 각 Transformation에 위계가 있다는 것이다!
모든 Isometry는 Affine Transformation의 특수한 경우이고,
Every isometry is an affine transformation.
모든 Affine Transformation은 Topological Transformation의 특수한 경우이다.
Every affine transformation is a topological transformation.
저자는 3가지 기하학적 구조에 덧붙여 Topological structure와 Affine structure 사이에 존재하는 Differentiable structure를 제시한다!!
이것은 매끈한smooth 곡선과 뾰족한sharp 곡선을 구분하는 기하학적 구조이다.
그리고 이 성질을 보존하는 변환을 Diffeomorphism이라고 하며, 매끈한 곡선을 매끈한 곡선으로 매핑한다. map smooth curves into smooth curves.
기존 변환들과의 차이점은 Topological transformation은 삼각형을 원으로 변환할 수 있지만, Diffeomorphism에서는 그럴 수 없다!
자!
이제 $E^3$가 정말로 뉴턴 제1법칙에 적합한 공간인지 등속직선운동을 바탕으로 검증해보자.
먼저, 물체가 연속적인 운동을 하려면 그 공간은 Topology를 가져야 한다. 만약 Topology가 결여되어 있다면, 우리는 운동의 연속성을 구분하지 못한다!
그리고 물체가 직선 운동하려면 Affine Structure가 필요하며, 물체가 등속으로 운동하는지 판단하려면 Metrical Structure가 필요하다! 왜냐하면 같은 시간 간격 동안 동일한 ‘거리’를 움직였는지 판단해야 하기 때문에, 거리를 측정하는 도구가 필요하다.
뉴턴의 절대시간
그는 운동이 $E^3$의 경기장에서 존재한다고 생각했고, 그리고 이 경기장이 매 순간마다 존재한다고 생각했다.
뉴턴 제1법칙의 상황 아래, 물체가 정지에 했다고 생각해보자. 그런데 우리는 이 물체가 정지해있음을 어떻게 알 수 있을까??
뉴턴은 물체가 정지해있음을 다음과 같이 정의한다.
A body is at absolute rest when it occupies the same points of absolute space over a period of time.
그리고 물체가 움직이는 것에 대해서는 absolute uniform motion in a straight line1을 제시한다. 이것에 따르면 움직이는 물체는 절대 공간absolute space안에서 어떤 궤적trajectory을 가진다. 그리고 이 궤적을 설명하기 위해 시간이 Topology와 Affinity를 가진다고 주장한다.
그리고 uniform은 같은 시간 간격 동안 같은 거리를 움직이는 것이라고 설명한다. it covers the same distance in the same time. 여기서 ‘같은 시간 간격’이라는 말을 보장하기 위해 시간이 Metric 성질을 가진다고 주장한다.
결론적으로 뉴턴 제1법칙은 절대공간과 함께 절대시간을 전제로 한다.
뉴턴이 주장하는 절대시간은 Topology, Affinity, Metric을 모두 만족하는 1차원 구조이다.
뉴턴은 절대시간에 방향성이 존재한다고 주장했다. 여기서 시간에 방향성이 존재하는지 여부와 뉴턴의 운동법칙이 성립하는지는 별개의 문제이다. 다만, 당시의 자연스러운 생각으로는 시간이 과거→미래로 흐르니, 시간에 방향성이 존재한다고 주장해도 그려려니 한다.
뉴턴은 제1법칙의 ‘정지’와 ‘운동’을 설명하기 위해 우리의 오감으로 느낄 수는 없지만 객관적으로 존재는 하며, 움직이지도 변하지도 않는 절대공간이 있다고 주장했다. 하지만 우리는 공간을 인식하거나 물체의 운동을 관찰할 때, 공간을 ‘상대적’으로 이해한다. 그리고 이 상대공간을 이용해 현상을 기술한다.
뉴턴이 생각하는 절대공간이 실제로 있는 것인지 우리는 검증할 방법이 없다. 다만, 우리는 절대공간을 어떤 상대적인 공간에 표상할 뿐이며 운동을 ‘상대적’인 방식으로 이해할 수 밖에 없다.
-
uniform motion에 직선 운동만 있는 것은 아니다. uniform circular motion도 가능하다. ↩
