Locally Weighted Linear Regression, MLE ≡ LMS

본 글은 2018-2학기 Stanford Univ.의 Andrew Ng 교수님의 Machine Learning(CS229) 수업의 내용을 정리한 것입니다. 지적은 언제나 환영입니다 :)

– lecture video

---

Locally Weighted Linear Regression; LWR

지난 강의에서는 Linear Regression에 대한 다뤘다면, 이번에는 Weight 함수 $w^{(i)}$가 포함된 Locally Weighted Linear Regression_LWR에 대해 다룬다.

LWR은 함수를 근사할 때, neighborhood의 영향을 더 고려하자는 패러다임이다. 그래서 LWR은 다음의 수정된 Cost function을 사용한다.

$$\sum_{ i } { w^{(i)} {\left( y^{(i)} - {\theta}^{T} x^{(i)} \right)}^{2} }$$

이때, Weight 함수 $w^{(i)}$은 다음과 같다.

$$w^{(i)} = \textrm{ exp } \left( - \cfrac{1}{2} {\left( x^{(i)} - x \right)}^{2} \right)$$

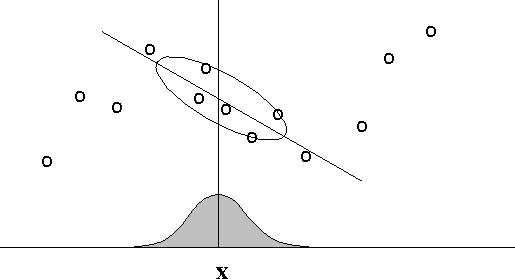
$w^{(i)}$의 의미를 해석해보면,

• if $\left| x^{(i) - x }\right|$ is small, $w^{(i)} \approx 1$
• else if $\left| x^{(i) - x }\right|$ is large, $w^{(i)} \approx 0$

그래서 $\theta$는 query point $x$와 가까운 점들에 대해 더 큰 weight를 부여한다.

$w^{(i)}$는 Gaussian과 비슷한 형태를 가지지만, $w^{(i)}$가 Gaussian function인 것은 아니다!

$w^{(i)}$는 neighborhood의 범위를 neighborhood parameter $\tau$를 통해 지정한다.

$$w^{(i)}(x; \tau) = \textrm{ exp } \left( - \cfrac{1}{2 \tau^{2}} {\left( x^{(i)} - x \right)}^{2} \right)$$

parametric / non-parametric Learning

$w^{(i)}$는 입력값 $x$에 대한 함수이다. 그래서 $w^{(i)}(x)$라고 할 수 있다.

“weights depend on the particular point $x$ at which we’re trying to evaluate $x$.”

LWR를 통해 Learning을 할 경우 weight $\theta$는 특정 입력값 $x$에 따라 바뀐다. 그래서 입력값이 바뀔 때마다 $\theta$를 매번 다시 최적화해야 한다.

LWR은 대표적인 non-parametric Learning이다. 앞에서 살펴본 (unweighted) Linear Regression은 parametric Learning에 해당한다. 그 이유는 Linear Regression에서는 dataset이 고정되어 있고 Learning을 통해 최적화한 $\theta$ 값을 알고 있으면, 그 이후의 prediction은 Learning 없이 해당 $\theta$ 값만을 사용하면 되기 때문이다.

“Once we’ve fit the $\theta_{i}$’s and stored them away, we no longer need to keep the training data around to make future predictions.”

하지만 non-parametric Learning에서는 dataset이 고정되어 있지 않고, 매 prediction마다 query point $x$에 따라 Learning을 새롭게 해줘야 한다. 계산 비용은 매우 크지만, Linear Regression보다 더 낮은 prediction error를 보인다.

---

Probabilistic Interpretation

우리는 지금까지 LMS_{Least Mean Square} 방식으로 Cost를 정의하여 $\theta$를 Learning 하였다. 왜 하필 LMS을 사용한 것일까? LMS 방식이 왜 합리적인지 그 이유를 Probability 관점에서 살펴보자!

Maximum Likelihood Estimation

먼저 target variable $y^{(i)}$와 input variable $x^{(i)}$가 다음과 같은 관계를 가진다고 가정하자.

$$y^{(i)} = \theta^{T} x^{(i)} + \epsilon^{(i)}$$

$\epsilon^{(i)}$은 error term으로 modeling 과정에서 포함하지 못한 feature나 random noise를 포함한다.

또, $\epsilon^{(i)}$에 대해서는 Gassian distribution을 따르는 IID_{Independently and Identically distributed}라고 가정한다. (“Normal distribution”이라고도 한다.)

$$\epsilon^{(i)} \sim N\left( 0, \sigma^{2} \right)$$

”$\epsilon^{(i)}$가 IID”라고 함은 house1의 error term이 house2의 error term에 영향을 주지 않는다는 말이다.

$\epsilon^{(i)}$에 대한 확률 분포를 수식으로 기술하면,

$$p( \epsilon^{(i)} ) = \frac{ 1 }{ \sqrt{2\pi} \sigma } \textrm{ exp } \left( - \cfrac{ {\left( \epsilon^{(i)} \right)}^{2} }{2 \sigma^{2}} \right)$$

이때, 식 $y^{(i)} = \theta^{T} x^{(i)} + \epsilon^{(i)}$에 의해서 $\epsilon^{(i)} = y^{(i)} - \theta^{T} x^{(i)}$이다. 따라서 $p\left( \epsilon^{(i)} \right)$는 다음을 의미한다.

$$p ( y^{(i)} \vert x^{(i)}; \theta ) = \frac{ 1 }{ \sqrt{2\pi} \sigma } \textrm{ exp } \left( - \cfrac{ {\left( y^{(i)} - \theta^{T} x^{(i)} \right)}^{2} }{2 \sigma^{2}} \right)$$

¹

확률 함수 $p ( y^{(i)} \vert x^{(i)}; \theta )$는 $\theta$를 인자로 하는 Likelihood 함수 $L(\theta)$로 해석할 수도 있다.

$$L(\theta) = L(\theta; X, \vec{y}) = p(\vec{y} \vert X; \theta)$$

$\theta$가 변수인지 고정값인지에 따라 $L(\theta)$와 $p(\vec{y} \vert X; \theta)$를 사용한다.

$\theta$가 변수라면, Likelihood $L(\theta)$를 사용한다. 반면, $\theta$가 고정되어 있고, $(y, x)$ 같은 training pair가 변한다면, $p(\vec{y} \vert X; \theta)$를 통해 “probability of data”의 의미로 사용한다.

$p(\vec{y} \vert X; \theta)$는 IID에 의해 다음과 같이 표현된다.

$$p(\vec{y} \vert X; \theta) = \prod _{ i } { p(y^{(i)} \vert X^{(i)}; \theta) }$$

The principal of Maximum Likelihood

앞에서 구축한 확률 모델 $p(\vec{y} \vert X; \theta)$에서 어떤 $\theta$ 값이 가장 합리적일까? 그것은 $p(\vec{y} \vert X; \theta)$의 값을 Maximize하는 $\theta$이다!

“The principle of maximum likelihood says we should choose $\theta$ so as to make the data as high probability as possible. I.e., we should choose $\theta$ to maximuze $L(\theta)$”

Log Likelihood $l(\theta)$

하지만 $L(\theta)$를 바로 Maximize하는 것은 쉽지 않다. Derivative of $L(\theta)$는 상당히 그것을 유도하는 것이 복잡하기 때문이다.

그래서 우리는 $L(\theta)$에 $\log$를 취한 $l(\theta)$를 대신 사용할 것이다!

$$ \begin{split} l(\theta) &= \log {L(\theta)} = \log { p(\vec{y} \vert X; \theta) }\\ &= \log {\prod _{ i } { p(y^{(i)} \vert X^{(i)}; \theta) }} \\ &= \sum_{i} { \log { p(y^{(i)} \vert X^{(i)}; \theta) }} \\ &= \sum_{i} { \log { \frac{ 1 }{ \sqrt{2\pi} \sigma } \textrm{ exp } \left( - \cfrac{ {\left( y^{(i)} - \theta^{T} x^{(i)} \right)}^{2} }{2 \sigma^{2}} \right) } } \\ &= m \log {\frac{ 1 }{ \sqrt{2\pi} \sigma}} - \cfrac{1}{\sigma^{2}} \cdot \cfrac{1}{2} \sum_{i} { {\left( y^{(i)} - \theta^{T} x^{(i)} \right)}^2 } \end{split} $$

$l(\theta)$를 Maximize 하기 위해선 위의 식에서 $- \cfrac{1}{\sigma^{2}} \cdot \cfrac{1}{2} \sum_{i} { {\left( y^{(i)} - \theta^{T} x^{(i)} \right)}^2 }$ 부분을 Maximize 해야 한다.

이때, 음수 부호 $-$를 고려하여 반전하면,

$\cfrac{1}{\sigma^{2}} \cdot \cfrac{1}{2} \sum_{i} { {\left( y^{(i)} - \theta^{T} x^{(i)} \right)}^2 }$를 minimize하는 것이고 이것은 $J(\theta)$를 의미한다!!

---

동치 관계를 정리해보자.

1. $\max{L(\theta)} \equiv \max{l(\theta)}$
2. $\max{l(\theta)} \equiv \max{\sum_{i}{- \frac{\left( y^{(i)} - \theta^{T} x^{(i)} \right)^2}{2{\sigma}^2}}}$
3. $\max{\sum_{i}{- \frac{\left( y^{(i)} - \theta^{T} x^{(i)} \right)^2}{2{\sigma}^2}}} \equiv \min{\frac{1}{2}\sum_{i}{\left( y^{(i)} - \theta^{T} x^{(i)} \right)^2}} = \min{J(\theta)}$
4. $\max{L(\theta)} \equiv \min{J(\theta)}$

참고로 Likelihood Maximizing은 Regression problem 외에도 Classification Problem에서도 적용가능 하다!!

맺음말

결론적으로 우리는 LMS 방식을 사용하면서 Likelihood $L(\theta)$를 Maximizing하고 있었다. 물론 $\textrm{LMS} \equiv \textrm{MLE}$에는 IID라는 가정이 필요하지만, 이 동치 관계는 LMS 방식을 지지하는 강력한 기반을 제공한다.

---

1. $p (y^{(i)} \vert x^{(i)}; \theta )$와 $p ( y^{(i)} \vert x^{(i)}, \theta )$는 분명 다른 의미를 갖는다. ‘$;$’를 사용할 경우 그 의미는 “parameterized by”가 된다. 반면, ‘$,$’를 사용할 경우 “$\theta$에 대해 conditioning 됨”을 의미한다. 이때 $p ( y^{(i)} \vert x^{(i)}, \theta )$는 틀린 표현인데, $\theta$가 random variable이 아닌 parameter의 지위를 갖기 때문이다. ↩