Interpretation of Decision Boundary with Learning
본 글은 2018-2학기 Stanford Univ.의 Andrew Ng 교수님의 Machine Learning(CS229) 수업의 내용을 정리한 것입니다. 지적은 언제나 환영입니다 :)
Decision Boundary
Linear Classification은 Feacture Space 위의 두 Class를 나누는 Decision Boundary를 만든다. 이번에는 이 Decision Boundary에 대한 이야기를 풀어나가고자 한다.
Feacture Space & Decision Boundary(=Hyperplain)
먼저 Feacture Space에 대해 정의해보자. 이것은 $x$가 존재하는 공간이다. 만약 $x \in \mathbb{R}^{n}$이라면, Feacture Space는 $\mathbb{R}^{n}$의 공간이 되면, $x$는 Feacture Space 상의 한 점이 된다.
아래와 같은 그림을 상상하면 된다. 1

이때, Decision Boundary는 Feacture Space 상의 두 Class를 나누는 Hyperplain이다. 2
공간 상에서 평면을 어떻게 정의하는지 곱씹어 보자.
2가지 요소가 필요한데,
- 평면이 지나는 한 점 $P_0$
- 그 점을 지나는 Normal vector $\vec{w}$
가 필요하다.
평면에 대한 식은 $\vec{w} \cdot x + b = 0$으로 표현된다.
그래서 우리가 찾고자 하는 Hyperplain Boundary $\vec{w} \cdot x + b = 0$를 얻기 위해선, 두 Class를 잘 나누는 적절한 $\vec{w}$와 $b$를 찾아야 한다.
Linear Classification
Linear Classification은 $\theta^{T}x$를 통해서 입력 $x$와 parameter $\theta$를 연관짓는다. 이때 $\vec{w} \cdot x + b$는 $\theta^{T}x$의 다른 형태로 기술한 것이다.
앞선 파트에서 우리는 Logistic Regression을 살펴보았고, hypothesis로 $h_{\theta}(x) = \frac{1}{1 + e^{-\theta^{T}x}}$를 사용하였다. sigmoid function 자체는 non-linear 함수이다. 하지만, $\theta$와 $x$가 $\theta^{T}x$라는 Linear한 방식으로 연결되어 있기 때문에 Logistic Regression도 결국은 Linear Classification에 속한다.
참고로 non-Linear Classifier는 $\theta^{T}x$ 대신 $x^2_j$나 ${x_i}{x_j}$를 사용해 Classification을 진행한다.
Interpretation of Decision Boundary with Learning
앞의 문단에서 Linear Classification은 Feacture Space를 분할하는 Hyperplain을 찾는 것임을 살펴보았다. 이번에는 Hyperplain과 Learning의 관계에 대해 살펴보고자 한다.
먼저 $\theta$는 Hyperplain의 Normal vector이다. 그리고 Hyerplain을 기준으로 $\theta^{T}x > 0$이면 악성 종양, $\theta^{T}x < 0$이면 음성 종양으로 해석한다고 해보자.
그러면, Hyperplain은 다음과 같다.
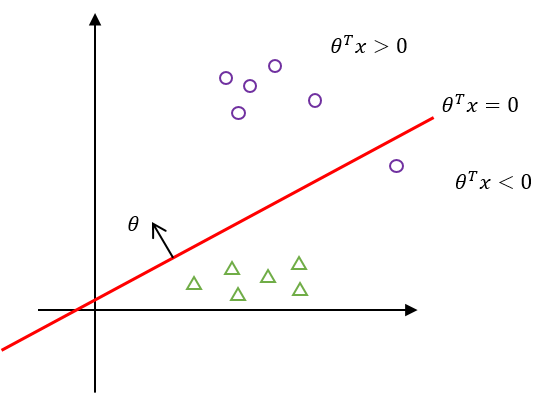
하지만, 이 모델은 하나의 원(○)을 놓치고 있다. 이 특정한 입력 $x_j$에 대해 $\theta$와의 내적값을 확인해보면,
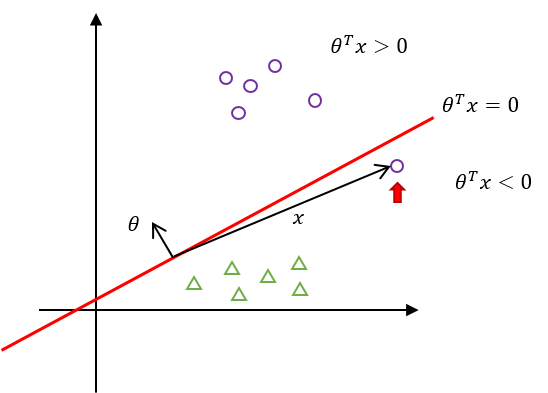
$\theta^{T}{x_j} < 0$이라는 결과가 나온다. 하지만 이것은 본래 $x_j$가 가졌어야 할 $y_j=1$이라는 결과와는 크게 다르다! 그래서 Learning rule을 이용해 $\theta$의 값을 갱신해줘야 한다.
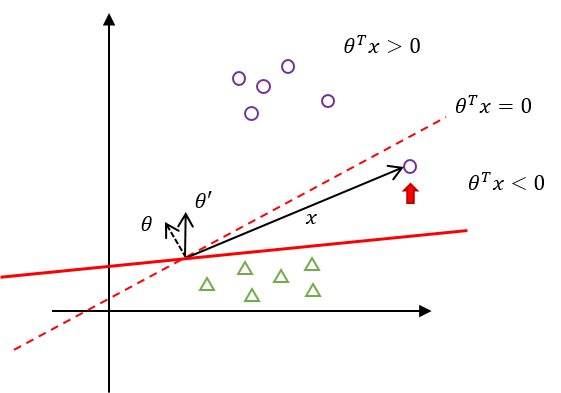
$\theta$를 $\theta’$으로 갱신한 결과, 새로운 Hyperplain이 정의되었다. 이 Hyperplain은 모든 원(○)를 $(\theta’)^T x > 0$로 분류하고 있다.
맺음말
- Linear Classification은 Feacture Space를 Hyperplain으로 나눈다.
- 우리가 본 Logistic Regression도 결국은 Linear Classification에 속한다.
- Linear / non-Linear Classification 여부를 결정하는 것은 parameter $\theta$와 입력 $x$가 어떻게 엮여 있으냐 이다.
- Linear Classification에서 parameter $\theta$는 Hyperplain의 normal vector이다.
- Learning을 통해 $\theta$를 갱신하면 Hyperplain의 기울기가 변화한다.
