Exponential Family, and GLM

본 글은 2018-2학기 Stanford Univ.의 Andrew Ng 교수님의 Machine Learning(CS229) 수업의 내용을 정리한 것입니다. 지적은 언제나 환영입니다 :)

– lecture 4

주의!: 이번 글은 제가 완벽히 이해하지 못한 주제를 다루고 있어, 부족한 점이 많습니다.

---

이번 글에서는 앞에서 살펴본 Linear Regression, Logistic Regression 모델을 전부 포괄하는 일반화된 형태의 Linear Model인 GLM_{Generalized Linear Model}을 살펴본다.

---

(사전 지식) Bernoulli Distribution

이산 확률 분포_{Discrete Probability Distribution}의 일종이다. Binary Classification이 갖는 확률 분포이다. 다음과 같은 형태를 가지며, 이때 $\phi$는 ‘probability of event’이다.

$$p(y; \phi) = \phi^{y} (1-\phi)^{(1-y)}$$

---

The Exponential Family

세상에는 셀수없이 많은_countless Distribution이 존재할 것이다. 하지만 Gaussian 분포와 Bernoulli 분포 같이 인간은 몇몇 Distribution을 수식의 형태로 정형화하고 분석하였다.

그러던 중 Distribution에서 보이는 어떤 ‘패턴‘을 발견하게 되었고, 그 패턴을 가지는 Distribution을 모아 Family라고 불리는 집합을 제시한다. 이번에 다루는 Exponential Family는 그런 특정 패턴을 보이는 확률 분포를 포괄하는 것이다.

확률 분포가 다음과 같은 꼴을 가지면, “확률 분포가 Exponential Family에 속한다.”고 말한다.

$$p(y; \eta) = b(y) \exp{\left( \eta^{T} T(y) - a(\eta) \right)} $$

이때 위의 형태에 등장하는 변수와 함수들은 다음과 같은 이름을 가진다. (외울 정도로 중요하지는 않다.)

• $y$: data
• $\eta$: natural parameter (of distribution)
• $T(y)$: sufficient statistic
• $b(y)$: base measure
• $a(\eta)$: log partition function

준식에 대한 설명을 좀더 들어보자.

$$p(y; \eta) = \frac{b(y) \exp{\left( \eta^{T} T(y) \right)}}{e^{a(\eta)}} $$

• $\eta$는 distribution의 parameter이다. parameter of distribution
• 일반적으로 $T(y)$는 $y$로 설정한다.
• $\eta$는 vector, $T(y)$는 vector function인 반면, $b(y)$와 $a(\eta)$는 scalar function이다.
• $a(\eta)$는 분포를 normalize하는 역할을 한다. $a(\eta)$을 잘 설정함으로써 확률분포의 적분/덧셈값을 1로 만들 수 있다.

지금부터는 Bernoulli 분포와 Gaussian 분포가 Exponential Family에 속함을 살펴볼 것이다!

---

Bernoulli Distribution ∈ Exponential Family

Bernoulli Distribution은 binary data에 대한 확률 분포이다. $\phi$는 probability of event로 Bernoulli Distribution은 아래와 같다.

$$p(y; \phi) = \phi^{y}(1-\phi)^{(1-y)}$$

우리는 위의 Bernoulli Distribution 식에 Algebraic Massage¹를 통해 Bernoulli Distribution이 Exponential Family에 속함을 보일 것이다!

Bernoulli Distribution 식을 다음과 같이 변형해보자.

$$ \begin{split} p(y; \phi) &= \phi^{y}(1-\phi)^{(1-y)} \\ &= \exp{ \left[\log{ \left(\phi^{y}(1-\phi)^{(1-y)}\right) }\right] } \\ &= \exp{ \left[ \left( \log{ \left( \frac{\phi}{1-\phi} \right) } \right)y + \log{(1-\phi)} \right] } \end{split} $$

위 식에서 $\eta$, $T(y)$, $a(\eta)$, $b(y)$를 찾아보면

• $\eta$: $\log{(\phi / (1-\phi))}$
• $T(y)$: $y$
• $a(\eta)$: $-\log{(1-\phi)}$
  • 이때 $\eta = \log{(\phi / (1-\phi))}$임을 이용해 $\eta$에 대한 식으로 다시 쓰면,
  • $\phi = 1/(1+e^{-\eta})$
  • $a(\eta) = \log{(1+e^{\eta})}$
• $b(y)$: $1$

즉, 기존의 Bernoulli Distribution을 적절히 변형해서 $\eta$, $T(y)$, $a(\eta)$, $b(y)$를 잘 설정해줌으로써 Bernoulli Distribution이 Exponential Family에 속함을 보였다!

---

Gaussian Distribution ∈ Exponential Family

이번에는 Gaussian Distribution이 Exponential Family에 속함을 살펴보자. 이때, Variance $\sigma^{2}$는 어떤 함수가 아니라 고정되어 있다. 여기에서 우리는 $\sigma^{2}$가 $1$이라고 가정한다.

Gaussian Distribution의 식은 아래와 같다.

$$ \begin{split} p(y; \mu) &= \frac{1}{\sqrt{2\pi}\sigma} \exp{\left( - \frac{(y-\mu)^2}{2\sigma^{2}} \right)} \\ &= \frac{1}{\sqrt{2\pi}} \exp{\left( - \frac{(y-\mu)^2}{2} \right)} \end{split} $$

이제 위 식을 적절히 Algebraic Massage 할 것이다.

$$ \begin{split} p(y; \mu) &= \frac{1}{\sqrt{2\pi}} \exp{\left( - \frac{(y-\mu)^2}{2} \right)} \\ &= \frac{1}{\sqrt{2\pi}} \exp{\left(-\frac{y^2}{2}\right)} \cdot \exp{\left(\mu y - \frac{1}{2} {\mu^{2}} \right)} \end{split} $$

위 식에서 $\eta$, $T(y)$, $a(\eta)$, $b(y)$를 찾아보면

• $\eta$: $\mu$
• $T(y)$: $y$
• $a(\eta)$: $\mu^{2} / 2 = \eta^{2} / 2$
• $b(y)$: $(1/\sqrt{2\pi})\exp{(-y^{2} / 2)}$

즉, 기존의 Gaussian Distribution을 적절히 변형해서 $\eta$, $T(y)$, $a(\eta)$, $b(y)$를 잘 설정해줌으로써 Gaussian Distribution이 Exponential Family에 속함을 보였다!

지금까지 살펴본 Bernoulli Distribution, Gaussian Distribution 외에도 많은 확률 분포들이 Exponential Family에 속한다.²

---

Generalized Linear Model

지금부터 우리는 일반적인 형태의 Regression과 Classification 문제를 어떻게 모델링 하는지에 대해 다룰 것이다. 우리는 주어진 상황을 $x$로 두고, random variable $y$를 function of $x$로 둘 것이다. 그리고 우리는 $x$에 대한 $y$의 확률 분포를 예측할 것이다.

GLM을 모델링 할 때 우리는 다음의 3가지를 가정한다.

1. $y \vert x; \theta \sim \textrm{ExponentialFamily}(\eta)$
   즉, 주어진 $x$, $\theta$에 대한 $y$의 확률 분포가 $\eta$를 파라미터로 하는 Exponential family의 확률분포를 따른다.
2. natural parameter $\eta$와 input $x$는 linearly related 되어 있다: $\eta = \theta^{T} x$
3. 우리는 학습을 통해서 prediction $h(x)$가 $\textrm{E}[y \vert x; \theta]$를 만족하도록 할 것이다³: $h(x) = \textrm{E}[y \vert x; \theta]$

위의 3가지 가정들, 또는 Design choice를 통해서 우리는 훌륭한 Generalized Linear Model을 얻게 된다. GLM이 중요한 이유는 GLM이 Learning에서 유용한 여러 성질들을 가지고 있기 때문이다!

---

상황을 그림으로 이해해보자.

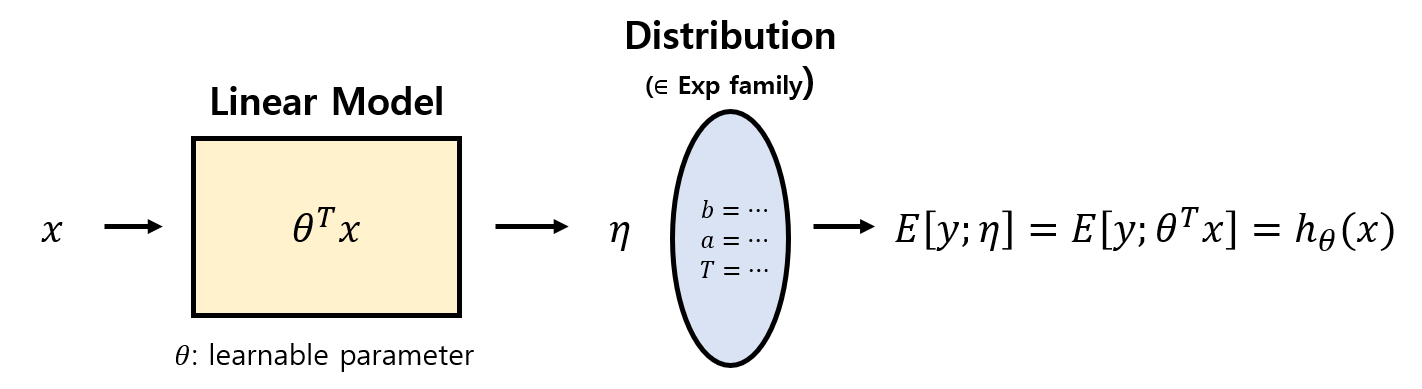
• 가정(2)에 따라 $\eta=\theta^{T}x$이므로 $\eta$는 Linear Model의 출력값이다.
• 입력 데이터와 목적에 따라 적절한 Distribution을 디자인 한다. = 적절한 $a$, $b$, $T$를 정한다.

이번엔 Training/Test Phase에서 모델이 어떻게 작동하는지를 살펴보자.

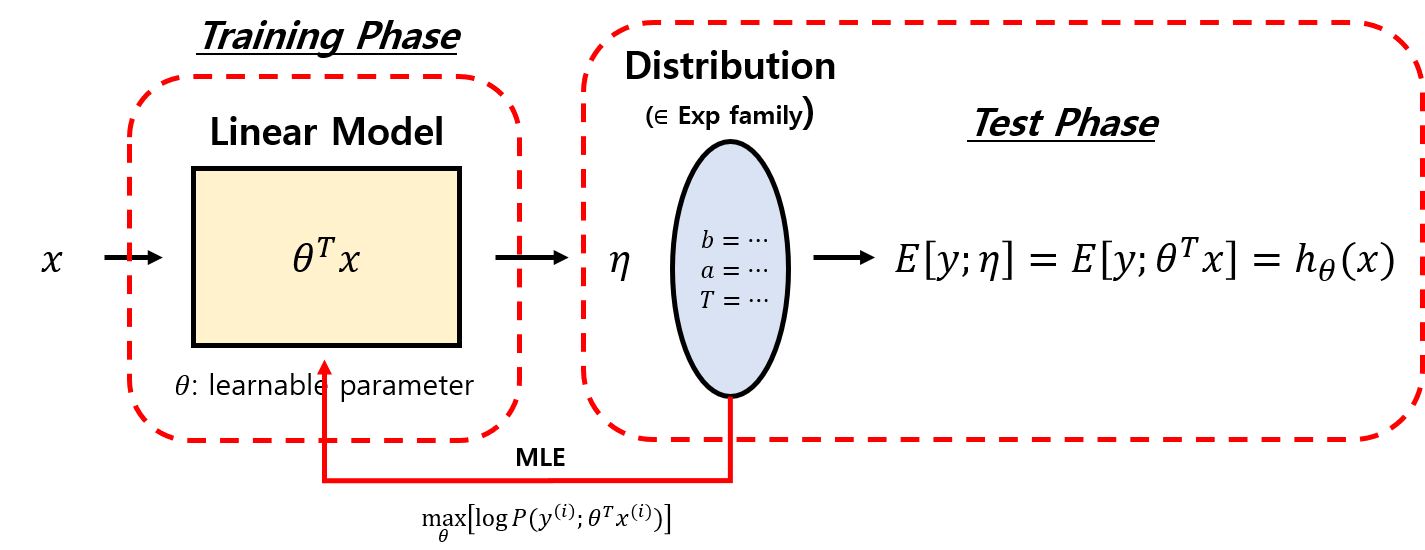
• Training에서 영향을 받는 것은 오직 Linear Model이다. Distribution은 전혀 영향이 없으며, Learning의 대상이 아니다.
• 우리는 Distribution의 출력값으로 Test를 진행한다.
  • Distribution의 출력으로 평균값인 $\textrm{E}[y \vert x ; \theta]$를 얻고, 가정(3)에 따라 그것은 $h_{\theta}(x)$이다.
  • Distribution의 출력은 정답 $y$와 비교되어 $\theta$ 값을 갱신하는 지표로 사용된다.

---

Ordinary Least Squares

지금까지 제시한 GLM의 원리를 GLM의 특수한 경우 중 하나인 Ordinary Least Squares를 살펴봄으로써 곱씹어 보자.

예측하고자 하는 target variable $y$(GLM에서는 response variable이라고도 함.)가 연속적이고, Gaussian $\mathcal{N}(\mu, \sigma^{2})$를 만족한다고 가정할 것이다.

Gaussian은 Exponential Family에 속하므로, Gaussian의 파라미터 $\mu$는 Exponential Family의 $\eta$가 된다. : $\mu = \eta$

그리고 Ordinary Least Squares에서 설정한 hypothesis $h_{\theta}(x)$는 다음과 같이 유도된다.

$$ \begin{split} h_{\theta}(x) &= \textrm{E}[y \vert x ; \theta] \\ &= \mu \\ &= \eta \\ &= \theta^{T}x \end{split} $$

각 과정에 대한 자세한 설명을 들어보자.

• $h_{\theta}(x) = \textrm{E}[y \vert x ; \theta]$는 3번째 가정을 통해 제시된다.
• $\textrm{E}[y \vert x ; \theta] = \mu$는 $y \vert x ; \theta \sim \mathcal{N}(\mu, \sigma^{2})$임을 통해 제시된다.
• $\mu = \eta$는 Gaussian의 파라미터를 Exponential Family의 파라미터로 변환한 것이다.
• $\eta = \theta^{T}x$는 2번째 가정을 통해 제시된다.

Relation btw three parameters

위에서 나온 $\mu$를 canonical parameter라고 부른다. canonical parameter는 Regression의 목적에 따라 설계한 Distribution이 갖는 변수이다. 예를 들어 Bernuolli Distribution에서는 $\phi$가 canonical parameter이다.

cononical parameter $\mu$와 natural parameter $\eta$에 대한 관계는 canonical response function $g(\eta)$으로 표현된다. 그리고 canonical function의 inverse는 canonical link function $g^{-1}(\mu)$로 표현된다.

$$\mu = \textrm{E}[y; \eta] = g(\eta)$$ $$\eta = g^{-1}(\mu)$$

model parameter $\theta$, natural parameter $\eta$, canonical parameter $\mu$ or $\phi$, canonical function $g(\eta)$, $g^{-1}(\mu)$에 대한 관계를 다이어그램으로 표현하면 다음과 같다.

Logistic Regression을 예로 들어 살펴보자!

$$ \begin{split} h_{\theta}(x) &= \textrm{E}[y \vert x; \theta] \\ &= \phi = g(\eta) = \frac{1}{1+e^{-\eta}} = \frac{1}{1+e^{-{\theta^{T}x}}} \end{split} $$

놀랍게도 지금까지 GLM에서 살펴본 흐름이 Logistic Regression의 결과에 그대로 녹아있었다.

결국 sigmoid function은 그냥 나온 것이 아니라 Bernoulli Distribution을 GLM으로 해석하여 유도한 결과인 것이다.

---

맺음말

GLM을 살펴봄으로써 지금까지 행해왔던 Linear Regression 모델의 패러다임을 엿볼 수 있었다. Linear Regression과 Logistic Regression 로는 세상의 모든 문제를 해결할 수 없다. 앞으로 더 복잡하고 정교한 Regression을 학습하고 사용하게 될 텐데, 그때의 Regression Model이 GLM의 패러다임을 바탕으로 하고 있음을 인지한다면 본 글을 잘 이해한 것이다.

GLM을 요약해보자.

• 우리가 Regression에서 쓰는 대부분의 모델은 Exponential Family에 속한다.
• GLM은 Exponential Family에 속하는 확률 분포를 갖는 모델의 패턴을 정리한 것이다.
• GLM은 Linear Model과 우리가 디자인한 Distribution이 어떻게 연결되어야 하는지를 말해준다.
  • Logistic Regression의 경우, Bernoulli 분포를 Exponential Family의 형태로 바꿈으로써 $\theta^{T}x$와 확률 $\phi$를 연결하는 sigmoid 함수를 찾을 수 있었다.

---

1. lecture 강연자가 사용한 말인데, 정말 마음에 든다!!! Algebraic Massage는 확률 분포 식의 형태를 변형한다는 말이다. ↩

2. Poisson Distribution, Gamma Distribution, Drichlet Distribution 등등… ↩

3. 본래의 목표은 $T(y)$의 평균_{expected value}를 구하는 것이지만, 대부분의 경우 $T(y)=y$로 두기 때문에, 우리는 $\textrm{E}[y \vert x; \theta]$를 구하는 것을 목표로하게 된다. ↩