Multi-class Classification
본 글은 2018-2학기 Stanford Univ.의 Andrew Ng 교수님의 Machine Learning(CS229) 수업의 내용을 정리한 것입니다. 지적은 언제나 환영입니다 :)
Multi-class Classification
지금까지의 Classification Problem은 $y \in \{0, 1\}$의 Binary Classification이었다. 이번에는 $y \in \{1, 2, …, k\}$의 Multi-Class Classification에 대해 살펴볼 것이다.
(사전지식) Multinomial Distribution
이번 글을 이해하기 위해선 Multinomial Distribution를 먼저 이해할 필요가 있다.
우리는 이미 ‘-nomial’이 붙은 단어를 하나 알고 있다. 바로 Bi-nomial이다. Binomial Distribution은 이항분포로, $N$번의 동전 던지기에서 앞/뒷면이 몇번 나올지에 대한 분포를 떠올리면 된다. 이항분포는 $B(n, p)$로 표현하며 $n$는 시행횟수, $p$는 기준이 되는 event의 확률이다.
이항분포에서 $n$번 시행 중 $k$번 성공할 확률은 다음과 같다.
그리고 이항계수 $\binom{n}{k}$는 아래와 같이 표현된다.
이항분포의 상황을 Multi-class로 확장하면, 다항분포, Multinomial이 된다.
$k$개 카테고리에 그 값들이 나타날 확률을 각각 $p_1$, $p_2$, …, $p_k$라고 하자. $n$번의 시행에서 $i$번째 값이 $x_i$회 발생할 확률은 다음과 같다.
Multinomial Distribution에서는 표본값이 벡터 $\vec{x}=(x_1, \ldots, x_k)$가 된다. 즉, 주사위를 10번 던져 주사위 눈의 출현 횟수가 $(3, 2, 3, 1, 1, 0)$일 확률을 Multinomial Distribution을 통해 얻을 수 있는 것이다.
다항분포에서의 계수도 이항분포의 이항계수 $\binom{n}{k}$와 같이 표현할 수 있다.
Multi-Class Classification with GLM
Multi-Class Classification Problem을 GLM의 꼴로 기술해보자.
먼저 $T(y)$를 다음과 같이 정의할 것이다.
그리고 $(T(y))_i$는 벡터 $T(y)$의 i번째 원소를 가리킨다.
이때 편의를 위해 마지막 클래스인 $k$를 다른 $k-1$의 클래스로 유도되는 클래스로 정의하자. 그 말은 곧 $T(y)$를 다음과 같이 정의하자는 것이다.
이것을 통해 벡터 $T(y)$의 차원을 $\mathbb{R^{k-1}}$로 줄일 수 있다. 그리고 $k$의 확률 $p(y=k;\phi)$는 $1 - \sum_{i=1}^{k-1} {\phi_i}$로 정의한다.
이번엔 각 class 별로 parameter $\theta_{i} \in \mathbb{R}^n$를 정의할 것이다.
그래서 전체 class의 parameter를 모은 $\theta$는 $\mathbb{R}^{n \times k}$의 행렬이 된다.
우리는 또 하나의 새로운 표기법을 도입한다. indicator function $1 \{ \cdot \}$은 괄호 안의 명제가 참이라면 1을, 거짓이라면 0을 반환하는 함수이다. 그래서 $1\{\textrm{True}\}$는 $1$이고, $1\{\textrm{False}\}$는 $0$이다.
이것을 활용해 확률 $p(y; \phi)$를 다음과 같이 표현한다.
이제 $p(y; \phi)$에 Algebraic Massage를 해보면,
이제 GLM의 각 요소들을 확인해보면,
- $\eta$: $\left[ {\log{(\phi_1/\phi_k)}, \log{(\phi_2/\phi_k)}, \cdots, \log{(\phi_{k-1}/\phi_k)}} \right]^{T}$
- $a(\eta)$: $-\log{(\phi_k)}$
- $b(y)$: $1$
가 된다.
$\eta = \left[ {\log{(\phi_1/\phi_k)}, \log{(\phi_2/\phi_k)}, \cdots, \log{(\phi_{k-1}/\phi_k)}} \right]^{T}$라는 사실에 의해 natural parameter $\eta$와 canonical parameter $\phi$를 연결짓는 link function은 다음과 같이 정의된다.
이번엔 link function의 역함수를 취해 response function을 살펴보자.
따라서 $\phi_k = 1/{\sum_{i=1}^{k}{e^{\eta_i}}}$를 의미하고, 이것을 이용해 $e^{\eta_i} = \frac{\phi_i}{\phi_k}$를 다시쓰면
가 된다. $\eta$를 $\phi$로 매핑하는 이 함수를 우리는 softmax function이라고 한다!
이제 이 softmax function을 이용해 확률 $p(y=i \vert x; \theta)$를 다시 정의해보자.
이 과정에서 GLM의 가정인 “natural parameter $\eta$ and model parameter $\theta$ are linearly related”를 적용하였다.
이렇게 softmax function을 response function으로 사용하는 regression을 softmax regression이라고 한다. softmax regression은 logistic regression의 general model이다.
이제 우리의 최종적인 출력값인 hypothesis $h_{\theta}(x)$를 살펴보자. GLM에서 $h_{\theta}(x)$는 가정에 의해 $\textrm{E}[T(y) \vert x; \theta]$이다.
위의 식에서는 $i=1, \ldots, k-1$에서의 $p(y=i \vert x; \theta)$만을 다루고 있다. $p(y=k \vert x; \theta)$의 경우는 $1-\sum_{i=1}^{k-1} {\phi_i}$로 얻을 수 있다.
Cross Entropy
앞에서 다룬 Softmax Regression을 그림을 통해 복습하면서 Softmax Regression의 Loss function인 Cross Entropy에 대해 살펴보자.
우리는 $\theta$와 linearly related 된 $\eta$에 exponential과 normalize를 취하여 predicted probability인 $\hat{p}(y)$을 유도하였다.
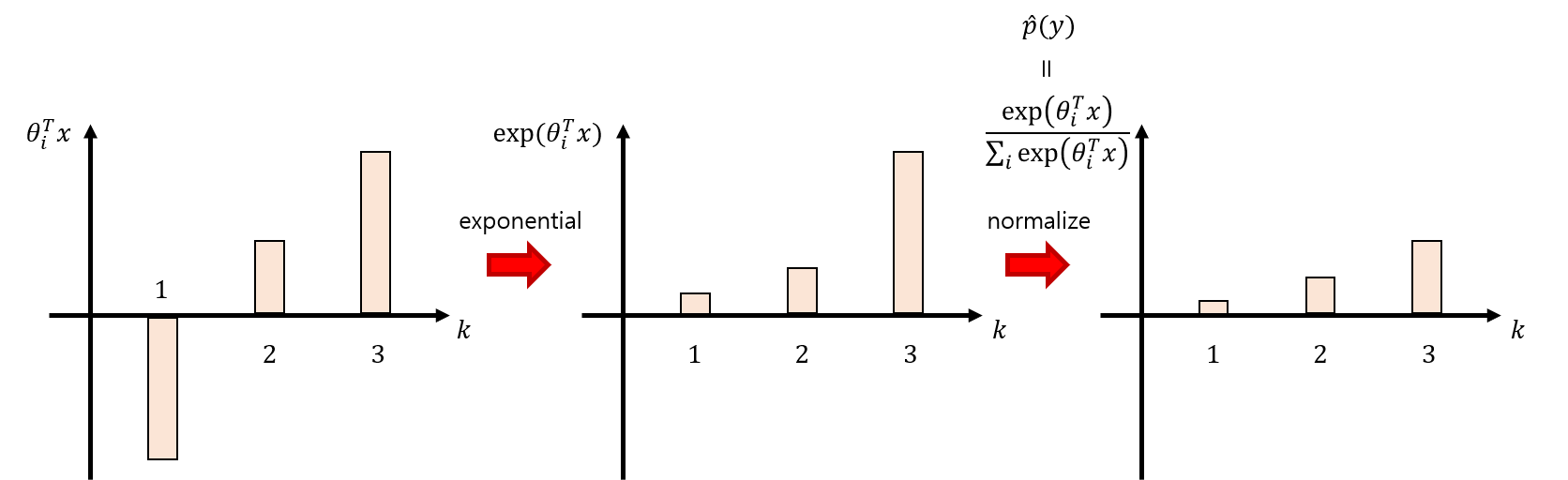
하지만 $\hat{p}(y)$은 엄연히 predicted 값일 뿐! 우리는 $\hat{p}(y)$과 실제 값인 $p(y)$를 비교하여 둘 사이의 오차를 최소화 해야 한다. 이때 정답 레이블에 대해 $p(y)$는 $1$의 값을 가진다.
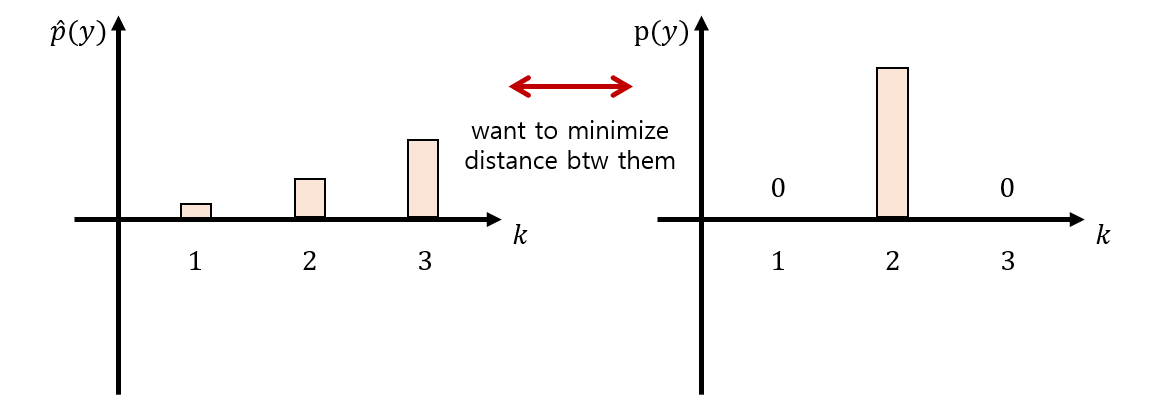
이제 $\hat{p}(y)$와 $p(y)$ 사이의 오차를 최소화하는 지표인 Cross Entropy가 등장한다. Cross Entropy는 다음과 같이 정의된다.
이때 $p(y)$의 값은 정답 레이블에 대해서만 $1$의 값을 갖기 때문에, $\textrm{CrossEnt}(p, \hat{p})$은 다음과 같이 기술된다.
그리고 우리가 앞선 과정에서 구한 $\hat{p}(y_i)$의 식을 대입하면,
이제 parameter $\theta$를 업데이트하고자 한다면, 위의 $\textrm{CrossEnt}(p, \hat{p})$에 Gradient Descent 방법을 취함으로써 Softmax Regression Model을 최적화할 수 있다!
맺음말
본 글에서는 Multi-class Classification을 GLM의 관점에서 살펴보았다. 내용을 요약하면 다음과 같다.
- Multi-class Classification은 Multinomial에서 출발한다.
- softmax function 함수는 $\eta$를 $\phi$로 매핑하는 response function이다.
- Cross Entropy는 정답 레이블 $p(y)$과 softmax function으로 얻은 predicted probability $\hat{p}(y)$ 사이의 오차를 정의하는 함수이다.
