Generative Learning Algorithm, and GDA
본 글은 2018-2학기 Stanford Univ.의 Andrew Ng 교수님의 Machine Learning(CS229) 수업의 내용을 정리한 것입니다. 지적은 언제나 환영입니다 :)
GDA(Gaussian Discriminant Analysis)라는 기법이 등장한다. 이름이 후덜덜 하게 생겼지만, 이론은 별거 없다. 안심하고 다이브🤿하자!
Generative Learning Algorithm
우리가 살펴본 Logistic Regression 모델들은 Discriminative Learning에 속하는 모델이었다.
Discriminative 모델에서는 $p(y \vert x)$를 학습하는 것을 목표로 한다. 반면에 Generative 모델은 $p(x \vert y)$와 $p(y)$를 학습하는 것을 목표로 한다.1
Generative Learning은 Bayes Rule을 바탕으로 하는 이론이다.
우리가 목표로 하는 것은 여전히 $p(y \vert x)$이다. Discriminative 모델은 $p(y \vert x)$를 학습하는 반면, Generative 모델은 $p(x \vert y)$와 $p(y)$를 정의하고 학습하여 $p(y \vert x)$의 값을 간접적으로 유도한다. 구체적으로는 다음과 같다.
결국 Discriminative나 Generative나 큰 흐름은 동일하지만, 구하는 과정이 direct이나 indirect이나의 차이일 뿐이다.
(사전지식) Bayes Rule
Bayes Rule의 용어를 정리해보자.
- $p(y \vert x)$: posterior probability
- 데이터 X에 대한 레이블 Y의 확률이다.
- Classification의 기준이 된다.
- $p(y)$: prior probability
- 정답 레이블의 분포를 통해 얻는다.
- 레이블 y의 수 / 전체 데이터 수
- $p(x \vert y)$: likelihood
- 레이블 Y를 갖는 데이터의 분포를 의미한다.
- Generative Model은 이 확률을 모델링하고 또 학습한다.
- $p(x)$
- 보통 값을 구할 수도 없고, 구할 필요도 없다.
- 그래서 잘 신경 쓰지 않는다.
분류 문제를 기준으로 말하자면, Logistic Regression이 Discriminative Model에 속한다. Naive Bayes Classifier는 Generative Model에 속한다. 또 아래에 언급되는 GDA(Gaussian Discriminant Analysis)도 Generative Model이다.
Gaussian Discriminant AnalysisGDA
GDA는 이름에 ‘Discriminant’가 들어가지만, Generative Model이다. GDA에서는 $p(x \vert y)$가 multivariate normal distribution을 만족한다고 ‘가정’한다. GDA에 대해 본격적으로 다루기 전에 multivariate normal distribution을 가볍게 살펴보자.
(사전지식) Multi-variate normal distribution
바탕이 되는 uni-variate Gaussian 분포를 먼저 살펴보자.
- $E[x]=\mu$
- $\textrm{Cov}(x) = E[(x-\mu)^2]$
이제 multivariate Gaussian 분포의 경우를 살펴보자. multivariate Gaussian의 경우 평균은 mean vector $\mu \in \mathbb{R}^n$로, 분산은 공분산Covariance라는 이름으로 covariance matrix $\Sigma \in \mathbb{R}^{n \times n}$으로 표현된다.
이때, $\lvert \Sigma \rvert$는 Covariance Matrix $\Sigma$의 determinant 값이다. 그리고 평균과 공분산에 대한 식은 다음과 같다.
- $E[X] = \int_{x}{x p(x; \mu, \Sigma) dx}$
- $\textrm{Cov}(X) = E[(X-E[X])(X-E[X])^{T}]$
- $\mu$가 zero-vector(=zero mean)이고 $\Sigma = I$(=identity covariance)인 경우를 standard normal distribution이라고 한다.
GDA Modeling
binary classification 문제를 GDA로 모델링 하기 위해 다음과 같은 가정을 한다.
- $y \sim \textrm{Bernoulli}(\phi)$
- 이 부분은 가정이 아니다. 이진 분류 문제라서 $y$는 베르누이 분포일 수 밖에 없다.
- $\phi = 0.5$라면 uniform distribution이 될 것이다.
- 참고로 $y$에 대한 분포는 어떤 문제를 푸는지에 따라 자동으로 결정되기 때문에 가정을 도입하는 부분이 아니다.
- $x \vert y = 0 \sim \mathcal{N}(\mu_0, \Sigma)$
- $x \vert y = 1 \sim \mathcal{N}(\mu_1, \Sigma)$
분포를 식으로 기술하면 아래와 같다.
- $p(y) = \phi^y (1-\phi)^{(1-y)}$
- $p(x \vert y=0) = \frac{1}{\sqrt{2\pi}{\lvert \Sigma \rvert}^{1/2}}\exp{\left[ -\frac{1}{2}(x - \mu_0)^{T}\Sigma^{-1}(x-\mu_0) \right]}$
- $p(x \vert y=1) = \frac{1}{\sqrt{2\pi}{\lvert \Sigma \rvert}^{1/2}}\exp{\left[ -\frac{1}{2}(x - \mu_1)^{T}\Sigma^{-1}(x-\mu_1) \right]}$
우리의 GDA 모델의 parameter를 정리하면 다음과 같다.
- $\phi \in \mathbb{R}$
- $\mu_0, \mu_1 \in \mathbb{R}^n$
- $\Sigma \in \mathbb{R}^{n \times n}$ 2
우리는 위의 $\phi$, $\mu_0$, $\mu_1$, $\Sigma$를 학습시킬 것이다!
Joint Likelihood $L(\phi, \mu_0, \mu_1, \Sigma)$를 정의해보자.
잠시 Discriminant Learning에서의 Conditional Likelihood와 비교해보자.
parameter의 측면에서 $\theta$와 $\phi$, $\mu_0$, $\mu_1$, $\Sigma$로 차이가 있고, Maximize 대상도 Discriminant Learning의 경우 $p(y \vert x)$를 Maximize하는 반면 Generative Learning은 $p(x \vert y)p(y)$를 Maximize하고 있다.
MLE on GDA
정의한 $L(\phi, \mu_0, \mu_1, \Sigma)$를 Maximize 하자. 이때, $L(\phi, \mu_0, \mu_1, \Sigma)$에 $\log$를 취한 $l(\phi, \mu_0, \mu_1, \Sigma)$를 대신 Maximize한다.
$l$을 Maximizing 하는 parameter의 값은 다음과 같다. 강의에서도 유도 과정은 생략하였다. (아마 parameter 하나 잡고 미분해서 유도할 듯?)
- $\phi = \frac{\sum_{i=1}^{m} {y^{(i)}}}{m} = \frac{\sum_{i=1}^{m} {1\{y^{(i)}=1\}}}{m}$
- $\mu_0 = \frac{\sum_{i=1}^{m} { 1\{y^{(i)}=0\} x^{(i)} }}{\sum_{i=1}^{m} {1\{y^{(i)}=0\}}}$
- $\mu_1 = \frac{\sum_{i=1}^{m} { 1\{y^{(i)}=1\} x^{(i)} }}{\sum_{i=1}^{m} {1\{y^{(i)}=1\}}}$
- $\Sigma = \frac{\sum_{i=1}^{m} {(x^{(i)} - \mu_{y^{(i)}})(x^{(i)} - \mu_{y^{(i)}})^{T}}}{m}$
$\mu_0$을 잘 살펴보자. $\mu_0$의 결과를 말로 풀어쓰면, “$y=0$인 feacture vector들의 합을 $y=0$의 수로 나눈 것” 즉, 평균이다!! 이 결과는 $\mu_0$가 $y=0$인 정답에 대한 평균이라는 정의와도 의미가 통한다.
이 결과를 그래프로 표현하면 다음과 같다.
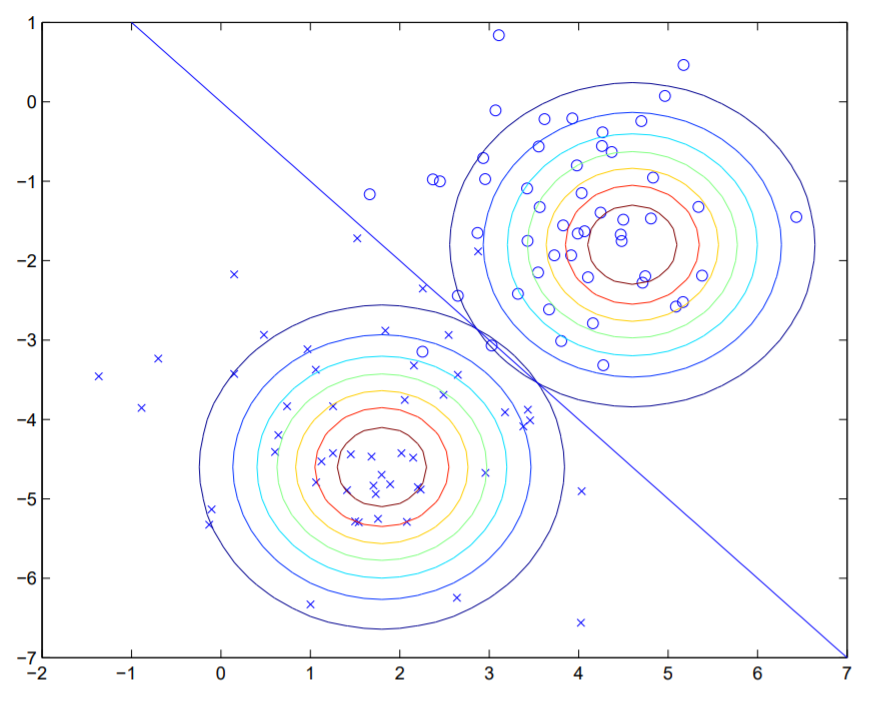
위 그림에 그려진 직선은 $p(y=1 \vert x)=0.5$가 되는 decision boundary의 역할을 한다!!
MLE의 결과를 통해 우리는 $\phi$, $\mu_0$, $\mu_1$, $\Sigma$의 정확한 값을 얻게 되었다. 이 parameter들을 활용해 prediction 할 수 있다.
GDA vs. Logistic Regression
고정된 $\phi$, $\mu_0$, $\mu_1$, $\Sigma$에 대해 $p(y=1 \vert \phi, \mu_0, \mu_1, \Sigma)$를 $x$의 함수로 그려보자.
그러면,
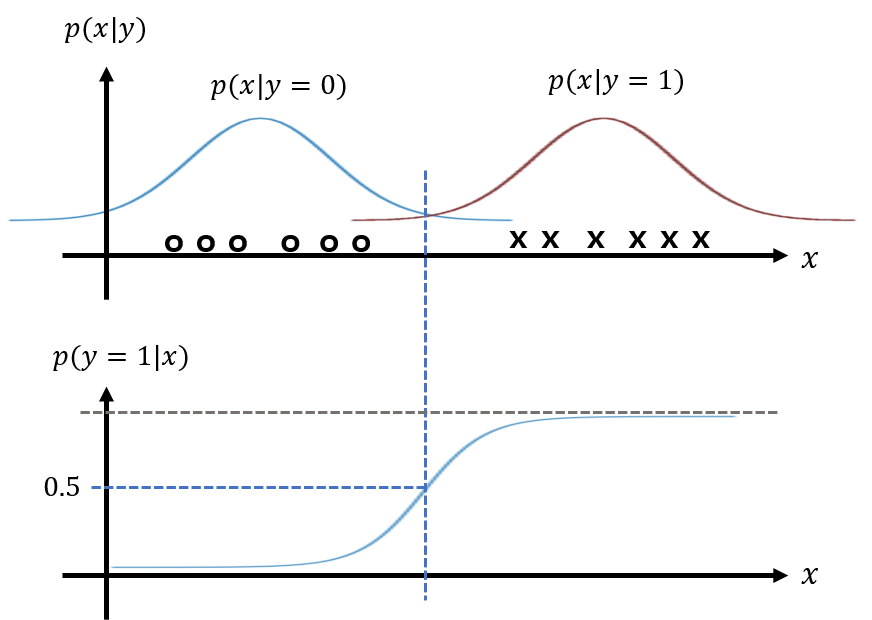
즉, $p(y=1 \vert \phi, \mu_0, \mu_1, \Sigma)$는 sigmoid의 shape이 나온다!!
위의 사실은 GDA와 Logistic Regression이 본질적으로 동일하다는 것을 말한다. 그렇다면 우리는 언제 GDA를 쓰고, 언제 Logistic Regression을 써야 할까??
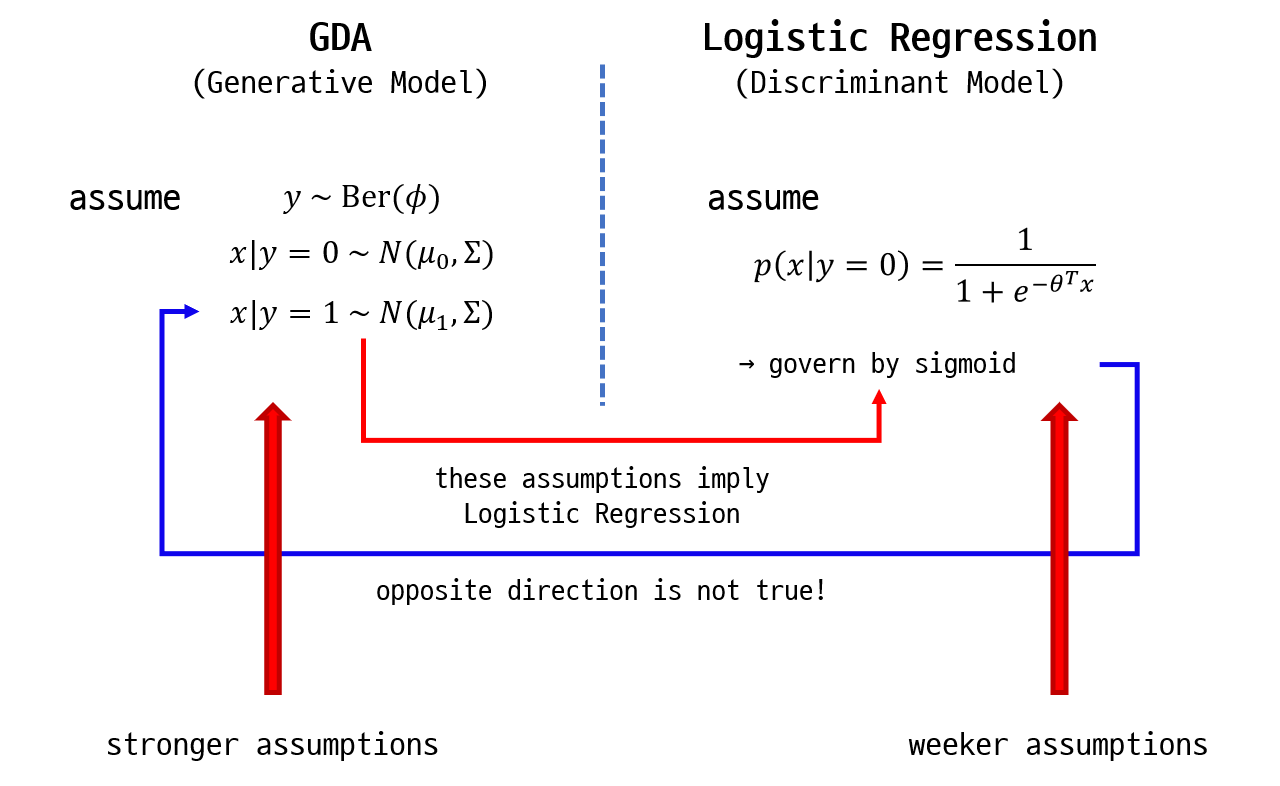
GDA에서 하는 가정들은 Logistic Regression에서 하는 hypothesis $h_{\theta}(x)$의 sigmoid 가정보다 더 강력하다. 그래서 GDA는 Logistic Regression을 암시(imply)한다. 그러나 반대 방향은 불가능하다. 즉, $p(y \vert x)$이 sigmoid라고 해서 $p(x \vert y)$가 multivariate normal distribution인 것은 아니다.
GDA는 더 강력한 가정을 사용하기 때문에 현실의 dataset이 그 가정을 만족하지 않는다면, 안 좋은 성능을 보인다. 그래서 dataset의 분포를 정확히 알고 있다면, GDA로 접근할 수 있지만 그렇지 않다면 Logistic Regression의 방법을 사용하길 권장한다. Logistic Regression은 더 적은 가정을 채용하는 대신에 더 robust 하고 잘못된 모델링에 덜 민감하기 때문이다.
일반적으로 Logistic Regression과 비교했을 때, GDA는 small dataset에서 더 좋은 결과를 낸다고 한다. 반면, huge dataset에서는 Logistic Regression이 더 좋은 결과를 낸다. 단, 만약 $p(x \vert y)$에 대한 GDA의 가정이 옳다면, huge dataset에서도 GDA가 더 좋은 결과를 낸다.
요즘은 CIFAR, ImageNet과 같은 huge dataset이 잘 구축되어 있어, Logistic Regression이 더 강세를 보인다. 그러나 dataset이 잘 구축되지 않았거나 dataset의 크기를 100개로 제한한 상황이라면, GDA가 더 좋은 결과를 낼 수 있다.
