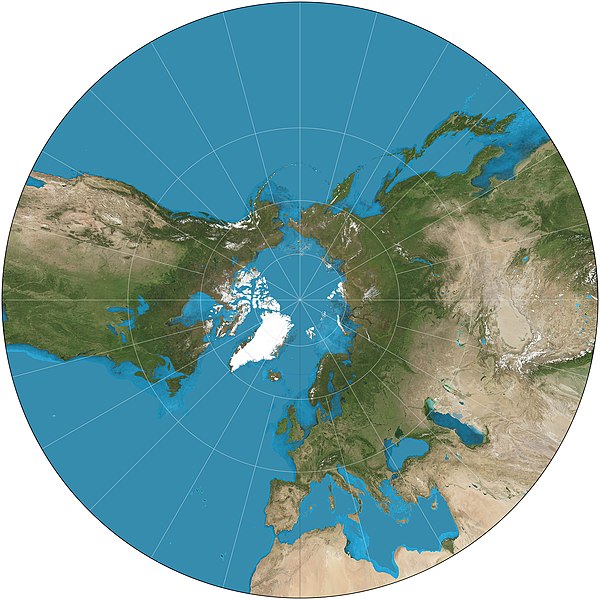
Gnomonic Projection & FOV

본 글은 360 이미지를 2차원에 매핑하는 방식인 Gnomonic Projection(심사도법)에 대해 정리한 글 입니다. 지적은 언제나 환영입니다 :)

표기: longitude는 $\theta \in [-\pi, \pi]$로, latitude는 $\phi \in [-\pi/2, \pi/2]$로 표기하겠습니다.

---

Gnomonic Projection

By Strebe - Own work, CC BY-SA 3.0, Link

360 이미지를 2차원에 매핑하는 대표적인 기법인 Gnomonic Projection에 대해 살펴보자. Gnomonic Projection을 번역하면 심사도법(心射圖法)이라고 한다. 때때로 Gnomonic Projection을 Rectilinear Projection이라는 이름으로 부르기도 한다.

Gnomonic Projection에서 주의할 점은 반구 하나의 범위만을 매핑할 수 있다는 것이다. 즉, 반구 이상의 범위는 Gnomonic Projection으로 매핑할 수 없다.

Azimuthal projection

surface의 기준점에 tangent한 평면을 잡아 projection 하는 방법을 Azimuthal projection이라고 한다. 그래서 Gonomonic projection은 Azimuthal projection의 방법 중 하나이다.

또다른 Azimuthal projection의 예로는 Stereographic projection과 Fisheye projection이 있다.

---

How to map with Gnomonic Projection?

이제 Gnomonic Projection을 어떻게 수행하는지 살펴보자.

먼저 매핑의 중앙에 위치할 점 $S=(\theta_0, \phi_0)$를 정한다.

이제 점 $S$를 기준으로 반구 상의 점들을 매핑해보자.

$$ \begin{aligned} x &= \frac{\cos{\phi} \sin{(\theta - \theta_0)}}{\sin{\phi_0}\sin{\phi} + \cos{\phi_0}\cos{\phi}\cos(\theta-\theta_0)} \\ \\ y &= \frac{\cos{\phi_0}\sin{\phi} - \sin{\phi_0}\cos{\phi}\cos{(\theta-\theta_0)}}{\sin{\phi_0}\sin{\phi} + \cos{\phi_0}\cos{\phi}\cos(\theta-\theta_0)} \end{aligned} $$

위의 공식에서 $x$와 $y$의 분모에 공통적인 부분이 등장한다 이것을 다음과 같이 표현해보자.

$$\cos{c} = \sin{\phi_0}\sin{\phi} + \cos{\phi_0}\cos{\phi}\cos(\theta-\theta_0)$$

$\cos{c}$에서 $c$는 매핑된 평면에서 원점과 $(x, y)$이 이루는 각을 말한다.

공식에서 볼 수 있듯 longitude는 $\theta - \theta_0$를 통해 그 값을 보정하는 반면, latitude $\phi$에는 longitude 같은 보정이 없다. 또한 매핑으로 얻은 $x$와 $y$는 $x^2 + y^2 \le 1$의 unit disk 내부의 점이다.

Inverse mapping

Gnomonic map을 다시 equirectangular의 좌표로 변환하는 방법은 다음과 같다.

$$ \begin{aligned} \phi &= \sin^{-1} {\left( \cos c \sin \phi_0 + \frac{y \sin c \cos \phi_0}{\rho}\right)}\\ \theta &= \theta_0 + \tan^{-1} {\left( \frac{x \sin c}{\rho \cos \phi_0 \cos c - y \sin \phi_0 \sin c} \right)} \\ & \textrm{where, } \rho = \sqrt{x^2 + y^2} \textrm{ and } c=\tan^{-1}{\rho} \end{aligned} $$

공식에서 $(\theta_0, \phi_0) = (0, 0)$으로 설정한다면, gnomonic map은 equirectangular의 중심 부분에 위치하게 된다.

---

Field of View(FOV) & Rectilinear projection

By Hugo Locurcio - Own work, CC0, Link

¹

Field of View, 줄여서 FOV²는 구의 표면을 Gnomonic projection으로 매핑한 범위를 말한다. 통상 FOV는 radian 단위가 아닌 degree 단위로 표기한다.

Gnomonic projection에서 FOV는 최대 180°의 범위를 가질 수 있다. 왜냐하면 Gnomonic projection은 반구 하나 만큼의 영역만 매핑할 수 있기 때문이다.

몇몇 경우에서는 FOV 방식으로 Gnomonic projection을 할 때, Rectilinear projection이라는 표현을 쓴다. 그러나 매핑이 이루어지는 원리 자체는 동일하다. 일반적으로 전체가 아닌 120° 이하의 FOV를 가질 때 Rectilinear projeection이라는 표현을 선호하는 것 같다. 본 글에서는 FOV<=120°인 경우를 특별히 Rectilinear projection으로 지칭하겠다!

Rectilinear projection으로 매핑한 결과는 일반 이미지를 보는 것과 같은 왜곡 없는(undisorted) 이미지를 얻게 된다. 이것은 FOV를 120° 이하로 제한하기 때문에 직선이 직선으로 남게 되기 때문이라고 한다.

By Jelosantisterio - Own work, CC BY-SA 3.0, Link

앞의 Gnomonic projection은 반구를 원형으로 매핑하는 결과를 보여줬다면, Rectilinear projection은 주로 사각형의 이미지로 구의 표면을 매핑한다.

이를 위해 Rectilinear projection은 hFOV와 vFOV³ 값이 필요하다. 이때 hFOV는 longitude $\theta$의 범위를 vFOV는 latitude $\phi$의 범위를 제시한다. 그래서 앞의 Gnomonic projection 공식을 범위와 함께 아래와 같이 다시 쓸 수 있다.

$$ \textrm{for } \theta \in \left[-\frac{\textrm{hFOV}}{2}, \frac{\textrm{hFOV}}{2} \right] \textrm{ and } \phi \in \left[-\frac{\textrm{vFOV}}{2}, \frac{\textrm{vFOV}}{2} \right]\\ \begin{aligned} x &= \frac{\cos{\phi} \sin{(\theta - \theta_0)}}{\sin{\phi_0}\sin{\phi} + \cos{\phi_0}\cos{\phi}\cos(\theta-\theta_0)} \\ y &= \frac{\cos{\phi_0}\sin{\phi} - \sin{\phi_0}\cos{\phi}\cos{(\theta-\theta_0)}}{\sin{\phi_0}\sin{\phi} + \cos{\phi_0}\cos{\phi}\cos(\theta-\theta_0)} \end{aligned} $$

이때의 $x$, $y$의 범위는 $x \in [-\tan{\left(\textrm{hFOV}/2\right)}, \tan{\left(\textrm{hFOV}/2\right)}]$, $y \in [-\tan{\left(\textrm{vFOV}/2\right)}, \tan{\left(\textrm{vFOV}/2\right)}]$가 된다.

inverse mapping에서도 마찬가지로 $x$, $y$의 범위를 제한한 후 매핑하면 equirectangular 상의 영역을 다시 얻을 수 있다.

Cubmap mapping

Cubmap mapping은 구를 6개의 90° FOV 이미지로 매핑하는 방식이다.

매핑의 방식은 Rectilinear projection을 FOV=90°으로 두고 6번을 진행하는 것이기 때문에 자세한 설명을 생략하겠다.

---

맺음말

구의 표면을 2D로 매핑하는 방식은 소개한 Gnomonic projection 외에도 다양한 방법이 존재한다. 하지만 Gnomonic projection의 가장 기본이 되면서 널리 쓰이는 매핑 방식이므로 반드시 숙지해야 한다고 생각한다.

---

참고문헌

• Wolfram MathWorld - Gnomonic Projection
• wiki.panotools - Projections
• wiki.panotools - Rectilinear Projection
• nitishmutha - How to map Equirectangular projection to Rectilinear projection

---

1. 앞의 Gnomonic projection의 구 표면을 외부의 tangent 평면에 매핑을 했다. 이 그림에선 원의 내부에서 구 표면을 바라본다. 그러나 구 표면을 외부에 매핑하는 것과 내부에서 바라보는 것은 완전히 동치인 상황이다! ↩

2. Normal FOV(NFOV)로 표현하는 자료도 있다. ↩

3. wFOV와 hFOV로 표현하는 곳도 있어 혼동하기 쉽다. 이때의 정의는 width FOV, height FOV가 되므로 주의하자! ↩