singular points & poles
2020-2학기, 대학에서 ‘응용복소함수론’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Three Types of (isolated) Singular points
Definition. Principal part of Laurent Series
(i) removable singular point
all $b_n=0$
(ii) poles of order $m$
$b_1 \ne 0$ and $b_n=0$ for $n \ge m+1$ 1
(iii) essential singular point
$b_n \ne 0$ for infinitely many $n$ 2
이중에서 주목할 녀석은 pole이다.
\[\frac{b_1}{(z-z_0)} + \frac{b_2}{(z-z_0)^2} + \cdots \frac{b_m}{(z-z_0)^m}\]점 $z_0$를 pole라고 하며, $m$을 order of pole이라고 한다.
removable singular point
Example. removable singular point
Sol.
$f(z)$에 대한 로랑 급수를 살펴보면, $z=0$이 removable singular point임을 알 수 있다.
$f(z)$의 로랑 급수에 singular point인 $z=0$을 대입하면, $f(0)=\frac{\sin(0)}{(0)}=1$이 된다.
이때, $f(z)$의 극한인 $\underset{z \rightarrow 0}{\lim}{\frac{\sin z}{z}}$ 역시 그값이 $1$이다.
이 결과를 일반화한 정리가 바로 아래의 정리이다.
Theorem.
IF $z_0$ is a removable singular point, THEN $f(z_0)$ is defined & $\underset{z \rightarrow z_0}{\lim} f(z) = f(z_0)$.
그리고 위의 정리를 반대 방향으로 기술하는 정리도 존재한다.
Theorem.
IF $z_0$ is an isolated singular point of $f(z)$ and $f(z)$ is bounded for some neighborhood of $z_0$, THEN $z_0$ is a removable singular point.
$f(z)$의 근방에서 bounded되어 있다는 말은 곧 $\underset{z \rightarrow z_0}{\lim} f(z)$가 존재함을 의미한다. 그리고 이를 통해 $z_0$의 removable을 판단할 수도 있다는 말이다!
poles of order $m$
\[f(z) = \sum^{\infty}_{n=0} {a_n (z-z_0)^n} + \left\{ \frac{b_1}{(z-z_0)} + \frac{b_2}{(z-z_0)^2} + \cdots \right\}\]Definition. simple pole
IF $m=1$, THEN it is called a simple pole.
Example.
Evaluate $\underset{z \rightarrow 0}{\lim} {\lvert f(z) \rvert}$.
Sol.
\(\begin{aligned}
f(z) &= \frac{1}{z^2 (z-1)} \\
&= - \frac{1}{z^2} \frac{1}{1-z} \\
&= - \frac{1}{z^2} (1+z+z^2+\cdots) \\
&= - \frac{1}{z^2} - \frac{1}{z} - 1 - z - \cdots \quad (\lvert z \rvert < 1)
\end{aligned}\)
따라서 $z=0$는 order $2$의 pole이다.
이때, $\underset{z \rightarrow 0}{\lim} {\lvert f(z) \rvert}$는 음수 차수 텀에 의해
\[\underset{z \rightarrow 0}{\lim} {\lvert f(z) \rvert} = \infty\]즉, $\underset{z \rightarrow 0}{\lim} {\lvert f(z) \rvert}$가 bounded 되어 있지 않으므로 $z=0$는 removable이 아니다!
Theorem.
IF $z_0$ is a pole of $f(z)$, THEN
proof.
증명은 아주 간단하다.
이때, $\left\{ \sum^{\infty}_{n=0} {a_n (z-z_0)^{n+m}} + \left( b_1 (z-z_0)^{m-1} + b_2 (z-z_0)^{m-2} + \cdots + b_m \right) \right\}$는 power series이므로 analytic 하다.
$f(z)$에 대해 $z \rightarrow z_0$로 극한을 취하면,
\[\underset{z \rightarrow z_0}{\lim} {\lvert f(z) \rvert} = \infty \cdot b_m = \infty\]가 된다.
essential singular point
Example.
What is $\underset{z \rightarrow 0}{\lim} e^{1/z}$ ?
Sol.
$e^z$에서 $1/z$를 대입해주면 쉽게 로랑 급수를 얻을 수 있다.
이제 $\underset{z \rightarrow 0}{\lim} e^{1/z}$를 구해보자. 과정이 조금 tricky 하다.
Let $z=x+iy$, THEN $\exp z = e^x \cdot e^{iy}$
이때, $e^{iy}$는 $2{\pi}$-periodic이다.
$e^{1/z}$에서 $0 < \lvert z \rvert < r$ ($r$ is small)의 Image를 생각해보자.
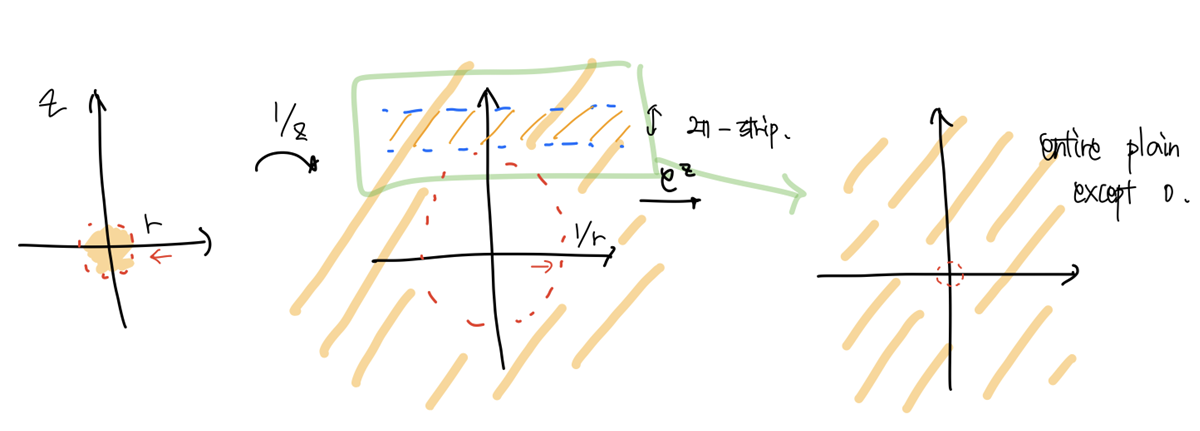
그러면, $r$을 아무리 작게 잡아도 $2{\pi}$-strip을 포함하게 되고, 따라서 $e^{1/z}$는 0을 제외한 복소 평면 전체가 된다!!
따라서 $\underset{z \rightarrow 0}{\lim} e^{1/z}$은 $0$을 제외한 복소 평면의 어느 값이든 될 수 있다!
Theorem. (Great) Picard’s Theorem
IF $f(z)$ is analytic except at $z_0$, and $z_0$ is an isolated essential singular point, THEN in any $\epsilon$-neighborhood of $z_0$, $f(z)$ takes every value, with at most one exceptional value.
// 증명 없이 소개만 하고 넘어갔다!
zeros and poles
Consider
\[f(z) = \frac{g(z)}{h(z)}\]where $g(z)$ and $h(z)$ are analytic.
THEN, the singular points of $f(z)$ are zeros of $h(z)$.
(아주 당연한 진술이다!)
Definition.
Let $f$ be analytic at $z_0$. IF $f(z_0)=0$ and there is a positive integer $m$ such that
THEN $f$ is said to have a zero of order $m$ at $z_0$.
IF $m=1$, THEN it is called a simple zero.
즉, $f(z_0)=0$이고, $f’(z_0) \ne 0$인 경우를 말한다.
Example. Talyor series
Taylor series where $f(z)$ is a zero of order $m$ at $z_0$.
테일러 급수에서 계수 $a_k$에 대해 살펴보자.
\[a_k = \frac{f^{(k)}(z_0)}{k!}\]이때, $f(z)$가 $z_0$에서 order $m$이므로 $k = 0, 1, \cdots, m-1$에서 $a_k=0$이다.
따라서 $f(z)$는
\[\begin{aligned} f(z) &= \left( a_0 + a_1 (z-z_0) + a_2 (z-z_0)^2 + \cdots + a_{m-1} (z-z_0)^{m-1} \right) + a_m (z-z_0)^m + \cdots \\ &= 0 + a_m (z-z_0)^m + \cdots \end{aligned}\]이때, 남은 텀들에서 $(z-z_0)^m$를 묶을 수 있다.
\[f(z) = (z-z_0)^m \left( a_m + a_{m+1} (z-z_0)^{m+1} + \cdots \right)\]$g(z) = a_m + a_{m+1} (z-z_0)^{m+1} + \cdots$라고 하자. 그러면, $g(z_0) \ne 0$이 된다.
즉, $f(z)$가 정확히 $m$개 중근을 가진다.
정리하면, 함수 $f(z)$가 a zero of order $m$ at $z_0$이라면, 함수 $f(z)$는 $m$개 중근을 가진다.
Theorem.
IF $z_0$ is a zero of order $m$, THEN there is an analytic function $g(z)$ such that
Theorem.
Let $f(z)$ be analytic at $z=z_0$ and have a zero of $m$-th order at $z=z_0$. THEN $1/f(z)$ has a pole of $m$-th order at $z=z_0$. And so does $g(z)/f(z)$ provided $g(z)$ is analytic at $z=z_0$ and $g(z_0) \ne 0$.
proof.
By previous theorem, $f(z)=(z-z_0)^{m}g(z)$ where $g(z)$ is analytic, and $g(z_0) \ne 0$.
Therefore,
\[\frac{1}{f(z)} = \frac{1}{(z-z_0)^m} \cdot \frac{1}{g(z)}\]이때, $\frac{1}{g(z)}$가 $z_0$에서 analytic이므로 Talyor series로 표현 가능하다.
\[\begin{aligned} \frac{1}{f(z)} &= \frac{1}{(z-z_0)^m} \cdot \frac{1}{g(z)} \\ &= \frac{1}{(z-z_0)^m} \cdot \left(a_0 + a_1 (z-z_0) + \cdots \right) \\ &= \frac{a_0}{(z-z_0)^m} + \frac{a_1}{(z-z_0)^{m-1}} + \cdots \end{aligned}\]따라서 $1/f(z)$는 order $m$의 pole을 가진다. $\blacksquare$
Example. $\cot z$
이때, $\sin z$가 $z=0, \pm \pi, \pm 2\pi, \cdots$ 에서 0이 되며, 모두 simple zero 이다.
Therefore, $\cot z$ has pole at $0, \pm \pi, \pm 2\pi, \cdots$ of order $1$.
Example.
Find poles of $f(z)$
Sol.
함수의 zeros와 pole에 대한 정리에 의해 $f(z)$의 pole은 $z^4+4 = 0$이 되는 지점이 된다.
\[\begin{aligned} z^4+4 &= 0 \\ z^4 &= -4 \\ (re^{i\theta})^4 &= 4 e^{i(\pi + 2n\pi)} \\ r^4 \cdot e^{i(4\theta)} &= 4 \cdot e^{i(\pi + 2n\pi)} \end{aligned}\] \[r = \sqrt{2}, \quad \theta = \frac{\pi}{4} + \frac{1}{2}k\pi, \quad (k=0, 1, 2, 3) \\\] \[z = 1 + i, \; 1-i, \; -1+i, \; -1-i\]