Applications to real integrals

2020-2학기, 대학에서 ‘응용복소함수론’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

---

복소 적분의 결과를 이용해 실수 영역에서의 적분을 해결할 수 있습니다 ㅎㅎ

residue를 이용해 두 가지 형태의 적분을 쉽게 다룰 수 있습니다.

1. Integrals of rational functions of $\cos \theta$ and $\sin \theta$

\[\int^{2{\pi}}_{0} {F(\cos \theta, \sin \theta) d\theta}\]

2. Improper integrals

\[\int^{\infty}_{0} {f(x) \; dx} \quad \textrm{or} \quad \int^{\infty}_{-\infty} {f(x) \; dx}\]

---

Integrals of rational functions of $\cos \theta$ and $\sin \theta$

\[\int^{2{\pi}}_{0} {F(\cos \theta, \sin \theta) d\theta}\]

Main idea.
Use $z=e^{i\theta}$

예제를 먼저 살펴보자!

Example.

\[\int^{2{\pi}}_{0} {\frac{1}{\sqrt{2} - \cos\theta} d\theta}\]

Sol.
치환 적분의 아이디어를 사용한다!

\[\cos \theta = \frac{e^{i\theta} + e^{-i\theta}}{2} = \frac{1}{2} \left( z + \frac{1}{z} \right)\] \[\begin{aligned} z &= e^{i\theta} \\ dz &= i \cdot e^{i\theta} d\theta \\ &= i \cdot z \; d\theta \end{aligned}\]

$dz = i \cdot z \; d\theta$를 잘 정리하면,

\[\begin{aligned} dz &= i \cdot z \; d\theta \\ \frac{1}{iz} \; dz &= d\theta \end{aligned}\]

이제 적분 범위에 대해 살펴보자.

$\theta: 0 \rightarrow 2\pi$ 이므로 $z$로의 치환을 잘 살펴보면, 주어진 적분은 $\lvert z \rvert = 1$에 대한 contour 적분을 하는 것과 동일하다!

따라서

\[\begin{aligned} \int^{2{\pi}}_{0} {\frac{1}{\sqrt{2} - \cos\theta} d\theta} &= \oint_{C} \frac{1}{\sqrt{2} - \frac{1}{2}\left(z+\frac{1}{z}\right)} \frac{dz}{iz} \\ &= \frac{1}{i} \cdot \oint_{C} \frac{1}{\sqrt{2} z - \frac{z^2+1}{2}} dz \\ &= - \frac{1}{2i} \oint_{C} \frac{1}{z^2 - 2\sqrt{2}z + 1} dz \end{aligned}\]

Let $q(z) = z^2 - 2\sqrt{2}z + 1$, THEN

\[\begin{aligned} q(z) = z^2 - 2\sqrt{2}z + 1 &= 0\\ z^2 - 2\sqrt{2}z + 2 &= 1 \\ z^2 - 2\sqrt{2}z + (\sqrt{2})^2 &= 1 \\ (z-\sqrt{2})^2 &= 1 \\ \therefore \quad z &= \pm 1 + \sqrt{2} \end{aligned}\]

이제 $f(z)$의 pole과 contour 사이 포함 관계를 잘 파악하여 적분을 잘 수행한다.

$z=\sqrt{2} - 1 < 1$ 이므로 $z=\sqrt{2} - 1$는 contour $\lvert z \rvert < 1$ 내부에 존재한다.

따라서 $f(z)$에 대한 적분은 $z=\sqrt{2} - 1$에 대한 residue를 구하는 것으로 쉽게 구할 수 있다!

\[\underset{z=\sqrt{2} - 1}{\textrm{Res}} f(z) = \lim_{z \rightarrow \sqrt{2} - 1} \frac{1}{z-(\sqrt{z} + 1)} = - \frac{1}{2}\]

따라서

\[\begin{aligned} \int^{2{\pi}}_{0} {\frac{1}{\sqrt{2} - \cos\theta} d\theta} &= \oint_{C} \frac{1}{\sqrt{2} - \frac{1}{2}\left(z+\frac{1}{z}\right)} \frac{dz}{iz} \\ &= - \frac{1}{2i} \oint_{C} \frac{1}{z^2 - 2\sqrt{2}z + 1} dz \\ &= - \frac{1}{2i} \cdot \left\{ 2{\pi}i \cdot \underset{z=\sqrt{2} - 1}{\textrm{Res}} f(z) \right\} \\ &= - \frac{1}{2i} \cdot \left\{ 2{\pi}i \cdot - \frac{1}{2} \right\} \\ &= \frac{\pi}{2} \end{aligned}\]

$\blacksquare$

---

Example.
Let $-1 < a < 1$,

\[\int^{2\pi}_{0} \frac{1}{1+a\sin\theta} d\theta = \frac{2\pi}{\sqrt{1-a^2}}\]

---

Improper integral

\[\int^{\infty}_{0} {f(x) \; dx} \quad \textrm{or} \quad \int^{\infty}_{-\infty} {f(x) \; dx}\]

Improper integral은 적분 범위에 $\infty$가 있는 것이 특징이다.

이것 역시 예제를 통해 residue를 어떻게 쓰는지 살펴보자.

---

Example.

\[\int^{\infty}_{-\infty} \frac{1}{1+x^2} dx\]

Sol.

먼저, improper integral을 극한과 함께 다시 써보자.

\[\int^{\infty}_{-\infty} \frac{1}{1+x^2} dx = \lim_{R \rightarrow \infty} \int^{R}_{-R} \frac{1}{1+x^2} dx\]

Let $f(z) = \frac{1}{1+x^2}$, THEN there are two poles at $z=i$ and $z=-i$.

이제 적분할 contour를 다음과 같이 잡아보자.

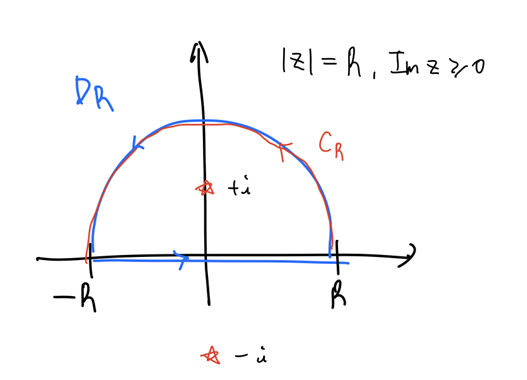
그리고 contour 적분을 해보면,

\[\oint_{D_R} f(z) dz = \int^{R}_{-R} f(z) dz + \int_{C_R} f(z) dz\]

여기서 $\oint_{D_R} f(z) dz$는 residue thm에 따라

\[\begin{aligned} \oint_{D_R} f(z) dz &= \oint_{D_R} \frac{1}{1+z^2} dz \\ &= \oint_{D_R} \frac{1}{(z+i)(z-i)} \\ &= 2{\pi}i \cdot \underset{z=i}{\textrm{Res}} \frac{1}{(z+i)(z-i)} \\ &= 2{\pi}i \cdot \frac{1}{2i} = \pi \end{aligned}\]

이제 적분에서 arc integral인 $\int_{C_R} f(z) dz$에 대해 살펴보자.

이때, $\int_{C_R} f(z) dz$의 정확한 적분값은 구하지 않고, ML-inequality를 사용해 bound만 구할 것이다.

\[\begin{aligned} \left\lvert \int_{C_R} \frac{1}{1+z^2} dz \right\rvert &\le \frac{1}{R^2 - 1} \cdot {\pi}R \\ & \rightarrow 0 \quad \textrm{as} \quad R \rightarrow \infty \end{aligned}\]

즉, $R \rightarrow \infty$ 일 때, $\int_{C_R} f(z) dz$가 0으로 수렴하므로

\[\begin{aligned} \lim_{R \rightarrow \infty} \left\{ \oint_{D_R} f(z) dz \right\} &= \lim_{R \rightarrow \infty} \left\{ \int^{R}_{-R} f(z) dz \right\} + \lim_{R \rightarrow \infty} \left\{ \int_{C_R} f(z) dz \right\} \\ \pi &= \lim_{R \rightarrow \infty} \left\{ \int^{R}_{-R} f(z) dz \right\} + 0\\ \pi &= \int^{\infty}_{-\infty} f(z) dz \end{aligned}\]

Therefore,

\[\int^{\infty}_{-\infty} \frac{1}{1+z^2} dz = \pi\]

$\blacksquare$

---

Definition. improper integral
IF $f(z)$ is continuous on $(-\infty, \infty)$

\[\int^{\infty}_{\infty} f(x) \; dx = \lim_{R_1 \rightarrow \infty} \int^{a}_{-R_1} f(x) \; dx + \lim_{R_2 \rightarrow \infty} \int^{R_2}_{a} f(x) \; dx\]

Definition. Cauchy principal value of improper integral

만약 improper integral에 대한 두 적분의 극한값이 존재한다면,

Cauchy principal value of $\int^{\infty}_{\infty} f(x) \; dx$ is defined by

\[\lim_{R \rightarrow \infty} \int^{R}_{-R} f(x) \; dx\]

Caution!
일반적으로 improper integral과 Cauchy P.V.를 같다고 단정할 순 없음!

Example.
Calculate both improper integral and Cauchy P.V.

\[\int^{\infty}_{-\infty} x \; dx\]

1. impropr integral

\[\begin{aligned} \int^{\infty}_{-\infty} x \; dx &= \lim_{R_1 \rightarrow \infty} \int^{0}_{-R_1} x \; dx + \lim_{R_2 \rightarrow \infty} \int^{R_2}_{0} x \; dx \\ &= -\infty + \infty \\ &= \textrm{undefined} \end{aligned}\]

2. Cauchy P.V.

\[\begin{aligned} \int^{\infty}_{-\infty} x \; dx &= \lim_{R \rightarrow \infty} \int^{R}_{-R} x \; dx \\ &= 0 \quad (\because x \textrm{ is odd function.}) \end{aligned} \\\]

따라서 일반적으로 improper integral과 Cauchy P.V.를 같다고 단정할 순 없다! $\blacksquare$