Linear Transform

2020-2학기, 대학에서 ‘응용복소함수론’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

---

Linear Transformation

\[w = Az + B \quad (A \ne 0)\]

위와 같은 형태의 변환은 Linear Transform이라고 한다.

복소 영역에서 Linear Transform이 어떻게 행동하는지 케이스 별로 살펴보자.

(1) $B=0$

\[w = Az \quad (A \ne 0)\]

$A = a \cdot e^{i\alpha}$, $z = r \cdot e^{i\theta}$라고 두면, $w$는 $w = (ar) \cdot e^{i(\theta + \alpha)}$가 된다.

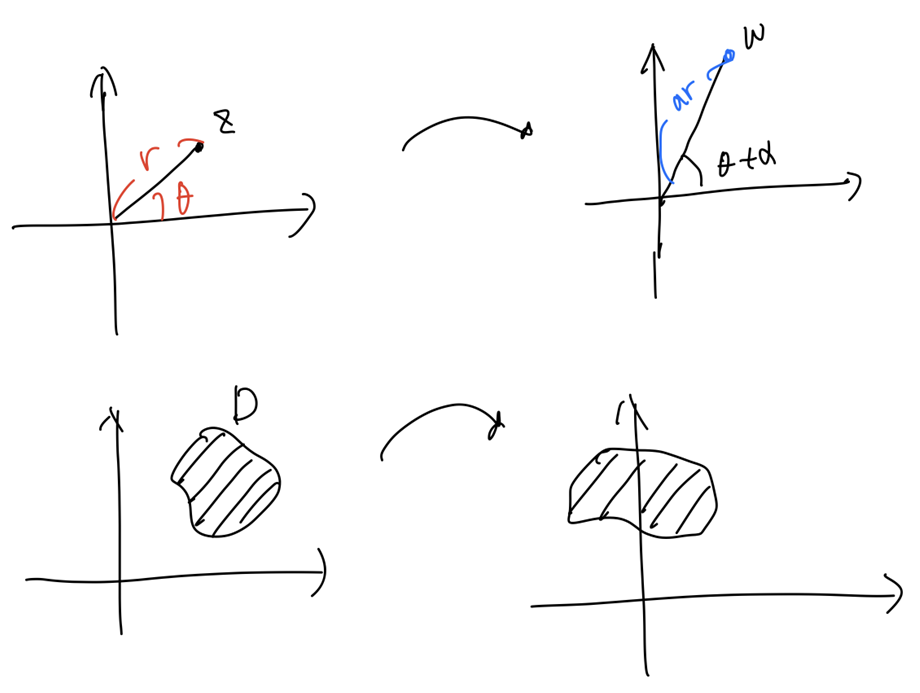
• 각도 $\alpha$ 만큼 Domain이 회전 이동
• $a = \lvert A \rvert$ 만큼 수축/팽창

(2) $A=1$

\[w = z + B\]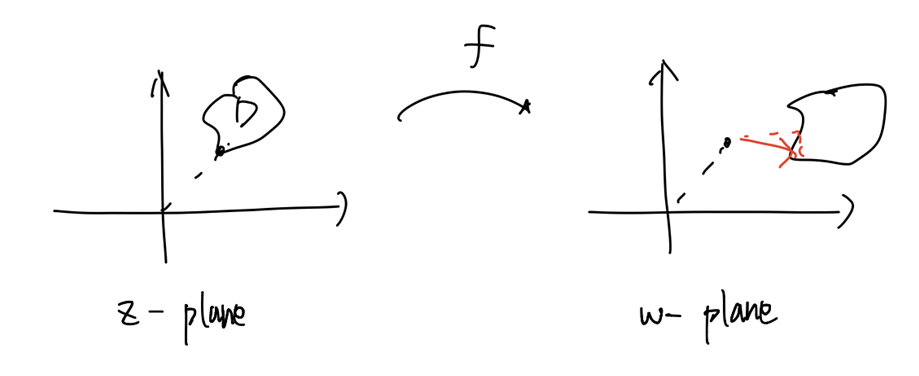

• $B$ 만큼 평행 이동

(3) General form

\[w = Az + B\]

(1), (2)의 상황이 합성된 상황으로 이해할 수 있다.

\[z \longrightarrow Az \longrightarrow Az + B\]

---

Image of Linear transform; Square Domain

The image of the set $\{ x + ig : 0 \le x \le 1, \; 0 \le y \le 2 \}$ under the map

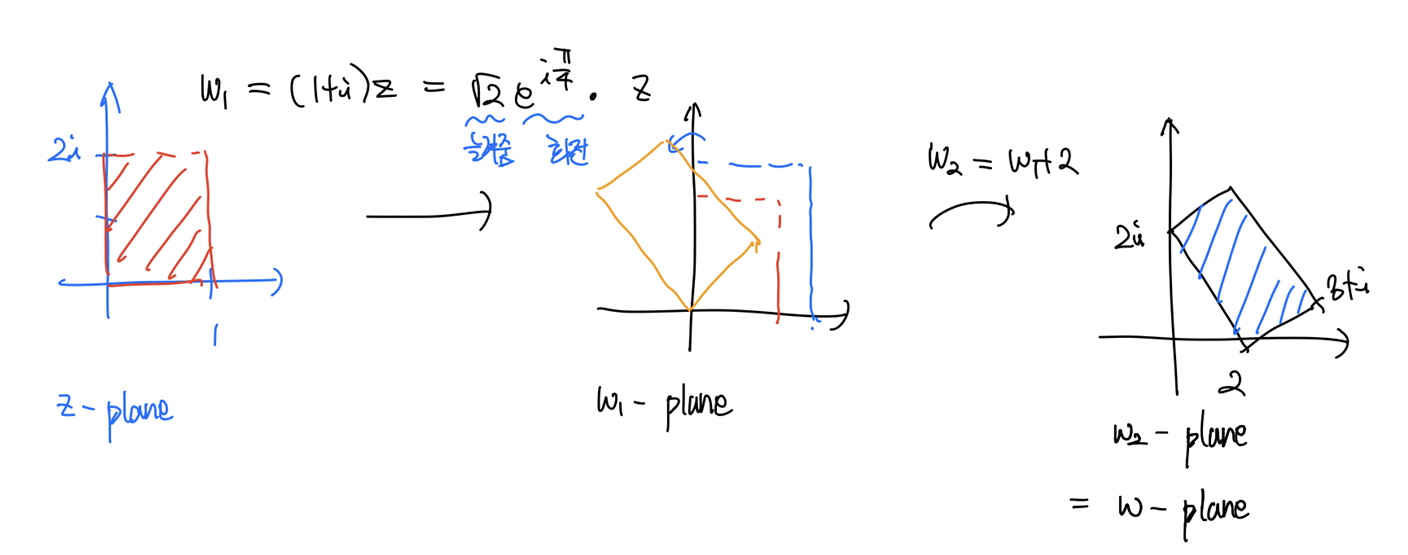
\[w = (1+i)z + 2\]

transform $w$를 두 단계로 나누어 실시하자.

1. $w_1 = (1+i)z$
2. $w_2 = w_1 + 2$

---

Inversion mapping; $w = \frac{1}{z}$

Write $z = r \cdot e^{i\theta}$, THEN $w = \frac{1}{r} \cdot e^{-i\theta}$

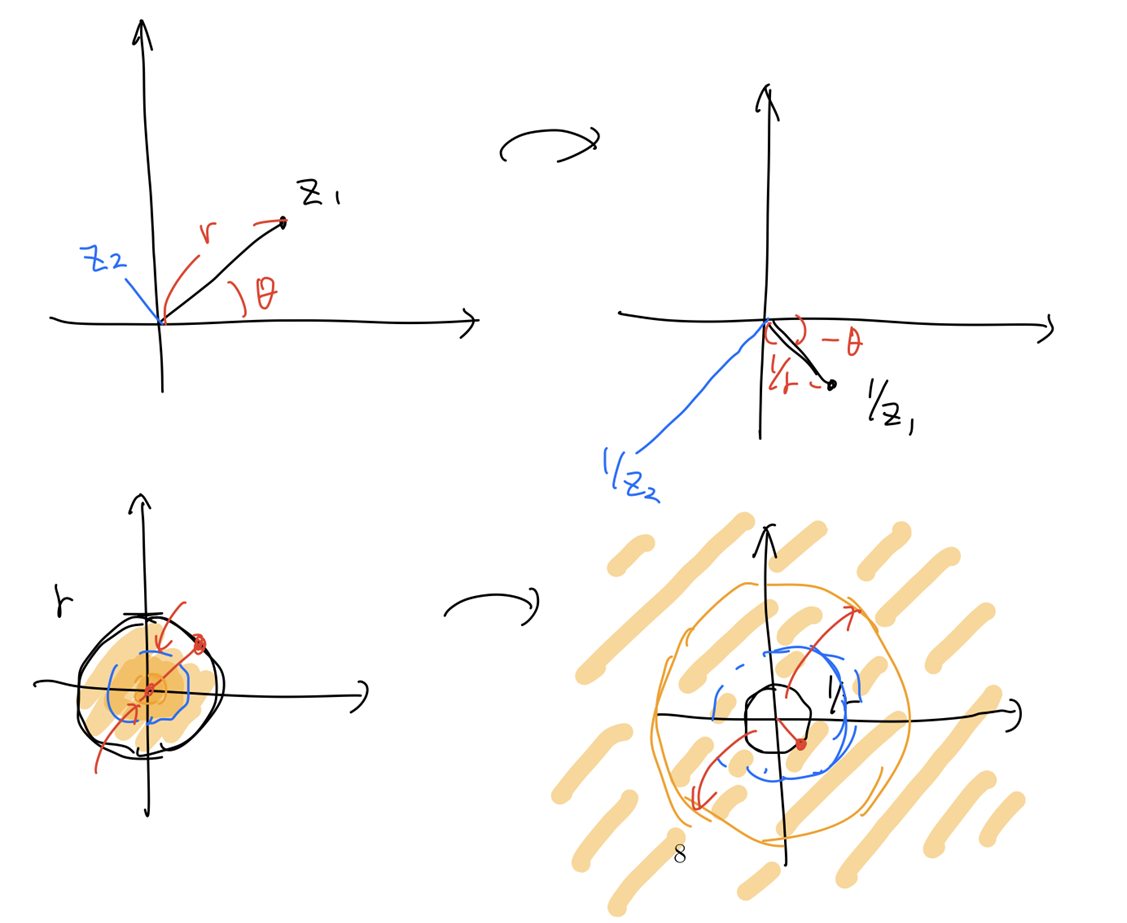
inversion mapping $w = \frac{1}{z}$는 $z$를 x-축으로 반전시키고, 길이를 수축/팽창시킨다.

$\frac{1}{r}$을 취하기 때문에 복소수 $z$가 원점 $O$에 가까워질 수록 image가 발산한다.

Extended complex plane; $\mathbb{C} \cup \{ \infty \}$

Transform $T(z)$를 nice하게 정의하기 위해서 $\{ \infty \}$를 추가해 이미지 영역을 확장시킨다.

For a transform $T(z) = \frac{1}{z}$, Let $T(0) = \infty$ and $T(\infty) = 0$, THEN $T$ is continuous.

Picture from link

¹

원래 $T(z)$는 $0$에서 값이 정의되지 않는다. 그런데 Extended complex plane을 생각해서 $T(0) = \infty$로 값을 부여하는 것이다. 즉, $\infty$라는 한 점을 추가해 Image space를 $\mathbb{C}$에서 $\mathbb{C} \cup \{ \infty \}$로 확장한다면, $T(z)$를 $z=0$에서까지 continuous하게 만들 수 있다.

\[\lim_{z \rightarrow 0} {T(z)} = \infty = T(0)\]

이를 통해 $T(z)$를 복소평면 전체에서 continuous하게 정의할 수 있다.

---

Images of inversion mapping

(1) $x=c$ under $w = \frac{1}{z}$

\[\begin{aligned} w &= u + i v = \frac{1}{x + iy} \\ z &= x + iy = \frac{1}{u + iy} = \frac{u}{u^2 + v^2} - i \frac{v}{u^2 + v^2} \end{aligned}\] \[\begin{aligned} x = \frac{u}{u^2 + v^2} &= c \\ c(u^2 + v^2) - u &= 0 \\ u^2 + v^2 - \frac{1}{c} u &= 0 \\ \left(u - \frac{1}{2c}\right)^2 + v^2 &= \left( \frac{1}{2c} \right)^2 \end{aligned}\]

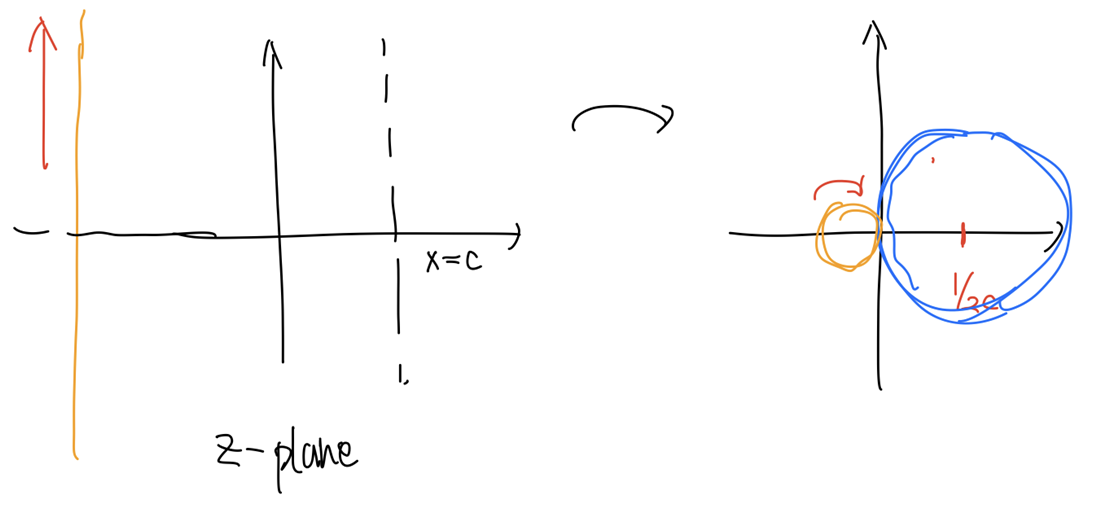
따라서 직선 $x=c$는 w-plane에 원으로 매핑된다.

(2) $\{ x + iy : x \ge c \}$ under $w = \frac{1}{z}$

---

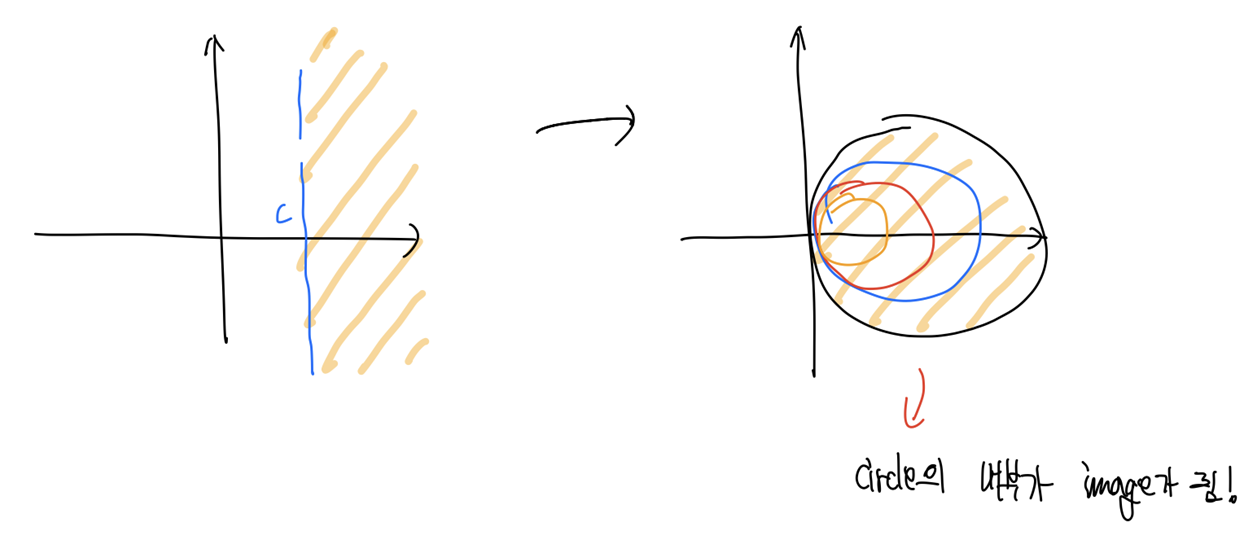
Statement.

$w=\frac{1}{z}$ transforms (circles and lines) into (circles and lines).

일반적으로 circle과 line은 아래의 식으로 표현된다.

\[A(x^2 + y^2) + Bx + Cy + D = 0 \quad (B^2 + C^2 > 4 AD)\]

* line
$A=0$: $Bx + Cy + D = 0$

* circle
$A \ne 0$: $\left(x + \frac{B}{2A}\right)^2 + \left( y + \frac{C}{2A}\right)^2 = \left(\frac{\sqrt{B^2 + C^2 - 4 AD}}{2A}\right)^2$

이때, 우리가 $(x, y)$와 $(u, v)$에 대한 관계식을 알고 있으니, $(x, y)$에 대한 위의 식을 $(u, v)$에 대한 식으로 바꿀 수 있다!

\[\begin{aligned} w &= u + iv \\ z &= x + iy = \frac{1}{u + iv} = \frac{u}{u^2 + v^2} - i \frac{v}{u^2 + v^2} \end{aligned}\]

위의 관계식으로부터

(1) $x = \dfrac{u}{u^2 + v^2}$, $y = -\dfrac{v}{u^2 + v^2}$

(2) $x^2 + y^2 = \dfrac{1}{u^2 + v^2}$

를 유도할 수 있고,

\[\begin{aligned} A(x^2 + y^2) + Bx + Cy + D &= 0 \quad (B^2 + C^2 > 4 AD) \\ A\left(\frac{1}{u^2 + v^2}\right) + B\left(\frac{u}{u^2 + v^2}\right) + C\left(-\frac{v}{u^2 + v^2}\right) + D &= 0 \\ D(u^2 + v^2) + Bu + C(-v) + A &= 0 \end{aligned}\]

따라서 inversion mapping $w = \frac{1}{z}$에 대한 Image는 line 또는 circle이 된다.

$A$, $D$에 따른 경우를 표로 분류하면 아래와 같다.

---

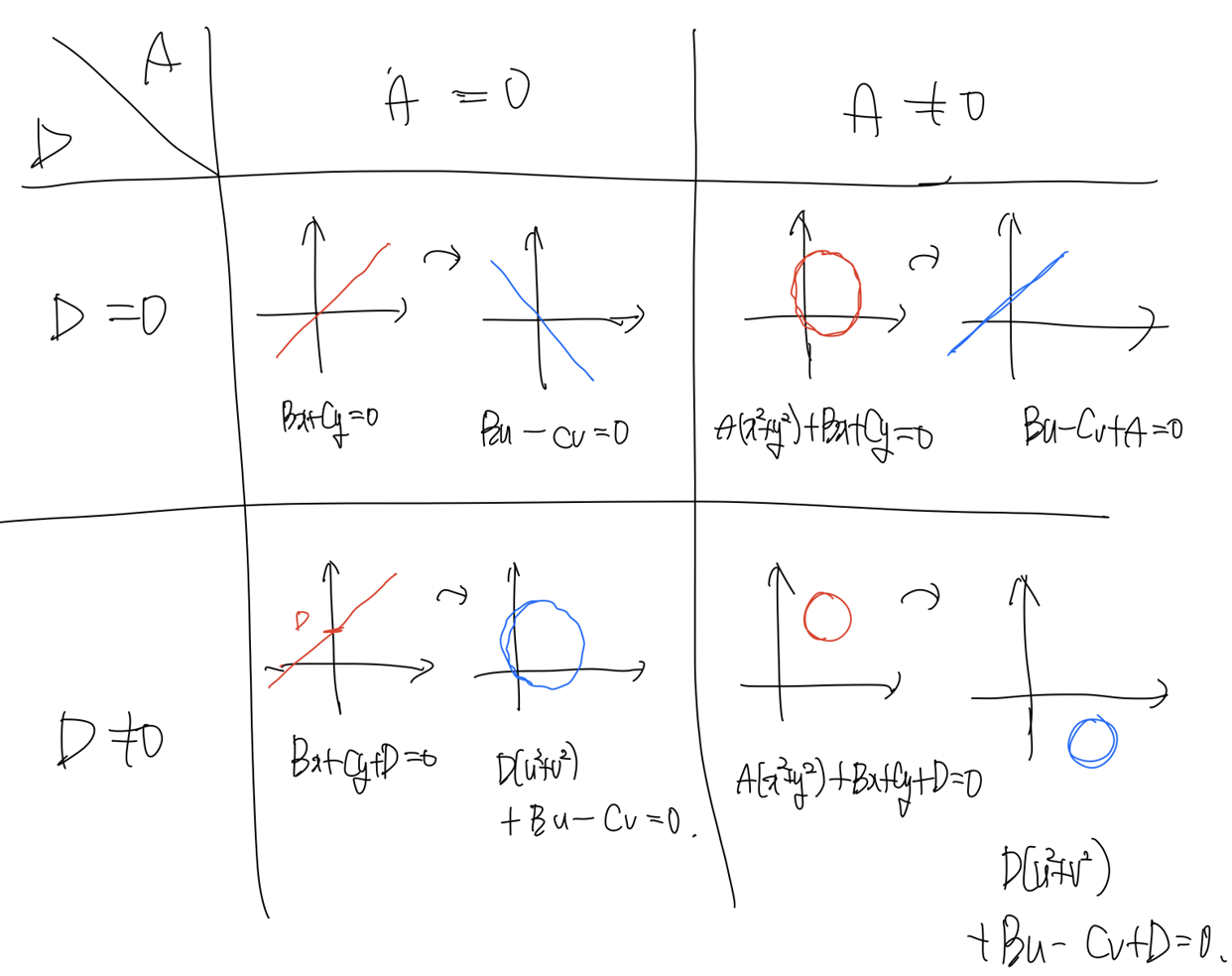
1. 참고로 이런 Extended Complex Plane을 “Riemann Sphere”라고도 한다. 이 Sphere를 사용하면, 복소평면 상의 모든 점을 구의 표면을 매핑시킬 수 있다! ↩