Sequential Density Estimation
본 글은 2020-2학기 “컴퓨터 비전” 수업을 듣고, 스스로 학습하면서 개인적인 용도로 정리한 것입니다. 지적은 언제나 환영입니다 :)
Bayes Theorem
\[P(H \mid E) = \frac{P(E \mid H) P(H)}{P(E)}\]베이즈 정리는 사전 확률과 사후 확률 사이 관계에 대한 정리이다. 베이즈 정리 또는 베이즈 이론의 핵심은 사건 $E$가 발생했을 때, 확률 $P(H)$를 갱신하는 것이다. 다르게 표현하자면, 데이터 $X$가 관찰 되었을 때, 분포 $P(x)$를 갱신하는 것이다.
용어 정리
- $P(H)$: Prior probability
- 현재 가지고 있는 정보를 기반으로 정한 확률 (또는 분포)
- $P(H \mid E)$: Posteriori probability
- 사건 발생 후, 갱신된 확률 (또는 분포)
- 사전 정보 또는 데이터를 추가함으로써 수정된 확률이다.
- $P(E \mid H)$: likelihood
- 관측된 사건 $E$가 발생할 확률
Markov Assumption
<마르코프 가정; Markov Assumption>은 복잡한 확률의 과정을 단순하게 만들어 준다.
So, $x_{t+1}$ is independent to other past states $x_{1:t-1}$
Density Estimation
밀도 추정; Density Estimation은 관측된 데이터들의 분포 $z_{1:t}$를 바탕으로 변수 $x_t$의 확률 분포의 특성을 추정하는 작업이다. $p(x_t \mid z_{1:t})$
이때 변수 $x_t$의 밀도(density)를 추정하는 것은 곧, $x_t$의 확률밀도함수(pdf; probability density function)을 추정하는 것이다.
Hidden Markov Model
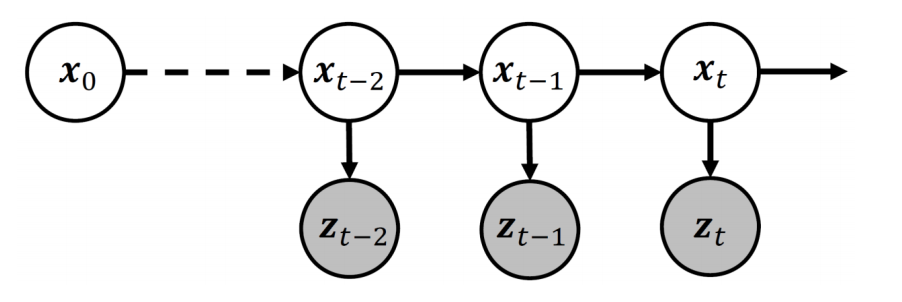
은닉 마르코프 모델; Hidden Markov Model은 Sequential data를 다루는데 사용하는 모델이다.
HMM은 마르코프 가정을 따른다. 따라서
\[\begin{aligned} p(x_t \mid x_{1:t-1}) &= p(x_t \mid x_{t_1})\\ p(z_t \mid x_{1:t}) &= p(z_t \mid x_t) \end{aligned}\]의 성질을 만족한다.
위의 두 성질은 Sequential data에서 Density Estimation 하는 데에 중요한 도구로 사용된다!
Sequential Density Estimation
Sequential Density Estimation은 Sequential data에 대한 pdf를 추정하는 과정이다.
즉, pdf $p(x_t \mid z_{1:t})$를 추정한다.
과정이 좀 복잡한데, 천천히 살펴보자.
먼저 조건부 확률인 $p(x_t \mid z_{1:t})$를 베이즈 정리를 이용해 분리한다.
\[\begin{aligned} p(x_t \mid z_{1:t}) = \frac{p(x_t, z_{1:t})}{p(z_{1:t})} \end{aligned}\]이때, 분모의 $p(z_{1:t})$는 observation에 대한 확률이며, 상수라고 가정한다.
따라서, $p(x_t \mid z_{1:t})$는 아래와 같다.
\[\begin{aligned} p(x_t \mid z_{1:t}) \propto p(x_t, z_{1:t}) \end{aligned}\]이제 우리의 목표는 $p(x_t \mid z_{1:t})$를 구하는 것에서 $p(x_t, z_{1:t})$를 구하는 것이 되었다.
\[\begin{aligned} p(x_t, z_{1:t}) = \int \cdots \int \int p(x_{1:t}, z_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \end{aligned}\]위의 식은 $p(x_t, z_{1:t})$를 구하는 방법에 대한 기술이다. 식을 좌에서 우로 이해하는 것보다는 우에서 좌로 이해해야 한다.
\[\begin{aligned} \int \cdots \int \int p(x_{1:t}, z_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \end{aligned}\]를 가장 안쪽에 있는 적분식부터 이해해보자.
\[\begin{aligned} \int p(\{ x_1, \cdots, x_{t_1}, x_t \}, z_{1:t}) \; dx_1 \end{aligned}\]이것은 $p(\{ x_1, \cdots, x_{t_1}, x_t \}, z_{1:t})$에서 $x_1$를 추출하는(marginalize out) 과정이다.
이때, $x_1$는 $\{ x_2, \cdots, x_{t_1}, x_t \}$와 $\{ z_1, \cdots, z_t \}$에 모두 indenpendent하므로
- $x_1 \perp x_i \quad (2 \le i \le t)$
- $x_1 \perp z_j \quad (1 \le j \le t)$
가 된다.
이 과정을 $x_2$부터 $x_{t-1}$까지 반복하면, 아래와 같은 결과를 얻을 수 있다.
\[\begin{aligned} p(x_t, z_{1:t}) = \int \cdots \int \int p(x_{1:t}, z_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \end{aligned}\]이번에는 중첩된 적분식에서 적분되는 함수인 $p(x_{1:t}, z_{1:t})$를 살펴보자.
$p(x_{1:t}, z_{1:t})$는 베이즈 정리에 의해 아래와 같이 표현된다.
\[\begin{aligned} p(x_{1:t}, z_{1:t}) = p(z_{1:t} \mid x_{1:t}) \cdot p(x_{1:t}) \end{aligned}\]따라서 중첩된 적분식을 다시 쓰면,
\[\begin{aligned} & \int \cdots \int \int p(x_{1:t}, z_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \\ =& \int \cdots \int \int p(z_{1:t} \mid x_{1:t}) \cdot p(x_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \end{aligned}\]가 된다.
이제 함수 $p(z_{1:t} \mid x_{1:t}) \cdot p(x_{1:t})$를 주목해보자.
먼저 위의 식에서 $p(x_{1:t})$ 부분은 probabilistic dependency에 의해 아래와 같이 표현할 수 있다.
\[p(x_{1:t}) = p(x_t \mid x_{t-1}) \cdots p(x_2 \mid x_1) p(x_1)\]$p(z_{1:t} \mid x_{1:t})$ 부분 역시 probabilistic dependency에 의해 아래와 같이 표현된다.
\[p(z_{1:t} \mid x_{1:t}) = p(z_t \mid x_t) \cdots p(z_2 \mid x_2) p(z_1 \mid x_1)\]종합하면, 아래와 같다.
\[\begin{aligned} p(z_{1:t} \mid x_{1:t}) & \cdot p(x_{1:t}) \\ = \left( p(x_t \mid x_{t-1}) \cdots p(x_2 \mid x_1) p(x_1) \right) & \cdot \left( p(z_t \mid x_t) \cdots p(z_2 \mid x_2) p(z_1 \mid x_1) \right) \end{aligned}\]이것을 적분식에 반영하면 아래와 같다.
\[\begin{aligned} & \int \cdots \int \int p(z_{1:t} \mid x_{1:t}) \cdot p(x_{1:t}) \; dx_1 dx_2 \cdots dx_{t-1} \\ = & \int \cdots \int \int p(z_{1:t} \mid x_{1:t}) \cdot \left( p(x_t \mid x_{t-1}) \cdots p(x_2 \mid x_1) p(x_1) \right) \cdot \left( p(z_t \mid x_t) \cdots p(z_2 \mid x_2) p(z_1 \mid x_1) \right) \cdots dx_{t-1} \end{aligned}\]식이 아주아주 복잡해졌다 ㅠㅠ
하지만, 위의 중첩된 적분식은 의외로 좋은 성질을 가지고 있다!!
위의 적분식에서 적분에 관여하지 않는 변수를 모두 분리해보자. 그러면 아래와 같은 식을 얻는다.
\[\begin{aligned} & \int \cdots \int \int p(z_{1:t} \mid x_{1:t}) \cdot \left( p(x_t \mid x_{t-1}) \cdots p(x_2 \mid x_1) p(x_1) \right) \cdot \left( p(z_t \mid x_t) \cdots p(z_2 \mid x_2) p(z_1 \mid x_1) \right) \cdots dx_{t-1} \\ =& \; p(z_{1:t} \mid x_{1:t}) \left( \int_{x_{t-1}} p(x_t \mid x_{t-1}) p(z_{t-1} \mid x_{t-1}) \cdots \left( \int_{x_2} p(x_3 \mid x_2)p(z_2 \mid x_2) \left( \int_{x_1} p(x_2 \mid x_1)p(z_1 \mid x_1) p(x_1) dx_1 \right) dx_2 \right) \cdots dx_{t-1} \right) \end{aligned}\]식이 더 길어졌다 ㅠㅠ
중접된 적분을 풀기 위해 가장 안쪽에서부터 시작해보자.
\[\int_{x_1} p(x_2 \mid x_1) p(z_1 \mid x_1) p(x_1) \; dx_1\]베이즈 정리에 의해 $p(z_1 \mid x_1) p(x_1) = \dfrac{p(z_1, x_1)}{p(x_1)} p(x_1) = p(z_1, x_1)$이다.
이때, $p(z_1, x_1) = \dfrac{p(x_1 \mid z_1)}{p(z_1)}$인데, $p(z_1)$이 상수이므로 $p(z_1, x_1) \propto p(x_1 \mid z_1)$이다.
정리하면,
\[p(z_1 \mid x_1) p(x_1) = p(z_1, x_1) \propto p(x_1 \mid z_1)\]따라서
\[\begin{aligned} & \int_{x_1} p(x_2 \mid x_1) p(z_1 \mid x_1) p(x_1) \; dx_1 \\ \propto& \int_{x_1} p(x_2 \mid x_1) p(x_1 \mid z_1) \; dx_1 \end{aligned}\]이때, $p(x_2 \mid x_1) p(x_1 \mid z_1)$를 잘 정리하여 $p(x_2, x_1 \mid z_1)$를 유도할 수 있다.
\[\begin{aligned} p(x_2, x_1 \mid z_1) &= \frac{p(x_2 \cap x_1 \cap z_1)}{p(z_1)} \\ &= \frac{p(x_2 \mid (x_1 \cap z_1)) \cdot p(x_1 \cap z_1)}{p(z_1)} \\ &= p(x_2 \mid x_1) \cdot \frac{p(x_1 \cap z_1)}{p(z_1)} \\ &= p(x_2 \mid x_1) \cdot p(x_1 \mid z_1) \end{aligned}\]따라서 적분식을 아래와 같이 바꿀 수 있다.
\[\begin{aligned} & \int_{x_1} p(x_2 \mid x_1) p(x_1 \mid z_1) \; dx_1 \\ =& \int_{x_1} p(x_2, x_1 \mid z_1) \; dx_1 \end{aligned}\]적분식을 계산하면, $x_1$이 marginalize out된다.
\[\begin{aligned} & \int_{x_1} p(x_2, x_1 \mid z_1) \; dx_1 \\ =& \, p(x_2 \mid z_1) \end{aligned}\]가장 안쪽 적분에서 얻은 결과를 활용해 그 다음 적분을 해결해보자.
\[\int_{x_2} p(x_3 \mid x_2) p(z_2 \mid x_2) p(x_2 \mid z_1) \; dx_2\]이번에는 $p(z_2 \mid x_2) \cdot p(x_2 \mid z_1)$를 변형한다.
\[\begin{aligned} & p(z_2 \mid x_2) \cdot p(x_2 \mid z_1) \\ =& \; p(z_2 \mid x_2) \cdot \frac{p(x_2 \cap z_1)}{p(z_1)} \\ =& \; \frac{p(z_2 \mid (x_2 \cap z_1)) \cdot p(x_2 \cap z_1)}{p(z_1)} \\ =& \; \frac{p(z_2 \cap x_2 \cap z_1)}{p(z_1)}\\ =& \; \frac{p(x_2 \cap (z_1 \cap z_2))}{p(z_1 \cap z_2)}\\ =& \; p(x_2 \mid z_1, z_2) \end{aligned}\]따라서 두번째 적분식은 아래와 같다.
\[\begin{aligned} & \int_{x_2} p(x_3 \mid x_2) p(z_2 \mid x_2) p(x_2 \mid z_1) \; dx_2 \\ =& \int_{x_2} p(x_3 \mid x_2) p(x_2 \mid z_1, z_2) \; dx_2 \\ =& \; p(x_3 \mid z_1, z_2) \end{aligned}\]위와 같은 방식으로 내부의 적분값을 이용해 적분을 계속 진행하면, 우리가 얻고자 하는 $p(x_t \mid z_{1:t})$를 얻을 수 있다.
$p(x_t \mid z_{1:t})$를 추정하는 Sequential Density Estimation은 내부에서 얻은 값을 활용해 다음 적분의 값을 구하는 과정으로 진행되기 때문에, 일종의 재귀(recursion)이라고 볼 수 있다.
