Cauchy’s Integral Formula
2020-2학기, 대학에서 ‘응용복소함수론’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Theorem. [Review] Goursat Theorem
Let $D$ be an open set in $\mathbb{C}$.
Let $T$ be a triangle such that $T$ and its interior lie in $D$.
If $f(z)$ is analytic in $D$, then
\[\oint_{T} f(z) dz = 0\]Theorem. Cauchy-Goursat Theorem for a disc
Let $f(z)$ be analytic in a disc $D$.
Then there is an analytic function $F(z)$ in $D$ such that
\[F'(z) = f(z) \quad \textrm{for} \; z \in D\]Corollary.
Let $f(z)$ be analytic in a disc $D$.
Then for any closed contour $C$ in $D$,
\[\oint_{C} f(z) \; dz = 0\]증명은 생각보다 간단하다.
논의의 편의를 위해 Disc $D$의 중심이 원점이라고 하자.
그리고 $F(z)$를 아래와 같이 정의하자.
\[F(z_0) = \int_{C} f(z) \; dz\]이제,
\[\lim_{h \rightarrow 0} \frac{F(z_0 + h) - F(z_0)}{h} = f(z_0)\]임을 보이자!
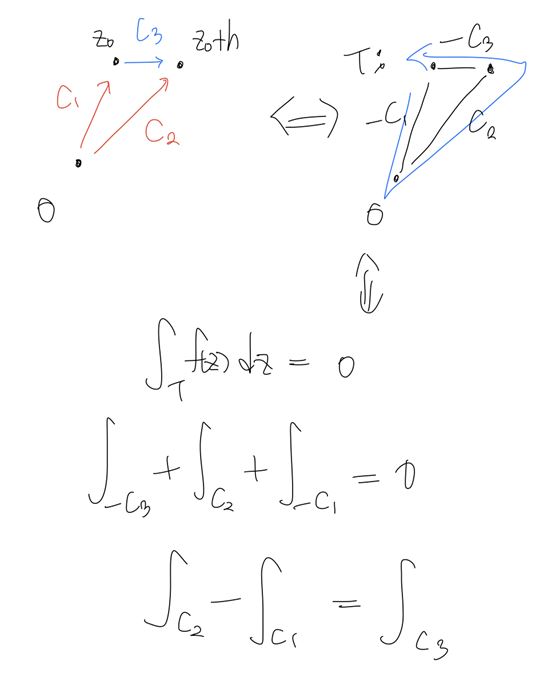
Then,
이때, $f(z_0)$에 대해 아래의 등식을 확인할 수 있다.
\[\begin{aligned} \frac{1}{h} \int_{C_3} f(z_0) \; dz &= f(z_0) \frac{1}{h} \int_{C_3} \; dz \\ &= f(z_0) \frac{1}{h} h \\ &= f(z_0) \end{aligned}\] \[\begin{aligned} &\frac{1}{h} \left( F(z_0 + h) - F(z_0) \right) - f(z_0) \\ &= \frac{1}{h} \int_{C_3} f(z) \; dz - \frac{1}{h} \int_{C_3} f(z_0) \; dz \\ &= \frac{1}{h} \int_{C_3} \left( f(z) - f(z_0) \right) \; dz \end{aligned}\]이제 위의 식에서 “ML-inequality“를 적용해보자!!
\[\begin{aligned} \left| \frac{1}{h} \int_{C_3} \left( f(z) - f(z_0) \right) \; dz \right| &= \frac{1}{\left| h \right|} \max_{z \in C_3} \left| f(z) - f(z_0) \right| \cdot \left| h \right| \\ &= \max_{z \in C_3} \left| f(z) - f(z_0) \right| \end{aligned}\]이때, $z \rightarrow z_0$ 할수록 $(z - z_0) \rightarrow 0$ 이므로 우변은 0이 된다.
즉,
\[\lim_{h \rightarrow 0} \frac{F(z_0 + h) - F(z_0)}{h} = f(z_0)\]이다!!
결론은 $F(z_0) = \int_{C} f(z) \; dz$로 둠으로써 $F’(z) = f(z)$가 되는 함수 $F(z)$를 찾았다!!
Generalization. Principles of Deformation of Contours
앞에서는 disc $D$에 대해 Cauchy Theorem을 적용했다면, 이번에는 일반적인 형태의 영역 $D$에서 Cauchy Theorem을 적용한다.
일반적인 simply connected domain $D$ 위에서 폐적분 closed integral이 0이 됨을 보이기 위해 아래의 식을 증명해야 한다.
\[\int_{C_1} f(z) \; dz = \int_{C_2} f(z) \; dz\]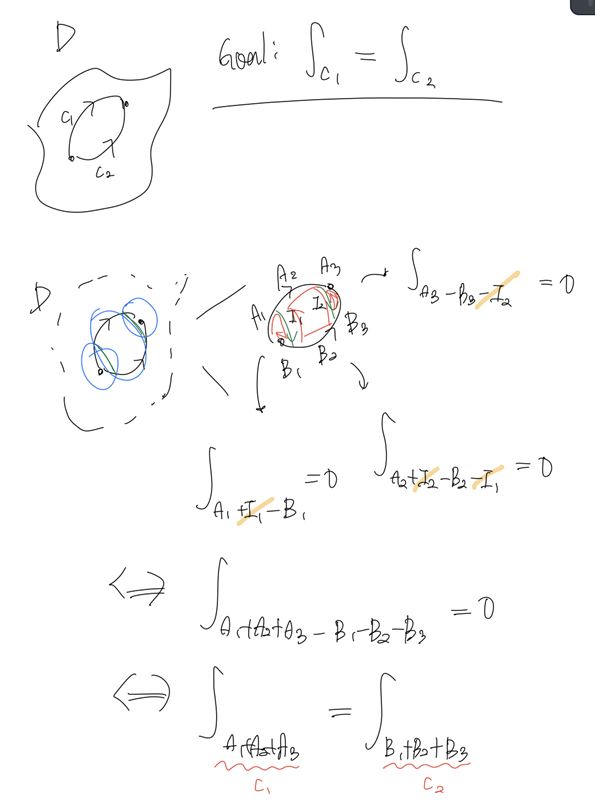
curve $C_1$, $C_2$를 가로지르는 3개의 disc를 생각해보자.
이미 앞에서 disc 내의 analytic function의 closed integral의 값은 0임을 확인했으므로, 3개의 disc로 적당히 나누어 curve $C_1$, $C_2$를 disc 내부의 closed curve 3개로 나눌 수 있다.
이제 disc 위에서 three closed integral을 잘 정리하면,
\[\int_{C_1} f(z) \; dz = \int_{C_2} f(z) \; dz\]의 결과를 얻을 수 있다.
Theorem.
Let $f(z)$ be analytic in a simply connected domain $D$,
then there is an analytic function $F(z)$ in $D$ s.t.
\[F'(z) = f(z) \quad \textrm{for} \; z \in D\]where $F(z)$ id defined as
\[F(z) = \int_{C} f(w) \; dw\]Multiply Connected Domains
지금까지는 Domain에 hole이 없는 “simply connected domain” 위에서 analytic function을 살펴보았다.
지금부터는 시야를 확장해서 Domain에 “hole”이 있는 경우를 살펴보자.
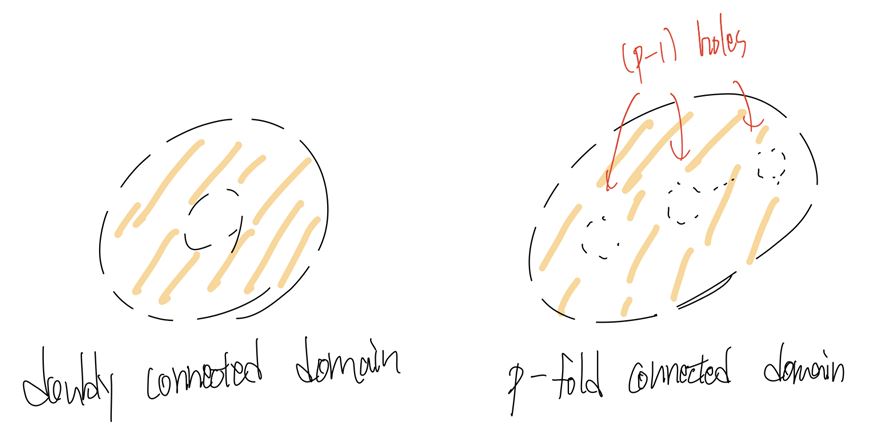
먼저 Domain에 hole이 하나 존재한다면, “doubly connected domain“이라고 한다. 만약 Domain에 hole이 $(p-1)$개 만큼 존재한다면, “$p$-fold connected domain“이라고 한다.
Example. integral of analytic function on doubly connected domain
doubly connected domain $D$ 위에서 analytic function $f(z)$를 적분해보자.
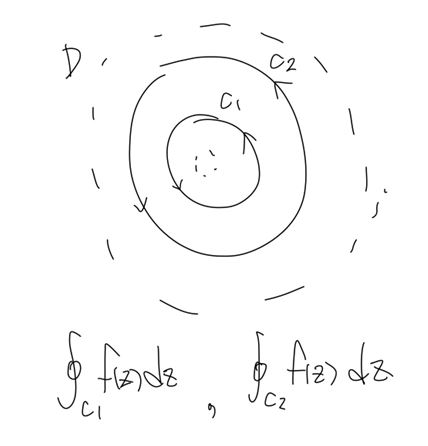
이제까지 우리는 simply connected domain 위에서의 적분을 수행했다. 하지만, 지금은 “doubly connected domain” 위에서 적분하기 때문에 앞에서 얻은 “closed integral = 0”이라는 결과를 그대로 사용할 수 없다!!
그래서 약간의 꼼수를 쓰려고 한다.
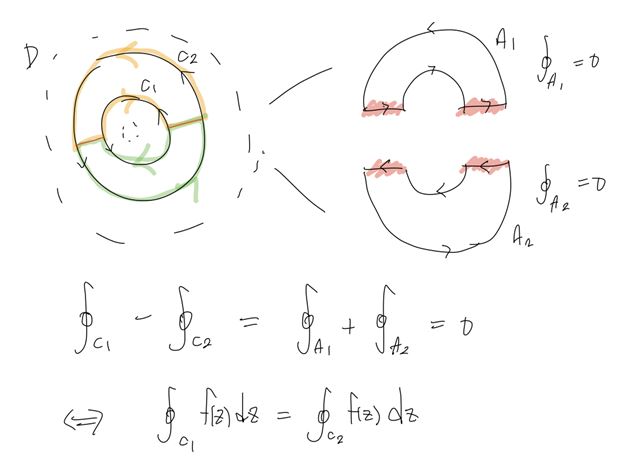
doubly connected domain 위에서의 curve $C_1$, $C_2$에서의 적분을 생각해보자. 이때, 두 curve의 사이를 적절히 분리하여 위와 같이 두 개의 curve $A_1$, $A_2$로 변형할 수 있다!
놀랍게도 $A_1$과 $A_2$는 simply connected domain 위에 있는 것으로 앞에서 쓴 Cauchy Theorem을 적용할 수 있다!!
따라서
\[\oint_{A_1} f(z) \; dz = \oint_{A_2} f(z) \; dz = 0\]이 되고, 이에 따라
\[\oint_{C_1} f(z) \; dz - \oint_{C_2} f(z) \; dz = 0\]이 되어 결국
\[\oint_{C_1} f(z) \; dz = \oint_{C_2} f(z) \; dz\]이 된다.
즉, doubly connected domain에서의 적분은 “curve와 상관없이” 모두 동일한 적분값을 얻는다!!
마찬가지 방법으로 “triply connected domain”에서는 어떻게 되는지 살펴보자.
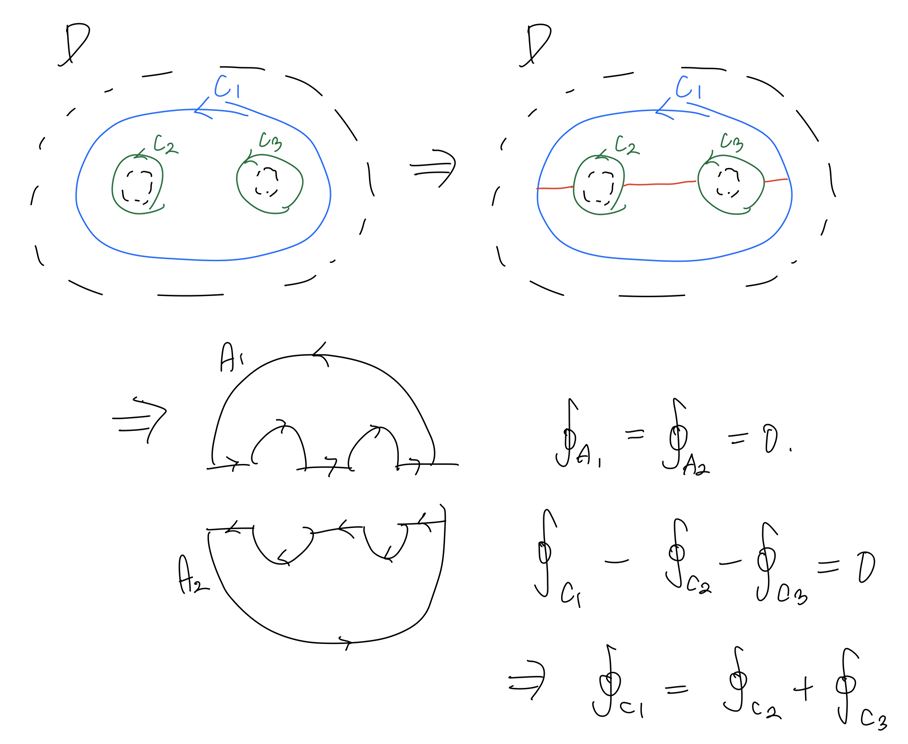
만약 위 그림의 curve $C_1$과 같이 curve 내부에 hole이 두 개가 존재하는 경우는 각 hole에서 각각 적분한 결과의 합과 동일하다.
위와 같은 사실들의 큰 장점은 analytic function에서는 적분 curve의 형태를 편의에 따라 적당히 “deformation” 할 수 있다는 것이다!!
예를 들어,
\[\oint_{C} \frac{1}{z}\;dz\]“where $C$ is a rectangle with four vertices $\pm1 \; \pm i$, CCW”라면, 우리는 rectangle curve를 적당한 disc curve로 바꾸어 아주아주 쉽게 적분을 구할 수 있다!!
Cauchy’s Integral Formula
Theorem.
Let $D$ be a simply connected domain.
Let $f(z)$ be analytic in $D$, and $z_0 \in D$.
Let $C$ be any simple closed contour in $D$ that ecloses $z_0$, CCW.
Then,
\[\oint_{C} \frac{f(z)}{z-z_0} \; dz = 2\pi i f(z_0)\]다르게 쓰면,
\[f(z_0) = \frac{1}{2\pi i} \oint_{C} \frac{f(z)}{z-z_0}\;dz\]두번째 식은 정말 놀라운게, $f(z_0)$를 contour integral로 표현했다는 점이다!!!
여기에서 좀더 변형하면, $f(z)$를 contour integral로 표현할 수도 있다.
\[f(z) = \frac{1}{2\pi i} \oint_{C} \frac{f(w)}{w-z}\;dw\]proof.
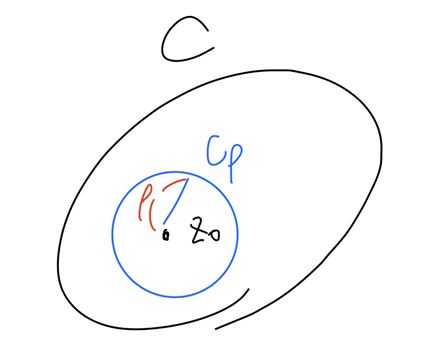
원래의 contour $C$ 내부에 “$z_0$를 중심으로 하고 반지름인 $\rho$가 충분히 작아서 $C$ 내부에 완전히 들어가는” disc $C_{\rho}$를 잡자.
첫번째로, 내부에 hole이 있는 analytic function의 적분에 의해 아래의 식이 성립한다.
\[\oint_{C} \frac{f(z)}{z-z_0}\;dz = \oint_{C_{\rho}} \frac{f(z)}{z-z_0}\;dz\]본격적으로 증명하기 전에, “직관”적으로, 덜 엄밀하게 증명을 스케치 해보자.
만약 $\rho$가 충분히 작다면, $f(z) \sim f(z_0)$가 될 것이다.
이것을 첫번째 식에 반영하면 아래와 같다.
\[\begin{aligned} \oint_{C} \frac{f(z)}{z-z_0}\;dz &= \oint_{C_{\rho}} \frac{f(z_0)}{z-z_0}\;dz \\ &= f(z_0) \oint_{C_{\rho}} \frac{1}{z-z_0}\;dz \end{aligned}\]이때, 우리는 $\oint_{C_{\rho}} \frac{1}{z-z_0}\;dz$에 대한 적분의 값은 $2\pi i$라는 것을 쉽게 알 수 있다.
\[\oint_{C_{\rho}} \frac{1}{z-z_0}\;dz = 2\pi i\]따라서,
\[\oint_{C} \frac{f(z)}{z-z_0}\;dz = 2\pi i f(z_0)\]가 되어, Theorem의 결과를 얻는다!
하지만, 이 증명은 “만약 $\rho$가 충분히 작다면, $f(z) \sim f(z_0)$가 될 것이다.”라는 부분이 명확히 증명되지 않았기 때문에 엄밀한 증명은 아니다.
그래서 좀더 엄밀하고, <극한limit>을 사용해 증명해보자.
우리가 증명하고자 하는 식은
\[\oint_{C} \frac{f(z)}{z-z_0}\;dz = 2\pi i f(z_0)\]이다.
이것을 아래와 같이 적어보자.
\[\left| \oint_{C} \frac{f(z)}{z-z_0}\;dz - 2\pi i f(z_0) \right|\]식 $\oint_{C_{\rho}} \frac{1}{z-z_0}\;dz = 2\pi i$를 이용해 위의 식을 아래와 같이 변형하자.
\[\begin{aligned} \left| \oint_{C} \frac{f(z)}{z-z_0}\;dz - 2\pi i f(z_0) \right| &= \left| \oint_{C} \frac{f(z)}{z-z_0}\;dz - f(z_0) \oint_{C_{\rho}} \frac{1}{z-z_0}\;dz \right| \\ &= \left| \oint_{C} \frac{f(z)}{z-z_0}\;dz - \oint_{C_{\rho}} \frac{f(z_0)}{z-z_0}\;dz \right| \\ &= \left| \oint_{C_{\rho}} \frac{f(z)}{z-z_0}\;dz - \oint_{C_{\rho}} \frac{f(z_0)}{z-z_0}\;dz \right| \\ &= \left| \oint_{C_{\rho}} \frac{f(z) - f(z_0)}{z-z_0}\;dz \right| \end{aligned}\]이제! 여기서 ML-ineqeuality를 적용한다!
\[\begin{aligned} \left| \oint_{C_{\rho}} \frac{f(z) - f(z_0)}{z-z_0}\;dz \right| &\le \left( \max_{z \in C_{\rho}} \; \left| f(z) - f(z_0) \right| \cdot \frac{1}{\rho}\right) \left(2\pi\rho \right) \\ &= \max_{z \in C_{\rho}} \; \left| f(z) - f(z_0) \right| \cdot 2\pi \end{aligned}\]$\rho$가 0에 가까워 질수록, $C_{\rho}: z = z_0 + \rho e^{it}$에서 $z \rightarrow z_0$가 된다.
따라서 $\left|f(z) - f(z_0)\right| \rightarrow 0$이 된다!!
즉,
\[\oint_{C} \frac{f(z)}{z-z_0}\;dz = 2\pi i f(z_0)\]가 성립한다!! $\blacksquare$
적분 curve $C$ 내부에 hole이 존재하는지 여부에 따라서 complex contour integral은 그 결과가 달라진다.
1. curve $C$ 내부에 hole이 존재하지 않음.
(= $f(z)$ is analytic inside $C$)
2. curve $C$ 내부에 hole이 존재함.
Cauchy’s Integral Formula를 적용한다.
\[\oint_{C} f(z) \; dz = \int_{C} \frac{g(z)}{(z-z_0)^n}\;dz\]