Binary Search
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Binary Search
<이분 탐색 Binary Search>. 이분 탐색은 인류 지성의 가장 직관적이고 탁월한 도구다! 정말 개인적인 의견으론, 이 알고리즘이 내가 되고, 내가 이 알고리즘이 되는 <몰아일체 物我一體> 수준에 이르기 위해 정진해야 할 정도로 “인생”에서 중요한 알고리즘이라고 생각한다.
아이디어는 간단하다. “절반으로 줄이며 탐색하기”. 나는 이걸 <관심 영역 Interest Zone>을 쳐낸다고 정의했다. 일종의 <가지 치기 Pruning>라고 생각한다는 말이다. 🌴
<분할 정복>과는 약간 스타일이 다르다고도 생각하는데, 분할 정복은 문제를 분할하고 이후에 베이스 케이스부터 다시 쌓아올려야 하지만, <이분 탐색>은 쌓아올리는 과정 없이 분할만 수행한다.
포스트의 목적이 수업 내용 정리니 일단 정리를 해보자!
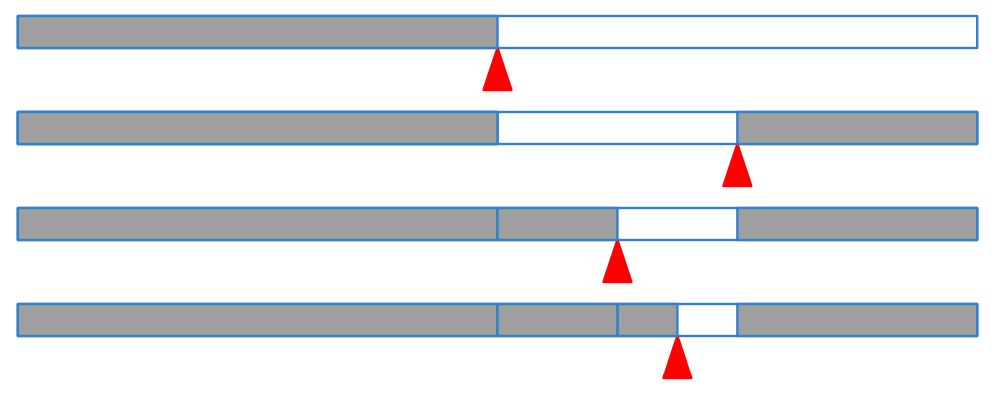
Goal: Find a key $k$ in sorted order array.
먼저 target $k$를 배열의 가운뎃 값과 비교한다. 비교 결과에 따라 좌측 절반을 취하거나 우측 절반을 취한다. 이후 그 절반에 대해서 동일한 과정을 반복한다!
<분할 정복>의 관점에서 볼 때, 단 하나의 subproblem이 발생하기 때문에 $a=1$이다. 따라서
\[T(n) = T(n/2) + O(1)\]<Master Theorem>을 적용하자. $a=1$, $b=2$, $c=0$이므로 $a/b^c = 1$이다. 따라서
\[O(1) \cdot \log n = O(\log n)\]$\blacksquare$
뭔가 이대로 포스트를 끝내기엔 아쉬워서 PS에서 흔히 하는 실수 중 하나에 대해 말해보려고 한다.
Off-by-One
“This problem could arise when a programmer makes mistakes such as using “is less than or equal to” where “is less than” should have been used in a comparison.” - Wikipedia
이분 탐색을 포함한, 대부분의 분할 정복 문제에서 “Off-be-One”은 정말 개발자를 화나게 하는 실수다!! 흔히, 하나를 덜 포함하거나 더 포함해서 생기는 실수다 😱😱
분할 정복의 경우, 유독 ceil $\lceil x \rceil$을 취할지, floor $\lfloor x \rfloor$를 취할지 헷갈리는 경우가 많다. 또는, iteratoring 과정에서 arr[0]을 포함할지나 arr[last+1]을 포함해야 하는지 등등 정말 많은 부분에서 그 “하나” 때문에 FAIL을 받게 만든다.
본인이 생각하는 이 실수를 줄이는 방법은 결국, <자기 의심 self-doubting>이다. 분할 정복으로 접근할 때, if문의 조건을 제대로 쓴 건지, 자신을 의심하는 거다. 쉽게 말하면 대충 넘어가지 말고 꼼꼼히 봐라는 말이다.
최근에 Off-by-One 때문에 시달린 문제가 있어서 링크를 걸어둔다.
Binary Search - Code
Binary Search를 구현하는 스타일은 여러 가지가 있다. 그리고 그 구현 역시 Binary Search에서 요구하는 디테일에 따라서 if문의 조건이 약간씩 변경될 수도 있다.
Binary Search를 구현하는 궁극의 템플릿이 있는 건 아니라고 생각한다. 그리고 모든 케이스에 대응하는 Binary Search 구현을 외우기는 불가능한데, 문제에서 요구하는 경우가 워낙 다양하기 때문이다.
다만, Binary Search의 기본 원형 정도는 알아두면 좋다.
Binary Search (Basic)
function binary_search(A, n, T) is
L := 0
R := n − 1
while L <= R do
m := floor((L + R) / 2)
if A[m] < T then
L := m + 1
else if A[m] > T then
R := m − 1
else:
return m
return unsuccessful
위 코드는 “정렬된 배열 $A$에서 target $T$의 index를 찾는다”는 Binary Search의 본래 목적을 충실히 수행하는 코드다. 하지만, 배열에 중복된 원소가 있어 Target $T$의 leftmost index, rightmost index를 찾는 것은 불가능하다. 이를 수행하려면 코드를 많이 수정해야 한다.
Binary Search (leftmost)
function binary_search_leftmost(A, n, T):
L := 0
R := n
while L < R:
m := floor((L + R) / 2)
if A[m] < T:
L := m + 1
else:
R := m
return L
많은 부분이 바뀌었다. 첫 시작에서 $R$은 $n-1$이 아닌 $n$부터 시작하게 되었고, return 값 역시 $L$이 되었다.
코드를 검증하기 위해 상황을 가정해보자.
A = [1, 2, 3, 4, 4, 4, 6, 6, 7, 8] (n = 10)
1. $T=-1$
배열 $A$에 $-1$의 값은 존재하지 않는다. 위 코드는 어떤 값을 뱉게 될까? 정답은 $0$이다. 항상 A[m] >= T이기 때문에 종국에는 초기에 설정한 $L$이 return 된다. 그 값은 $0$이다.
2. $T=10$
마찬가지로 배열 $A$에 $10$의 값은 존재하지 않는다. 이 경우 어떤 값을 뱉게 될까? 정답은 $10$이다. 항상 A[m] < T이기 때문에 종국에는 $L=10$, $R=10$이 되고, $L=10$이 return 된다.
3. $T=5$
배열 $A$에 $5$의 값은 존재하지 않는다. 이 경우 어떤 값을 뱉게 될까? 정답은 $5$ (A[5]=4)이다. 이때, $5$라는 값은 query $T=5$의 <rank>라고 한다. 여기서 rank는 “# of smaller elts”라는 의미로 쓰였다. 즉, leftmost를 찾는 위의 코드를 이용해서 배열 $A$ 내에서 query의 “rank”와 predecessor/successor 등등을 찾을 수 있다. Wikipedia에서는 이것을 “Approximate Matches“라는 항목에서 소개하고 있다.
Approximate Matches

<Approximate Matches>는 이진 탐색을 응용하는 가장 대표적인 방법이다! 그리고 이진 탐색을 단순히 <탐색> 기법으로만 사용하는 것은 큰 손해다! 😢
이진 탐색을 잘 사용하면, 아래와 같은 좋은 정보들을 찾을 수 있다.
- rank: the number of smaller elements
- predecessor: next-smallest element
- successor: next-largest element
- nearest neighbor
- range queries: seeking the number of elts btw two values
앞에서도 살펴봤듯이 <rank>는 “leftmost”를 찾는 알고리즘을 통해 쉽게 구할 수 있다.
반대로 <successor> query는 “rightmost”를 찾는 알고리즘을 통해 쉽게 구할 수 있다!
<range query>는 각 query $a \le b$에 대해서 $a$의 “leftmost”와 $b$의 “rightmost”를 둘다 찾음으로써 구할 수 있다. 앞에서 소개한 [BAEKJOON] 10816번 - 숫자 카드2 문제가 바로 $a=b$ 상황에서의 range query를 수행하는 문제다!
