DFS and BFS
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Definition. connected
An undirected graph is <connected> if for every pair of nodes $u$ and $v$, there is a path between $u$ and $v$.
이번 포스트를 관통하는 가장 중요한 주제는 바로 이것이다.
How to determine that a given vertex $s$ is reachable?
DFS
<DFS> 알고리즘은 <그래프 탐색>의 가장 기초가 되는 알고리즘이다. <DFS>의 아이디어는 노드 $s$에서 시작해 인접한 노드들부터 탐색하는데, 이때의 탐색은 <terminal node>를 만나거나 이미 방문한 <explored node>를 만나기 전까지 한 방향으로 계속 된다. 만약 <terminal node>나 <explored node>를 만난다면, 바로 직전에 방문한 노드로 <퇴각 Retract>한다.
위와 같은 알고리즘을 구현하기 위해서는 두 가지 요소가 필요하다.
- 방문한 노드를 기록해둘 것
- <퇴각 Retract> 하기 위해 방문 순서를 기억할 것
<DFS>는 <미로 탐색>를 탐색하는 알고리즘을 코드-레벨로 그대로 옮긴 알고리즘이다. 영웅 테세우스가 아리아드네를 구하기 위해 미노타우르스의 미로에서 밖으로 빠져나올 때, 실과 조약돌을 이용해 미로를 해매지 않을 수 있었다!! 분기점을 만났을 때 조약돌로 방문 여부를 표시하고, 퇴각 조건에선 실을 감아서 바로 직전의 분기점으로 돌아가면 미로에서 길을 잃지 않기 때문이다!! 🤩
<DFS>를 수도 코드로 표현하면 아래와 같다.
function: explore($G$, $v$)
Input: $G=(V, E)$ is a graph; $v \in V$
Output: for all nodes $u$ reachable from $v$, visited($u$) is set to $true$.
visited($v$) = $true$
for each edge $(v, u) \in E$ do
if not visited($u$) then
expolore($G$, $u$)
end if
end for
하지만 <DFS> 알고리즘이 정말로 $v$에서 reachable한 모든 노드를 방문한다고 어떻게 보장할 수 있을까? “<DFS> 알고리즘은 시작 노드 $v$에서 도달할 수 있는 모든 노드를 방문한다.”는 명제를 증명해보자!
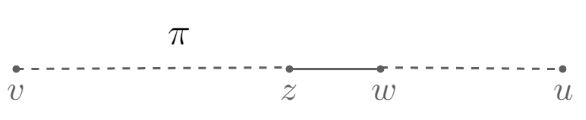
Assume $u$ is reachable from $v$ but explore misses $u$. (귀류법)
Let $\pi$ be any path from $v$ to $u$, and let $z \in \pi$ be the last vertex visited by explore.
Let $w$ be the node immediately after $z$ on path $\pi$.
When $z$ was visited, the procedure would have noticed $w$ and moved on to it.
$z$에 방문했으면, explore 함수에서 인접한 모든 노드를 방문하기 때문에 반드시 $w$도 방문할 수 밖에 없다.
하지만 explore에서 $w$를 방문했다면, 이는 처음에 가정한 $z$가 explore에서 방문한 가장 마지막 노드라는 것에 모순이다.
따라서 처음에 가정한 reachable한 $u$를 탐색하지 못 했다는 명제는 거짓이다. $\blacksquare$
이번에는 <DFS> 알고리즘의 시간 복잡도를 계산해보자! 그래프를 <인접 행렬>과 <인접 리스트>로 표현했느냐에 따라서 시간 복잡도가 다른데, 본인이 주로 <인접 리스트> 방식으로 그래프를 생각하기 때문에 여기서는 <인접 리스트>의 경우를 살펴보겠다.
그래프 $G=(V, E)$에 대해 모든 정점을 방문한다고 하면, explore는 총 $V$번 호출된다. 이때, 각 explore에서 노드 $v$의 $\deg$ 만큼 for 문을 돌리므로 <DFS> 알고리즘이 종료된 시점에서 보면, $\displaystyle \sum_{v} \deg(v)$ 만큼 iteration을 수행한 것이 된다. 이때, $\displaystyle \sum_{v} \deg(v) = 2 \times E$이다.
따라서 전체 시간복잡도는
\[O(V + 2E) = O(V + E)\]$\blacksquare$
BFS
<BFS> 알고리즘도 <DFS> 알고리즘과 마찬가지로 노드 $s$가 reachable 한지를 판단하는 알고리즘이다. 하지만, <BFS>의 경우 reachable 판단 작업보다도 노드 $s$부터의 <거리 distance>를 재는 데에 탁월한 알고리즘이다!!
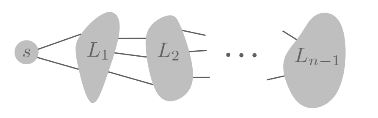
<BFS>의 컨셉은 “layer by layer“다. 시작 노드 $s$로부터 인접한 모든 노드를 살피고; 1st layer, 그리고 그 1st layer의 노드들로부터 인접하지만 방문하지 않은 다른 모든 노드를 살피고; 2nd layer, … 더이상 방문할 노드가 없을 때까지 이 방식으로 모든 노드를 순회한다. 이제 각 노드가 몇번째 layer에 속해있는지를 통해 $s$로부터의 <거리>를 측정할 수 있다!! 어떻게 보면, 이산 영역에서 <interest circle>의 반지름을 1씩 들리며 거리를 측정해가는 과정처럼 보이기도 한다.
<BFS>를 수도 코드로 표현하면 아래와 같다.
function: bfs($G$, $s$)
Input: $G=(V, E)$ is a graph; $s \in V$
Output: for all nodes $u$ reachable from $s$, $\textsf{dist}(u)$ = distance from $s$ to $u$.
for asll $u \in V$ do
$\textsf{dist}(u) = \infty$
end for
$\textsf{dist}(s) = 0$
$Q = [s]$ (queue containing start node $s$)
while $Q$ is not empty do
$u=Q.\textsf{pop}()$
for all edges $(u, v) \in E$ do
if $\textsf{dist}(v) = \infty$ then
$Q.\textsf{push}(v)$
$\textsf{dist}(v) = \textsf{dist}(u) + 1$
end if
end for
end while
<BFS> 알고리즘의 시간 복잡도는 $V$개 만큼의 노드를 방문하고, 각 노드에 대해서 모든 인접한 노드를 방문하기 때문에, <DFS> 알고리즘과 마찬가지로 $O(V + E)$이다.
<\DFS>, <BFS> 알고리즘은 그래프 자료형을 다루는데 기초가 된다. 사실 인간이 생각하는 방식을 그대로 옮긴 알고리즘이라 그렇게 어렵진 않다 ㅎㅎ 😆
본 포스트에서 연관되는 내용은 아래와 같다.
1. DFS & BFS - code 💻
알고리즘을 이해하는 것도 중요하지만, 그것을 코드로 구현하는 것 역시 중요하다! 본인의 <DFS>, <BFS> 코드 스타일은 아래의 링크에서 볼 수 있다.
2. DFS Tree 🌲
<DFS> 알고리즘으로 그래프를 순회하면 방문 순서를 바탕으로 <Tree> 구조를 만들 수 있다!! 이 <DFS Tree>는 나중에 <DAG; Directed Acyclic Graph>를 판단하는 문제와도 연관된다.
👉 DFS Tree
3. Dijkstra Algorithm 🚗
<BFS> 알고리즘을 통해 노드와 노드 사이의 거리를 측정할 수 있게 되었다. 하지만, edge 사이에 weight 값이 부여되어 있다면, <BFS>로 구한 거리가 노드와 노드 사이의 최단 거리는 아니다. <Dijkstra Algorithm>은 <Weighted Graph>에서 최단 거리를 구하는 알고리즘이다!
