Linear Classification - 1

2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

Classficiation by Linear Regression

Binary Classification

Assume that $\mathcal{Y}= \{ 0, 1 \}$, and consider the <linear regression> model

\[Y = X^T \beta + \epsilon\]

For some estimator $\hat{\beta}$, and given $X=x$, predictor $Y$ do something like this

\[\hat{Y} = \begin{cases} \quad 1 & \text{if } x^{T}\hat{\beta} > 0.5 \\ \quad 0 & \text{if } x^{T}\hat{\beta} \le 0.5 \end{cases}\]

이때, $x^T \hat{\beta}$는 $Y=1$에 대한 확률을 뱉는 함수의 일종이라고 생각할 수 있다.

\[\hat{f}(x) = \text{Pr}(Y = 1 \mid X = x) = E(Y \mid X = x)\]

이련 형태의 각 Class에 대한 posterior probability를 계산해 Classify를 진행하는 모델을 <Bayes Classifier>라고 통칭한다.

Multi-class Classification

Assume that $\mathcal{Y}=\{1, \dots, K\}$, and let $\mathbf{Y}$ be the $n \times K$ binary matrix where the $(i, k)$ element is $1$ if $y_i = k$ and $0$ otherwise.

Let

\[\hat{\mathbf{B}} = (\mathbf{X}^T\mathbf{X})^{-1} \mathbf{X}^T\mathbf{Y}\]

(deriven from RSS estimator!)

\[\hat{\mathbf{Y}} = \mathbf{X} \hat{\mathbf{B}}\]

이렇게 둔다면 inference에서는, For $X=x$, one may predict $Y$ as

\[\hat{Y} = \underset{k\in\mathcal{Y}}{\text{argmax}} \; {\hat{f}_k (x)}\]

where $(\hat{f}_1 (x), \dots, \hat{f}_K(x)) = x^T \hat{\mathbf{B}}$.

이때, 각 $\hat{f}_i (x)$는 binary classification의 $\hat{f}(x)$와 비슷하게 아래의 조건부 확률 또는 poster-priority를 예측하는 estimator의 역할을 한다.

\[\hat{f}_k (x) = \text{Pr}(Y=k \mid X=x)\]

Problem.

(추후에 기술)

---

Probabilistic Model

위의 두 경우에서 살펴봤듯, Linear Regression에 의한 접근은 결국 아래의 조건부 확률을 estimate 하는 접근이었다.

\[\text{Pr}(Y=k \mid X=x)\]

이때, 이 조건부 확률은 posterior probability로 <베이즈 정리>에 의해 아래와 같다.

\[\text{Pr}(Y=k \mid X=x) = \frac{\pi_k \cdot f_k(x)}{\displaystyle \sum^K_{i=1} \pi_i \cdot f_i (x)}\]

이때, 우변의 각 항목들을 살펴보면

• $\pi_k$: the <class probability> of class $k$; prior probability

\[\pi_k = P(y=k)\]

• $f_k (x)$: the <class-conditional density> of $X$ in class $Y=k$

\[f_k (x) = P(X=x \mid Y=k)\]

만약 우리가 $\pi_k$, $f_k (x)$를 모두 알고 있다면, 우리는 $X=x$가 있을 때, 어떤 $Y=k$가 선택되어야 하는지 estimate 할 수 있다. 단, $\pi_k$, $f_k(x)$는 모두 우리가 추정해야 하는 값이며, 이것을 추정하기 위해 어떻게 접근하고 어떤 가정을 쓰는지 수업에서 배운다.

Linear Discriminant Analysis

LDA는 $f_k$가 아래와 같은 정규 분포 $N(\mu_k, \Sigma_k)$를 따른다고 가정한다. ¹

\[f_k(x) = \frac{1}{\left| 2\pi \Sigma_k \right|^{1/2}} \exp \left[ - \frac{(x-\mu_k)^T \Sigma_k^{-1} (x-\mu_k)}{2}\right]\]

이때, 만약 각 $\Sigma_k$에 대해

\[\Sigma_k = \Sigma \quad \text{for all} \; k\]

라는 아주아주 특별한 가정이 추가된 것이 <LDA; Linear Discriminant Analysis>다! 😍

위와 같이 설정했을 때의 <decision boundary>를 생각해보자.

\[P(Y=k \mid X=x) = P(Y=l \mid X=x)\]

boundary에 대한 위의 식을 잘 정리해보면,

\[\begin{aligned} \log \frac{P(Y=k \mid X=x)}{P(Y=l \mid X=x)} &= \log \frac{\pi_k \cdot f_k(x)}{\pi_l \cdot f_l(x)} = \log \frac{\pi_k}{\pi_l} + \log \frac{f_k(x)}{f_l(x)} \\ &= \log \frac{\pi_k}{\pi_l} + \log \left( \frac{\exp\left( -\frac{(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)}{2}\right)}{\exp\left( -\frac{(x-\mu_l)^T\Sigma^{-1}(x-\mu_l)}{2}\right)}\right) \\ &= \log \frac{\pi_k}{\pi_l} + \log \left( \exp \left( \frac{-(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)+(x-\mu_l)^T\Sigma^{-1}(x-\mu_l)}{2}\right) \right) \\ &= \log \frac{\pi_k}{\pi_l} + \left( \frac{-(x-\mu_k)^T\Sigma^{-1}(x-\mu_k)+(x-\mu_l)^T\Sigma^{-1}(x-\mu_l)}{2}\right) \\ &= \left(\log \frac{\pi_k}{\pi_l} -\frac{1}{2} (\mu_k + \mu_l)^T\Sigma^{-1}(\mu_k - \mu_l)\right) + x^T \Sigma^{-1} (\mu_k - \mu_l) \\ &= a + b^T x = 0 \end{aligned}\]

일부 스텝은 과정을 생략하고 결과만 바로 적었는데, 자세한 과정은 아래의 펼쳐보기에 기술해두겠다.

펼쳐보기

(추후 기술)

위의 스텝의 마지막에 $a+b^Tx = 0$라는 평면식이 유도 되었는데, 결국 이 $a+b^T x = 0$이라는 hyper-plain이 <decision boundary>가 됨을 알 수 있다!!

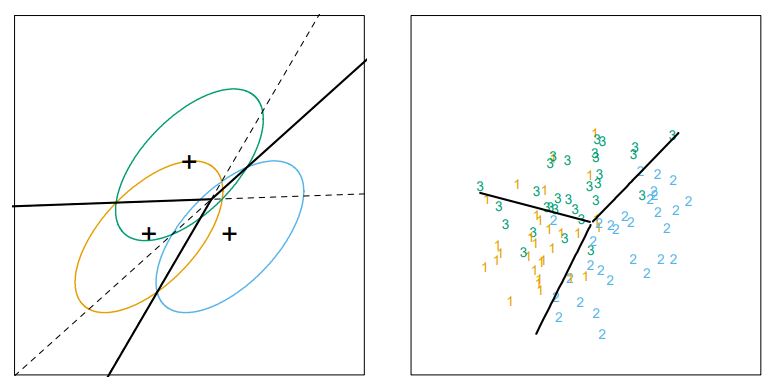
Classification.

이제 LDA를 이용해 classification을 어떻게 수행하는지 논해보자.

먼저 $P(Y = k \mid X=x)$에서 분모가 모두 동일한 값을 가질 테니, 분자인 $\pi_k \cdot f_k(x)$를 maximize하면 된다! $f_k(x)$에 지수식이 있으니 계산의 편의를 위해 $\log$를 씌워주자.

\[\delta_k (x) = \log P(Y = k \mid X=x) = \log \pi_k + x^T \Sigma^{-1} \mu_k - \frac{1}{2} \mu_k^T \Sigma^{-1} \mu_k\]

이때, $\log P(Y = k \mid X=x)$를 <linear discriminant function> $\delta_k (x)$라고 부른다. 우리는 $\{\delta_k(x)\}_{k \in \mathcal{Y}}$에 대해 $\text{argmax}$를 취해

\[\hat{y} = \underset{k \in \mathcal{Y}}{\text{argmax}} \; \delta_k (x)\]

가장 큰 discriminant function $\delta_k(x)$ 함수값을 갖는 클래스로 classification을 진행한다!

Parameter Estimation.

아직 우리는 $\pi_k$와 $f_k(x)$를 정확히 정의하지는 않았다. $f_k(x)$가 normal dist. $N(\mu_k, \Sigma)$를 따른다고 가정은 했지만, $\mu_k$, $\Sigma$에 대한 명확히 정의하지는 않았었다. 이번 파트에서는 모델 파라미터들을 어떻게 추정할 수 있는지 살펴본다.

Let $\displaystyle n_k = \sum^n_{i=1} I(y_i=k)$, then

\[\hat{\pi}_k = \frac{n_k}{n} \quad \text{(sample proportion)}\] \[\hat{\mu}_k = \frac{1}{n_k} \sum_{i: y_i = k} x_i \quad \text{(sample mean)}\] \[\hat{\Sigma} = \frac{1}{N-k} \sum^K_{k=1} \sum_{i: y_i=k} (x_i - \hat{\mu}_k) (x_i - \hat{\mu}_k)^T \quad \text{(pooled sample cov-var matrix)}\]

펼쳐보기

1. $\mu$를 확실히 알 때

\[\hat{\Sigma} = \frac{1}{N} \sum^K_{k=1} \sum_{i: y_i=k} (x_i - \mu_k) (x_i - \mu_k)^T\]

2. $\mu$를 모를 때

\[\hat{\Sigma} = \frac{1}{N-k} \sum^K_{k=1} \sum_{i: y_i=k} (x_i - \hat{\mu}_k) (x_i - \hat{\mu}_k)^T\]

Quadratic Discriminant Analysis

LDA에서는 각 class $k$의 Cov-Var matrix $\Sigma_k$가 모두 같은 값을 가진다고 가정했다. 그런데 만약 이 가정을 제거한다면, 우리는 <QDA; Quadratic Discriminant Analysis>를 하게 된다.

\[\delta_k (x) = \log \pi_k - \frac{1}{2} \log \left| \Sigma_k \right| - \frac{1}{2} (x-\mu_k)^T \Sigma_k^{-1} (x-\mu_k)\]

LDA에서의 $\delta_k(x)$와 비교해면, QDA의 경우, cancel out이 덜 되기 때문에 “2차식”이 남게 된다!

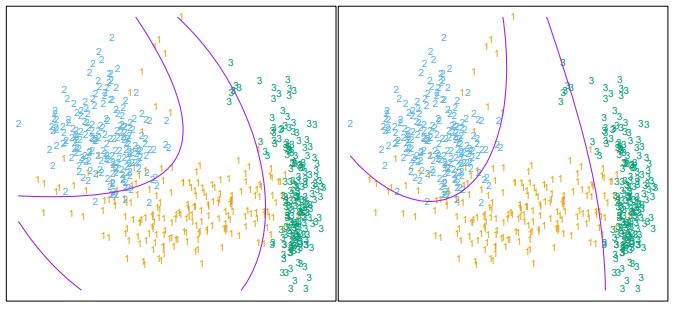
(둘 중 하나는 QDA를, 다른 하나는 $X_i$에 대한 2차식($X_i^2, X_iX_j$)을 넣고 LDA를 돌린 결과다.)

---

이어지는 포스트에서는 <Logistic Regression>에 대해 다룬다. 좀더 익숙한 용어를 쓰자면, <MLE; Maximum Likelihood Estimation>에 대해 다룬다는 말이다!

👉 Linear Classification - 2

---

1. 강조하지만, 반드시 이렇게 모델링할 수 있는 건 아니다. $f_k(X)$의 분포가 $N(\mu_k, \Sigma_k)$를 따른다고 ‘가정’했을 뿐이다! 실제 $f_k(X)$의 분포는 다를 가능성이 크다! ↩