Bellman-Ford Algorithm
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
💥 <Bellman-Ford Algorithm>은 negative edge가 있는 Acyclic Directed Graph에서의 Shortest path를 찾는 알고리즘입니다. 만약 negative cycle이 있다면, <Bellman-Ford Algorithm>을 쓸 수 없습니다 😥
Shortest Path with Negative Edge
<Dijkstra’s Algorithm>은 아래의 Invariant를 갖는다.
The shortest path from the starting point $s$ to any node $v$ must pass exclusively through nodes that are closer than $v$.
이때, “pass exclusively”는 $s$ to $v$의 shortest path가 각 노드를 단 한 번씩만 방문한다는 말이다! 이 성질은 그래프에 positive edge만 존재한다면, 성립한다. 하지만, negative edge가 존재한다면, negative cycle에 의해 이미 방문한 노드를 한번 더 방문할 가능성이 있고, 이것은 “pass exclusive”를 위배한다!
Golden rule for the shortest path
shortest path에는 다음의 중요한 성질이 있다.
- Shortest path is one branch of path tree.
update()gives the correct dist($v$) value when- $u$ is the second-last node of the shortest path to $v$.
- dist($u$) is correctly set.
위의 두 성질로부터 Bellman-Ford 알고리즘을 어떻게 유도하는지 살펴보자.
Shortest path is one branch of path tree
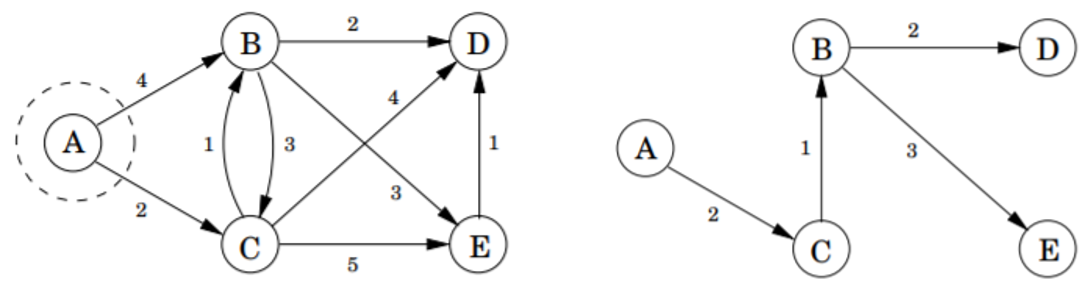
Graph and its Shortest path tree
diagram from 『Algorithms(Dasgupta)』
Graph가 Negative Cycle을 갖지 않는다면, Graph의 shortest path는 Shortest Path Tree를 이룬다.
distance update rule
procedure update((u, v) ∈ E)
if dist(v) > dist(u) + w(u, v):
dist(v) = dist(u) + w(u, v)
update()1 gives the correct dist($v$) value when
- $u$ is the second-last node of the shortest path to $v$.
- dist($u$) is correctly set.
Proof.
Consider the shortest path $\pi = su_1u_2u_3\cdots u_k t$ from $s$ to $t$.
Then every subpath $\pi_i = su_1\cdots u_i$ is
(1) the shortest path from $s$ to $u_i$, otherwise we can decrease $\texttt{dist}(t)$
(2) it is simple! otherwise there is a cycle, and we can still decrease $\texttt{dist}(t)$
위의 두 명제를 다시 기술하면, “the shortest path from $s$ to $u_i$ consists of exactly $i$ edges.”
위의 사실에 의해 $\texttt{u_1}$의 경우를 생각했을 때, $u_1$은 그래프에 존재하는 모든 edge에 대해 맨처음 update 했을 때, 그 값이 final value로 설정된 경우일 것이다.
이런 $\texttt{dist}$ update 과정을 반복해서, $i$번 진행한다면, $\texttt{dist}(u_i)$까지는 final value가 제대로 설정될 것이다. (귀납법이다, 귀납법!)
위와 같은 원리에 의해 우리가 원하는 노드에까지 final value를 설정하려면, shortest path의 최대 길이인 $V-1$번 만큼 이 update 과정을 반복하면 된다! $\blacksquare$ 😆
이제 Bellman-Ford 알고리즘에서 이 명제를 어떻게 활용하는지를 살펴보자!
Algorithm.
시작점 $s$는 $\texttt{dist}(s)=0$으로, 나머지 노드는 모두 INF로 초기화한다. 이제 시작점 $s$와 연결된 노드들을 살펴보자. See node $u_i$ s.t. $(s, u_i) \in E$
$\texttt{dist}(u_i)$의 값은 update() 규칙에 따라 $\texttt{dist}(u_i) = \texttt{dist}(s) + w(u_i, v)$가 된다. 위의 명제를 다시 보자. 만약 $\texttt{dist}(u_i)$에 대해 $s$가 second last 노드이고, $\texttt{dist}(s)$가 correctly set라면, $\texttt{dist}(u_i)$에는 update()를 통해 shortest distance가 저장된다.
이제, 모든 edge $E$에 대해서 update() rule을 적용해보자. $\texttt{dist}(s)$ 외에는 모두 INF로 초기화 되어 있기 때문에 $s$와 연결된 노드들의 $\texttt{dist}$ 값만 갱신된다. 이때에 갱신되는 노드들 중 적어도 하나는 $s$를 second last 노드로 갖는다.2
따라서 첫 iter의 update()를 통해 correctly set된 노드 몇개가 추가된다.
Shortest Path Tree는 트리의 성질에 따라 $V-1$ 만큼의 edge를 갖는다. iter 한번에 shortest path의 한 간격을 커버하는 것이므로 우리는 $V-1$번의 iter이 필요하다! (또는 앞의 증명에서 언급한대로, shortest path의 최대 길이인 $V-1$번 만큼 iter한다.)
Finding Negative Cycle
Bellman-Ford 알고리즘은 Negative edge를 허용하지만, Negative Cycle은 허용하지 않는다. 그래서 Bellman-Ford 알고리즘의 결과를 보장하기 위해선 그래프에 Negative Cycle이 없음을 확인해야 한다!!
그래서 만약 $V-1$번 ieteration을 진행한 후 한 번 더 iteration을 진행했을 때에도 update() 함수가 호출된다면, 주어진 그래프에 Negative Cycle이 있다고 판단한다.
맺음말
Dijkstra 알고리즘과 달리 Bellman-Ford 알고리즘은 그 원리가 한번에 잘 와닿지 않는 것 같다. 하지만 실전에선 positive edge만 나오는 것은 아니기 때문에 negative edge 경우도 늘 준비해야 한다. 🤩
