DAG & Topological Sort

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

---

<DAG; Directed Acyclic Graph>는 cycle이 존재하지 않는 directed graph를 말한다.

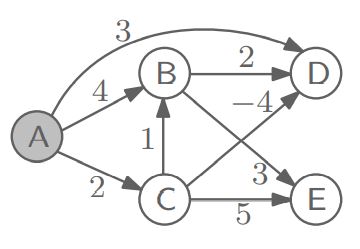
이때, 모든 DAG의 노드는 <topological ordering>를 가지기 때문에, 우리는 DAG를 <topological sort>로 linearization 할 수 있다!!

이것은 DAG가 갖는 성질 때문인데, “Every DAG has at least one vertex with no incoming edge.”이기 때문이다! 이 성질에 따라, <topological sort>는 DAG에 존재하는 vertex with no incoming edge를 하나씩 제거해가면서, DAG를 linearization 한다 🤩

위에서 제시한 DAG에 대해 vertex with no incoming edges를 반복적으로 제거하여 topological sort를 수행하면, 그 결과는 아래와 같다.

DAG과 topological ordering 사이의 관계를 기술하면 아래와 같다.

A directed graph is a DAG iff it has a topological ordering.

---

이렇게 DAG를 topological order로 linearization 했다면, 우리는 DAG 위에서의 shortest path를 쉽게 구할 수 있다.

Linearize $G$

for each $u \in V$ in linearized order
  for all edges $(u, v) \in E$
    $\texttt{update}(u, v)$
  end for
end for

참고로 주어진 그래프가 DAG라면, negative edge가 있어도 위와 같은 방식으로 충분히 shortest path를 구할 수 있다!! (DAG는 cycle이 없기 때문에, negative cycle에 대한 걱정이 없다! 😆)

---

여기까지가 정규 수업에서 다룬 <Graph Algorithm>에 대한 내용이다. 그래프 이론은 PS의 기본이기 때문에 이곳에서 다룬 모든 내용을 완전히 이해하고 언제든지 쓸 수 있도록 하는게 중요한 것 같다. ‘알고리즘’ 과목의 정규 수업에서 다루지는 않았지만, ‘인고지능’ 과목에서는 다뤘던 heuristic path finding 기법인 <A* Algorithm>도 추후에 다뤄보도록 하겠다.

그래프에 대한 내용은 나중에 <Network Flow> 부분에서 다시 등장한다! 😉