Edit Distance

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

---

두 string 사이의 거리를 측정하는 방법이 있을까? 가장 쉬운 방법은 두 string이 같은 문자로 aligned 되도록 매칭해 어긋나는 문자의 숫자로 거리를 매길 수 있다.

이때, align 하는 방식에 따라, 두 string 사이의 거리가 달라질 수 있다. 그래서 가능한 모든 align 방식 중 가장 작은 <cost>를 <edit distance>라고 정의한다.

주어진 두 string 사이의 <edit distance>를 어떻게 측정할 수 있을까? DP를 사용하면, 정말 쉽게 <edit distance>를 구할 수 있다!!

DP로 접근하기 위해 먼저 문제를 subproblem으로 분할해야 한다. 이때, 우리가 가장 자연스럽게 생각해볼 수 있는 분할 방식은 두 string을 prefix로 분할하는 방법이다.

Given two strings, $x[1, \dots, m]$ and $y[1, \dots, n]$. A good subproblem would be to compute the optimal edit distance btw some prefixes, $x[1, \dots, i]$ and $y[1, \dots, j]$.

Let $E(i, j)$ be the optimal edit distance btw two prefixes. Then

\[E(i, j) = \min \begin{cases} E(i-1, j) + 1 \\ E(i, j-1) + 1 \\ E(i, j) + \texttt{diff}(i, j) \end{cases}\]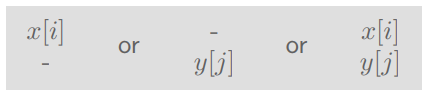

아이디어는 간단하다. 두 prefix에 대해, 마지막 문자가 공백일 때의 두 경우와 마지막 문자를 맞췄을 때의 경우를 종합해 최소 edit distance의 경우를 취하는 아이디어다!

// initialization
for $i=0, 1, 2, \dots, m$
  $E(i, 0) = i$

for $j=0, 1, 2, \dots, n$
  $E(0, j) = j$

// dp process
for $i=1, 2, \dots, m$
  for $j=1, 2, \dots, n$
    $E(i, j) = \min \{ E(i-1, j) + 1, \; E(i, j-1) + 1, \; E(i-1, j-1) + \texttt{diff}(i, j)\}$

return $E(m, n)$

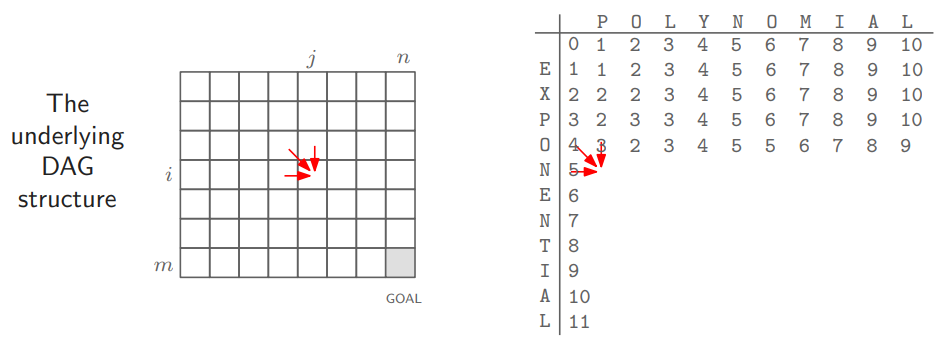
<Edit Distance> 문제는 두 string의 idx를 사용하기 때문에 2차원 DP를 사용한다. 그리고 위의 그림에서도 볼 수 있듯 <Edit Distance>에서는 DAG 구조가 있다!

---

<edit distance>는 문자열 사이의 거리를 정의하는 좋은 기준이 된다. 그렇기 때문에 문자열 문제가 자주 등장하는 코딩 테스트에서도 빈출이 되는 주제이므로 늘 숙지해둬야 하는 알고리즘이라고 생각한다 😁

<edit distance>는 “삽입”, “삭제”, “교체”의 세 가지 연산을 통해 최소 편집 거리를 계산한다. 이때, 인접한 두 글자끼리 교환하는 “교환(transposition)” 연산이 추가되는 경우가 <Damerau-Levenshtein distance>다. 내용과 코드를 포스트로 정리했으니, 문자열 거리에 대해 더 관심이 있다면, 아래의 포스트를 추천한다! 😉

👉 Damerau-Levenshtein distance

추천 문제

• 최소 편집