Interval Scheduling and Partitioning
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Interval Scheduling
각 Job $j$는 $[s_j, f_j]$의 start time, finish time을 가진다고 가자. 이때, 두 Job이 compatible 하다는 것은 두 Job이 서로 중첩되지 않는다는 말이다. <Interval Scheduling>은 전체 Job의 집합의 부분집합 중 포함된 모든 Job이 서로 compatible하면서 그 부분집합의 크기가 최대가 되는 집합을 찾는 것을 목표로 한다.
과연 위와 같은 Maximum compatible subset을 찾으려면 어떻게 해야할까?? Greedy Algorithm은 모든 Job을 finish time으로 정렬한 후에 종료시간이 빠르면서 compatible 한 순서대로 고르는 방식을 제안한다.
Theorem.
<Interval Scheduling> 문제에서 위와 같은 Greedy Approach는 optimal solution을 보장한다.
Proof.
(귀류법) Assume that the given greedy approach is not optimal.
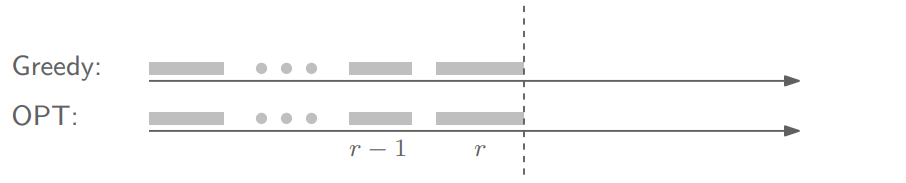
Let $i_1, i_2, \dots, i_n$ denote the set of jobs selected by greedy.
Let $j_1, j_2, \dots, j_m$ denote the set of jobs in the optimal solution with $i_1 = j_1$, $i_2 = j_2$, …, $i_r = j_r$ for the largest possible value of $r$.
(해설) 즉, greedy가 optimal이 아니고, 다른 optimal sequence $\{ j_k \}$가 존재하는데, 그 optimal seq.와 greedy seq.가 $r$까지는 동일한 seq.라고 가정한다는 말이다.
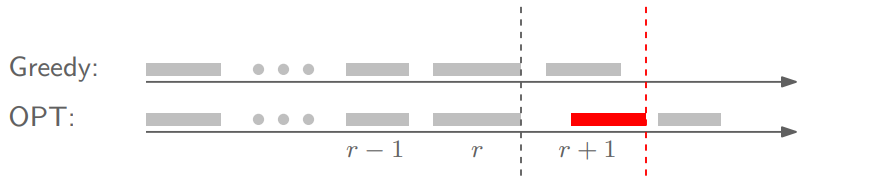
By the greedy choice, job $i_{r+1}$ finishes before $j_{r+1}$.
(처음에 greedy approach가 optimal이 아니라고 했으므로 위와 같은 상황이 성립한다!)
So in the optimal solution, we can replace job $j_{r+1}$ with job $i_{r+1}$. The resulting solution is still feasible and optimal, but contradicts the maximality of $r$.
(즉, 우리가 greedy가 아닌 다른 optimal seq.를 가정했을 때, 쓴 maximality 가정이 흔들리기 때문에 “greedy seq.가 optimal 아니다”라는 가정은 거짓이 된다는 말이다.)
Interval Partitioning
$n$개의 수업이 주어졌고, 각 수업 $j$는 $[s_j, f_j]$의 start/finish time을 갖는다고 하자. 이때, 어떤 두 수업도 겹치지 않도록 스케쥴링 하면서, 강의실의 갯수는 최소가 되는 방법을 생각해보자!
위의 문제 역시 Greedy Algorithm으로 간단히 해결할 수 있다!!
Algorithm: Interval-Partition($S$)
// initialization
sort intervals by starting time.
$d=0$
// greedy process!
for $j=1$ to $n$
if lecture $j$ is compatible with classroom $k$
schedule lecture $j$ in classroom $k$
else
allocate a new classroom $d+1$
schedule lecture $j$ in a new classroom
$d = d+1$
이때, 각 classroom $k$는 현재 lecture의 finish time $f_j$를 담고 있어야 한다. 그래서, 이것을 classroom을 Priorirty Queue로 관리하여, 만약 새로운 lecture가 front node의 finish time보다 빠른 start time을 가진다면, $d = d+1$ 한 후에 Priority Queue에 새롭게 insertion 하면 된다!