Chain Matrix Multiplication

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

---

일반적으로 행렬 곱셈 $A_1 \times A_2 \times \cdots \times A_n$은 Associative 하기 때문에 행렬의 곱셈 순서를 어떻게 진행하느냐에 따라서 전체 연산의 수가 달라진다.

예를 들어,

• $A: 50 \times 20$
• $B: 20 \times 1$
• $C: 1 \times 10$
• $D: 10 \times 100$

4가지 행렬이 있을 때,

• $A \times ((B \times C) \times D) = 120,200$
• $(A \times B) \times (C \times D) = 7,000$

이 된다. 즉, 행렬의 곱셈 순서를 잘 조정해 필요한 연산의 수를 줄일 수 있다는 것이다!!

---

naive approach

가장 간단하지만, 가장 비용이 많이 드는 방법은 모든 행렬 곱셈 순서를 모두 살펴보는 것이다. 행렬의 곱셈은 binary operation이기 때문에 전체 행렬 연산은 어떤 binary tree의 형태로 표현할 수 있다. 이때, 우리는 $n$개의 행렬을 가지고 있기 때문에, 이 binary tree는 $n$개의 leaf node를 가진 트리가 된다. 또한, 그 가짓수는 exponentially many한 $2^n$개가 된다.

---

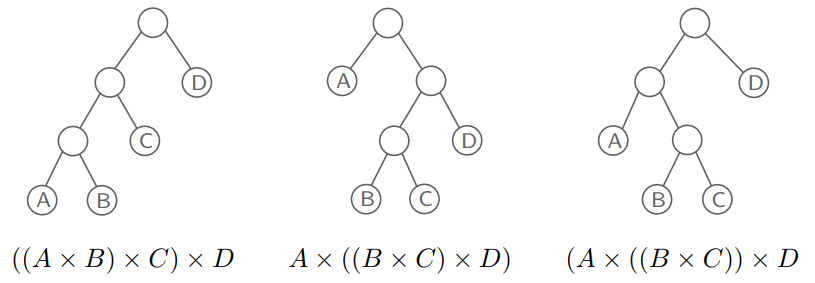
Dynamic Programming

DP에서는 이 문제를 아래와 같이 접근한다.

"For a tree to be optimal, its subtree must also be optimal!"

다른 곳에서는 부분수열(sebsequence)을 이용해 문제를 해결한다고도 설명한다.

1. 전체 수열을 길이 2의 부분 수열로 분리한다.
2. 길이 2의 부분 수열에서 (최소) 비용을 구한다.
3. 길이 3의 부분 수열을 살펴본다. 이때, 길이 2의 부분 수열에서 구한 비용을 바탕으로 최소 비용을 구한다.
4. 길이 4는 길이 3에서 구한 최소 비용을 바탕으로 최소 비용을 구한다.
5. 이 과정을 길이 $n$까지 반복

이 과정을 정리해 기술하면,

• $C(i, j)$ = min cost of multiplying $A_i \times \cdots A_j$

for $\ell = 1, 2, \dots, n$
  for $i=1, 2, \dots, n - \ell + 1$
    $j = i + \ell$
    for $k=i, \dots, j-1$
      $\texttt{cost} = C(i, k) + C(k+1, j) + m_{i-1} \times m_k \times m_j$
      $C(i, j) = \min \{ C(i, j), \; \texttt{cost}\}$

return $C(1, n)$

위의 과정을 그림으로 표현하면 아래와 같이 표현할 수 있다.

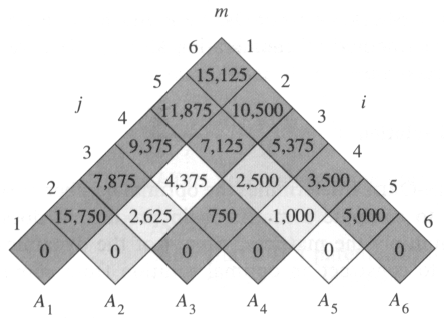
Image from here

만약 best-split 순서를 기록해 실제 binary opr tree를 구성하고 싶다면, $C(i, j)$를 갱신하는 과정에서 언제 minimum을 달성하는지 기록해두면 된다.

      if $\texttt{cost} < C(i, j)$
        $C(i, j) = \texttt{cost}$
        $S(i, j) = k$

그리고 binary opr tree를 재현할 때는 $S(1, n)$으로 splitting point를 찾고, 그리고 $S(1, k)$, $S(k, n)$의 값으로 그 다음 splitting point을 찾고, … 이런 식으로 진행하면 된다 😁

---

추천 문제

• 11049번: 행렬 곱셈 순서
• 11066번: 파일 합치기

---

참고자료

• ‘마이구미’님의 포스트