Implementations of Heap

이 포스트는 위키피디아의 Heap(data structure)에 소개된 Heap의 구현들을 다룹니다. 지적과 조언은 언제나 환영입니다 ㅎㅎ

이번 포스트에서는 <Heap>의 구현 방식을 살펴볼 예정입니다. 구현 코드는 추후에 별도의 포스트에서 Heap의 종류별로 다룰 예정입니다! 😁

<Binomial Heap>에서부터 시간복잡도를 유도하기 위해 amortized analysis를 사용합니다. “Amortized Analysis” 포스트를 먼저 읽고 오길 권합니다 😉

---

<Priority Queue>의 구현인 <Heap>은 많은 알고리즘에서 핵심적인 역할을 한다. 보통 Binary Tree로 구현하는 <Binary Heap>을 많이 알테지만, 정규 수업이나 위키피디아의 문서를 살펴보면 <Binary Heap> 외에도 여러 형태의 <Heap>에 대한 구현이 존재한다!! 이번 포스트에선 이 <Heap>의 구현에 대해 자세히 알아볼 예정이다. 😎

• Heap by unordered array
• Heap by ordered array
• Binary Heap
• d-ary Heap
• Binomial Heap
  • Binomial Tree
• Lazy-Binomial Heap
• Fibonacci Heap

---

Unodered Array & Ordered Array

min 또는 max에 빈번히 접근하는 priority queue를 배열로 naive 하게 구현하는 방식이다. 정말 아무런 테크닉을 사용하지 않았기 때문에 쿼리가 들어올 때마다 linear search 또는 binary search를 통해 쿼리를 해결한다.

Unordered Array.

• $\texttt{getMin}$: $O(N)$
  • 선형 탐색으로 min 찾아서 리턴
• $\texttt{insert}$: $O(1)$
  • 그냥 배열의 맨 뒤에 붙이면 OK
• $\texttt{deleteMin}$: $O(N)$
  • 선형 탐색으로 min 찾음 $O(N)$
  • 배열이므로 삭제에 $O(N)$ 소요

Ordered Array.

원소가 하나 추가될 때마다 정렬해 Ordered 구조를 유지. 이때, min-heap이라면, min이 배열 맨 끝에 있는 구조여야 한다. // 그 이유는 min이 배열 맨 앞에 있게 되면, $\texttt{deleteMin}$에서 손해임. 직접 비교해보면 금방 이해가 된다.

• $\texttt{getMin}$: $O(1)$
  • 맨 뒤에 있는 min 원소를 리턴
• $\texttt{insert}$: $O(N)$
  • 이진 탐색으로 자신의 위치를 찾음 $O(\log N)$.
  • 배열이므로 삽입에 $O(N)$ 소요.
• $\texttt{deleteMin}$: $O(1)$
  • 맨 뒤에 있는 min 원소를 삭제. 맨 뒤의 원소를 없애므로, $O(1)$

---

Binary Heap

일반적으로 배우는 <Heap> 자료구조이다. <완전 이진 트리; Complete Binary Tree>라는 트리 구조로 구현된다. 사실 완전 이진 트리라고 별게 있는게 아니라 배열로 구현된 Binary Tree에서 부모-자식 사이의 관계가

• 부모 → 자식: $k$ → ($2k$ & $2k+1$)
• 자식 → 부모: $k$ → $k/2$

인 구조일 뿐이다. 다만, 이 구조일 때, <heapify>라는 <Heap>의 연산을 $O(\log N)$의 시간으로 효율적으로 수행할 수 있기 때문에 <Heap>의 구현으로 자주 소개된다. 물론 이런 배열로 구현하지 않고, 평범한 트리 형태로 구현해도 동일한 효율을 보인다.

Heap-Order.
부모 노드의 키가 자식 노드의 키보다 항상 크거나 같다.

<Binary Heap>에서의 $\texttt{insert}$와 $\texttt{deleteMin}$는 루트 노드에서 말단 노드까지 또는 그 반대 방향으로 $\texttt{swim}$ & $\texttt{sink}$ 연산을 수행하는 것으로 이루어진다.

$\texttt{swim}$은 부모 노드보다 큰 key를 가진 자식 노드가 부모 노드와 swap 되어 루트 노드 쪽으로 올라가는 것을 말한다.

$\texttt{sink}$는 자식 노드보다 작은 key를 가진 부모 노드가 자식 노드와 swap 되어 말단 노드 쪽으로 내려가는 것을 말한다.

이번 포스트에서 <Binary Heap>에 대해 간단히 소개만 하고, 동작과 구현을 자세히 논하지는 않겠다. 추후에 <Binary Heap>의 구현 코드에서 좀더 자세히 다루고, 지금은 Time Complexity 위주로 살펴보겠다.

• $\texttt{getMin}$: $O(1)$
  • 루트 노드를 리턴
• $\texttt{insert}$: $O(\log N)$
  • 최악의 경우, <Heap>의 깊이 만큼 $\texttt{swim}$ 연산을 수행.
  • Complete Binary Tree이기 때문에 깊이 $D$는 $O(\log N)$이다 → $O(\log N)$
• $\texttt{deleteMin}$: $O(\log N)$
  • 맨 뒤 원소를 루트로 swap 후, 루트 노드 였던 것을 삭제
  • 최악의 경우, <Heap>의 깊이 만큼 루트 노드에서부터 $\texttt{sink}$ 연산을 수행 → $O(\log N)$

---

d-ary Heap

<d-ary Heap>은 <Binary Heap>의 generalization이다. <Binary Heap>은 각 노드가 2개의 자식 노드를 가졌다면, <d-ary Heap>은 각 노드가 d개의 자식 노드를 가지는 Complete Tree이다. 따라서, <Binary Heap>은 $d=2$인 특수한 경우라고 볼 수 있다.

<d-ary Heap>의 동작은 <Binary Heap>의 동작과 동일하다. 각 노드는 Heap Order를 만족해야 하며, Heapify를 통해 Heap을 구성한다. 다만, 자식 노드의 수가 많아져, Heap의 깊이 $D$가 $\log_d N$으로 얕아 졌다. 이에 따라 각 연산의 Time Complexity는 아래와 같이 유도된다.

• $\texttt{getMin}$: $O(1)$
  • 루트 노드를 리턴
• $\texttt{insert}$: $O(\log_d N)$
• $\texttt{deleteMin}$: $O(d \log_d N)$

* $\texttt{deleteMin}$ in d-ary Heap

먼저 $d=2$인 Binary Heap의 경우를 살펴보자. 만약 현재 min-Heap이 아래와 같이 구성되어 있다면,

   3       2       1
  / \  →  / \  →  / \
  2 1     3 1     3 2

와 같은 방식으로 최대 2번 $\texttt{Heapify}$를 호출한다.

이번에는 $d=3$인 경우를 살펴보자. 만약 현재 min-Heap이 아래와 같이 구성되어 있다면,

    4         3         2         1
  / | \  →  / | \  →  / | \  →  / | \
 3  2  1   4  2  1   4  3  1   4  3  2

와 같은 방식으로 최대 3번의 $\texttt{Heapify}$를 호출한다.

각 $\texttt{Heapify}$는 $O(\log_d N)$의 시간이 소요되므로, $\texttt{deleteMin}$은 $O(d \log_d N)$의 시간이 소요된다.

ps) $d=3$인 d-ary Heap을 <Ternary Heap>이라고도 부른다.

💥 Wikipedia에 기술된 내용에 따르면, 실전에서는 <4-ary Heap>이 $\texttt{deleteMin}$ 시간복잡도에서 열세임에도 불구하고, <Binary Heap> 보다 더 좋은 성능을 낸다고 한다. 그 이유는 <4-ary Heap>이 <Binary Heap>보다 Cache에서 더 이득을 보기 때문이라고 한다 😁

---

Binomial Heap

<Binomial Heap>은 서로 다른 두 Heap을 병합(merge)해 새로운 Heap을 구성하는 것에 특화된 Heap 구조다.

<Binomial Heap>은 <Binomial Tree>라는 특별한 형태의 트리의 집합으로 구성된다. 먼저 <Binomial Tree>에 대해 살펴본 후, <Binomial Heap>에 대해 살펴보겠다. 이번 포스트의 내용은 아래 유튜브 영상의 내용을 적절히 정리한 것임을 미리 밝힌다.

Binomial Tree

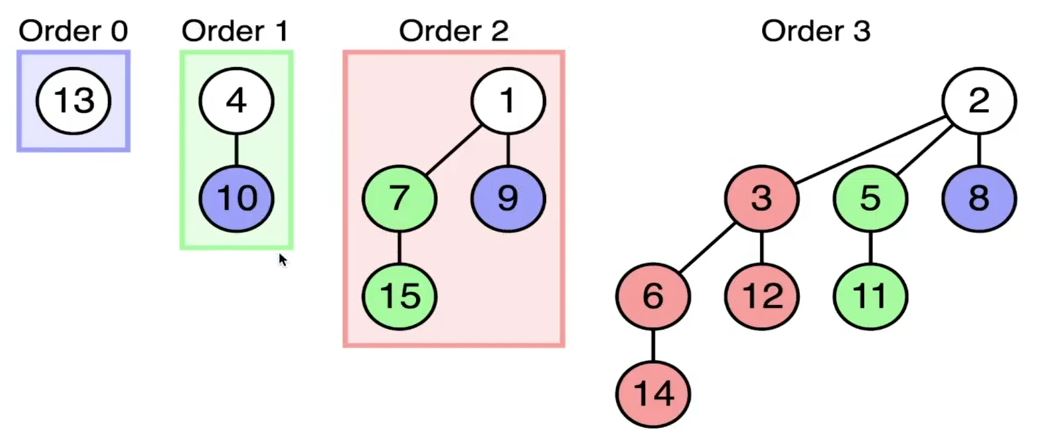
<Binomial Tree>는 degree가 같은 두 <Binomial Tree>를 병합(merge)함으로써 구축한다. 방법은 그렇게 어렵지 않고, 아래의 예시를 보면 바로 이해 될 것이다. 😊

(deg 0)   (deg 0)       (deg 1)       |    (deg 1)   (deg 1)       (deg 2)
   4    +    10     →       4         |       1    +    7     →       1
                            |         |       |         |           / |
                            10        |       9         15         7  9
                                      |                            |
                                      |                           15

<Binomial Tree>는 아래의 4가지 성질을 만족한다.

1. degree $k$의 <Binomial Tree>의 루트 노드는 정확히 $k$개의 자식 노드를 갖는다.

2. degree $k$의 <Binomial Tree>는 정확히 $2^k$개의 노드와 깊이 $k$를 갖는다.

3. <Binomial Tree>의 루트 노드는 degree $k-1$, $k-2$, …, $0$의 Binomial Tree를 자식으로 갖는다.

4. degree $k$의 <Binomial Tree>에서 depth $d$를 갖는 노드의 수는 $\displaystyle\binom{k}{d}$이다. 이 성질 때문에 <Binomial Tree>라는 이름이 붙었다 😎

Binomial Heap

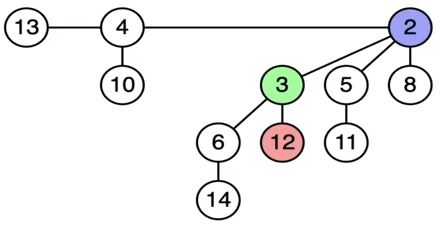
다시 <Binomial Heap>으로 돌아오자. <Binomial Heap>은 아래의 조건에 따라 모인 <Binomial Tree>의 집합이다.

1. Heap을 구성하는 각 Binomial Tree는 Heap Order를 따른다.

2. degree 0을 포함해 각 order별로 0개 또는 1개, 즉 각 order별 최대 1개의 이항 트리가 Heap에 존재한다.

2번재 조건은 전체 $n$개 노드가 존재할 때, <Binomial Heap>이 최대 $(1 + \log n)$개의 이항 트리로 구성됨을 말한다. 그 이유는 degree $k$인 Binomial Tree가 $2^k$ 만큼의 노드를 가지기 때문이다! 또한, Heap에 존재하는 각 Binomial Tree의 degree는 유일하게 결정된다. 전체 노드의 수 $n$을 이진수로 표현한다면, 각 digit은 Heap에 존재하는 Binomial Tree의 갯수를 의미한다. 따라서, 전체 노드 수 $n$에 대해 Binomial Heap의 구성은 유일하다! 💥

Merge.

Binomial Heap은 $\texttt{Merge}$라는 연산이 추가되었다. 일반적인 Heap과 달리 빠른 Merge를 지원한다는 게 장점이다.

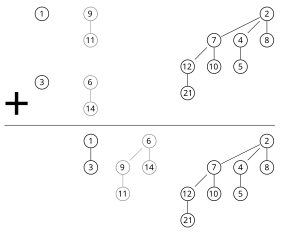
Image from Wikipedia

위와 같이 두 Binomial Heap을 병합하는 경우를 살펴보자. 이때, 두 Heap의 노드 수가 $N$, $M$이라면, 두 Heap에 존재하는 Tree의 수는 $1 + \log N$, $1 + \log M$이 된다.

이때, 두 Binomial Heap을 병합하는 것은 같은 degree를 갖는 Binomial Tree를 병합하는 것 같다. 이 Tree 병합 연산은 $O(1)$에 수행되고, 또 이 과정이 최대 Tree의 갯수 만큼 필요하므로 총 $O(\log N + \log M)$ 만큼의 Time Complexity를 갖는다.

앞에서도 언급했듯 Binomial Heap은 그 구성에 따라 이진수로 인코딩 될 수 있는데, Heap Merge 과정을 아래와 같이 이진수 덧셈의 관점에서 해석할 수도 있다. $N$-자릿수 이진수와 $M$-자릿수 이진수의 덧셈은 $O(N + M)$의 Time Complexity를 갖는 걸 생각하면, 두 과정이 정말 유사함을 깨달을 수 있다 🤩

Insert.

Binomial Heap에 새로운 원소를 추가하는 것은 단순히 degree 0의 Binomial Tree를 추가하는 것과 같다. 그래서 앞에서 언급한 $\texttt{merge}$의 상황과 비슷하게 동작한다. 따라서, Time Complexity는 $O(\log N)$이다.

getMin.

Binomial Heap을 이루는 Tree의 루트 노드를 살펴보면 된다. 따라서, Time Complexity는 $O(\log N)$. 만약 Heap에 Min-elt를 가리키는 포인터가 존재한다면, $O(1)$의 시간이 걸린다. 보통은 $O(1)$로 구현한다 😉

deleteMin.

먼저 $\texttt{getMin}$으로 루트 노드를 삭제할 Binomial Tree를 특정한다. Tree의 루트 노드를 제거하면, 해당 Tree의 자식 트리들이 남게 된다. 만약 $k$번째 binomial tree의 루트 노드를 제거했다면, $k$개의 children binomial tree를 얻게 된다. 새로 생긴 $k$개의 Children Binomial Tree들을 바탕으로 다시 $\texttt{merge}$ 연산을 수행한다. 이때, BIN Heap에 존재하는 $1 + \log N$개의 트리 중 마지막 번째 트리의 루트노드가 제거되었다면, $log N$ 만큼의 binomial tree 또는 $\log N$ 만큼의 binomial tree를 갖는 BIN heap이 새로 생긴다. 기존의 BIN heap과 새로 생긴 BIN heap을 merge 하면, Time Complexity는 $O(\log N + \log N) = O(\log N)$이다.

Image from Wikipedia

일반적으로 Binomial Heap은 Linked List로 구현한다. 이때, 일반적인 형태의 Linked List Tree에서 sibling 요소를 추가로 저장해 관리한다. <Binomial Heap>의 구현에 대한 자세한 내용은 추후에 별도의 포스트에서 다루도록 하겠다 😎

---

Lazy-Binomial Heap

이번 포스트의 내용은 아래 유튜브 영상의 내용을 적절히 정리한 것임을 미리 밝힌다.

<Lazy-Binomial Heap>은 앞에서 살펴본 <Binomial Heap>과 마찬가지로 Heap의 $\texttt{merge}$ 연산에 특화된 자료 구조다! 전체적인 개념은 <Binomial Heap>과 유사하고, $\texttt{marge}$와 $\texttt{extractMin}$ 연산에서 차이가 있다.

일단 <Lazy-Binomial Heap>의 아이디어는 “merge lazily!”이다. <Lazy-Binomial Heap>의 $\texttt{merge}$ 연산은 그냥 두 BIN Heap을 concatenate로 붙이는 것에 불과하다. 그래서 $O(\log n + \log m)$의 비용이 드는 <BIN Heap>과 달리, <Lazy-BIN Heap>에서는 $O(1)$의 비용이 든다! 😲 마찬가지로 원소를 하나 추가하는 $\texttt{insert}$ 연산 역시 $O(1)$의 비용이 든다.

하지만, 위와 같이 $\texttt{merge}$를 수행할 경우, 앞에서 살펴본 <BIN Heap>의 아름답고 좋은 성질이 깨지게 된다 😥 <Lazy-BIN Heap>에서는 BIN Tree의 degree는 규칙성 없이 자유롭게 분포되어 있을 것이다.

이번에는 <Lazy-BIN Heap>의 $\texttt{extractMin}$ 연산을 살펴보자. 이 연산은 Heap에서 가장 작은 원소를 제거한다. <Lazy-BIN Heap>은 이 $\texttt{extractMin}$ 연산이 수행될 때, $\texttt{consolidation}$(= 합병, 병합)을 수행하여 <Lazy-BIN Heap>에서 BIN Heap의 구조를 다시 구축한다.

이 $\texttt{consolidation}$이 수행되는 과정의 시간 복잡도를 분석해보자. degree가 자유롭게 분포되어 있는 상황에서 $\texttt{consolidation}$을 수행하는 방법을 각 BIN Tree를 degree 별로 정렬하여 앞에서부터 차례로 Tree를 합치는 것이다. 원래는 정렬을 수행할 때, $O(t \log t)$ ($t$는 Heap에 존재하는 BIN Tree의 수) 만큼의 시간이 소요된다. 그런데 정렬 과정에서 <Bucket Sort>를 사용한다면, BIN Tree 탐색에 $O(t)$, Bucket의 수 $O(\log n)$ 만큼 BIN tree merge 비용이 들어 $O(t + \log n)$의 비용으로 $\texttt{consolidation}$을 수행할 수 있다. 자세한 내용은 아래의 영상을 참고하자!

👉 Jeff Zhang - Lazy Binomial Heap Intro Part 1 of 2

$\texttt{extractMin}$ 연산에 대해서는 그 시간 복잡도가 “amortized $O(\log n)$”라고 한다. 시간 복잡도 분석에 <Potential Method>를 사용하는데, Potential Method에 소개하는 lecture note Lecture 20: Amortized Analysis와 Lazy-BIN Heap을 Potential Method로 분석한 이 lecture note Lecture 3: Fibonacci Heaps를 잘 읽어보면 그럭저럭 이해할 수 있다 🤞

Operation	Binomial Heap	Lazy-Binomial Heap
$\texttt{insert}$	$O(\log n)$	$O(1)$
$\texttt{getMin}$	$O(1)$	$O(1)$
$\texttt{extractMin}$	$O(\log n)$	amortized $O(\log n)$
$\texttt{merge}$	$O(\log n)$	$O(1)$

---

Fibonacci Heap

이번 포스트의 내용은 아래 유튜브 영상의 내용을 적절히 정리한 것임을 미리 밝힌다.

마지막으로 다룰 Heap 구조는 <Fibonacci Heap>이다 😎 개인적으로 마지막에 유도되는 만큼 가장 어려운 Heap 구조라고 생각한다 😱

먼저 <Fibonacci Heap>은 앞에서 다룬 <Lazy-Binomial Heap>보다 더 Lazy 한 녀석이다! <Lazy-BIN Heap>보다 $\texttt{decreaseKey}$ 연산을 Lazy 하게 처리해서 비용을 더 줄인다!

사실 “Lazy decreaseKey” 연산의 아이디어 자체는 간단하다. $\texttt{decreaseKey}$를 수행할 때, heap-order를 벗어나는 부분에 대해서는 잘라낸다는 게 전부다.

<BIN Heap>에서 $\texttt{decreaseKey}$ 연산을 수행하면 $\texttt{Heapify}$ 때문에 트리의 높이 만큼, 즉 $O(\log n)$의 비용이 들었다. 그러나 <Fibonacci Heap>은 대상이 되는 BIN tree를 잘라내기 때문에 $\texttt{Heapify}$ 연산 없이 $O(1)$의 비용만 든다.

여기서 잠깐 지금까지 <BIN Heap>에서 개선된 부분들을 짚고 넘어가자.

• Merge: $O(\log n + \log m) \rightarrow O(1)$ (by Lazy-BIN Heap)
• Insert: $O(\log n) \rightarrow O(1)$ (by Lazy-BIN Heap)
• extractMin: $O(\log n) \rightarrow \text{amoritzed} \; O(\log n)$ (by Lazy-BIN Heap)
• deleteKey: $O(\log n) \rightarrow O(1)$ (by Fibonacci Heap!) 🔥

위 연산들에 대한 비용이 줄었지만, 또 위 연산들이 Heap 구조를 엉망으로 만드는 주범이기도 하다 🤦‍♂️ 그리고 Fibo Heap의 변화된 $\texttt{deleteKey}$ 연산은 $\texttt{extractMin}$ 연산의 성능에 영향을 끼친다 😱

그.러.나. 안심하라! Lazy decreaseKey를 도입하더라도 $\texttt{extractMin}$의 비용은 여전히 “amortized $O(\log n)$”이다! 😲

<Fibonacci Heap>에서 수행되는 $\texttt{extractMin}$을 좀더 살펴보자. $\texttt{extractMin}$ 이후 수행되는 $\texttt{consolidate}$ 연산은 Heap을 이루는 트리를 degree $k$에 따라 “Bucket Sort”로 정렬하여 차례로 새로운 트리를 만든다.

하지만, Lazy decreaseKey 연산을 수행하면 더이상 Heap에 존재하는 Tree는 BIN Tree의 조건을 만족하지 않게 된다. 왜냐하면, BIN Tree가 되려면 degree $k$일 때, $2^k$ 개의 노드가 있어야 하기 때문이다. (Fibo Heap에서는 $2^k$ 보다 적은 수의 노드가 트리에 남게 된다.)

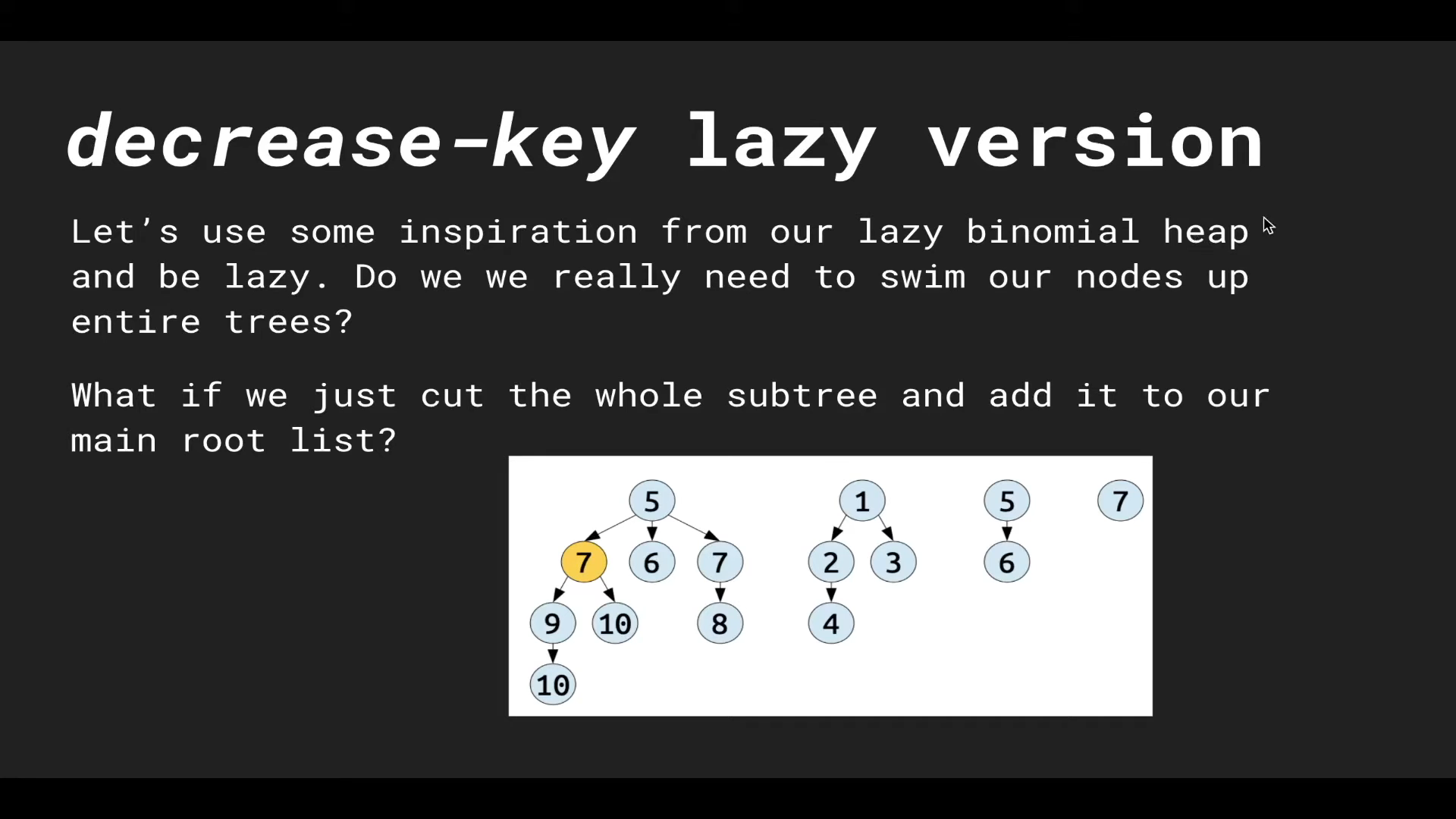
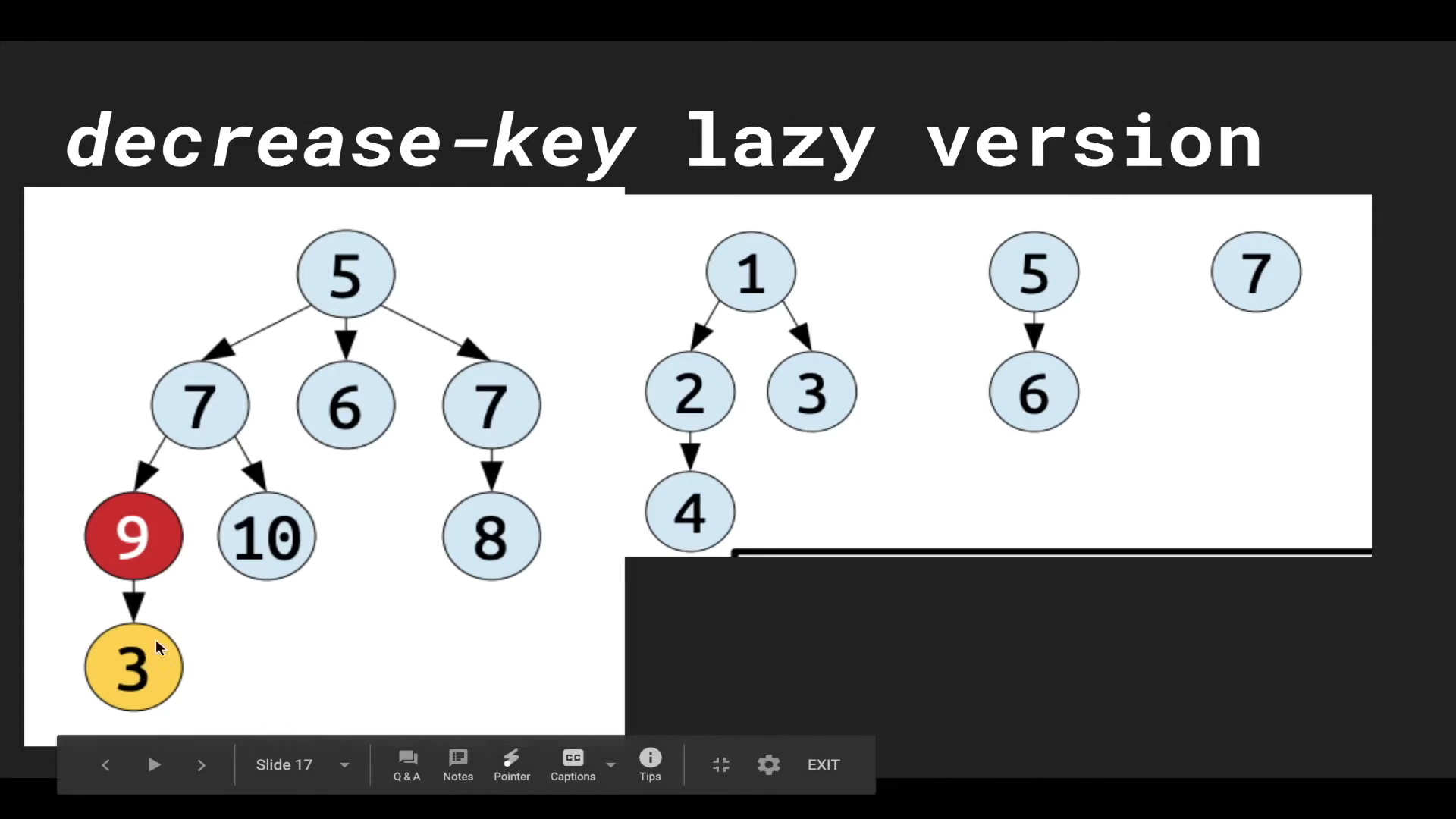
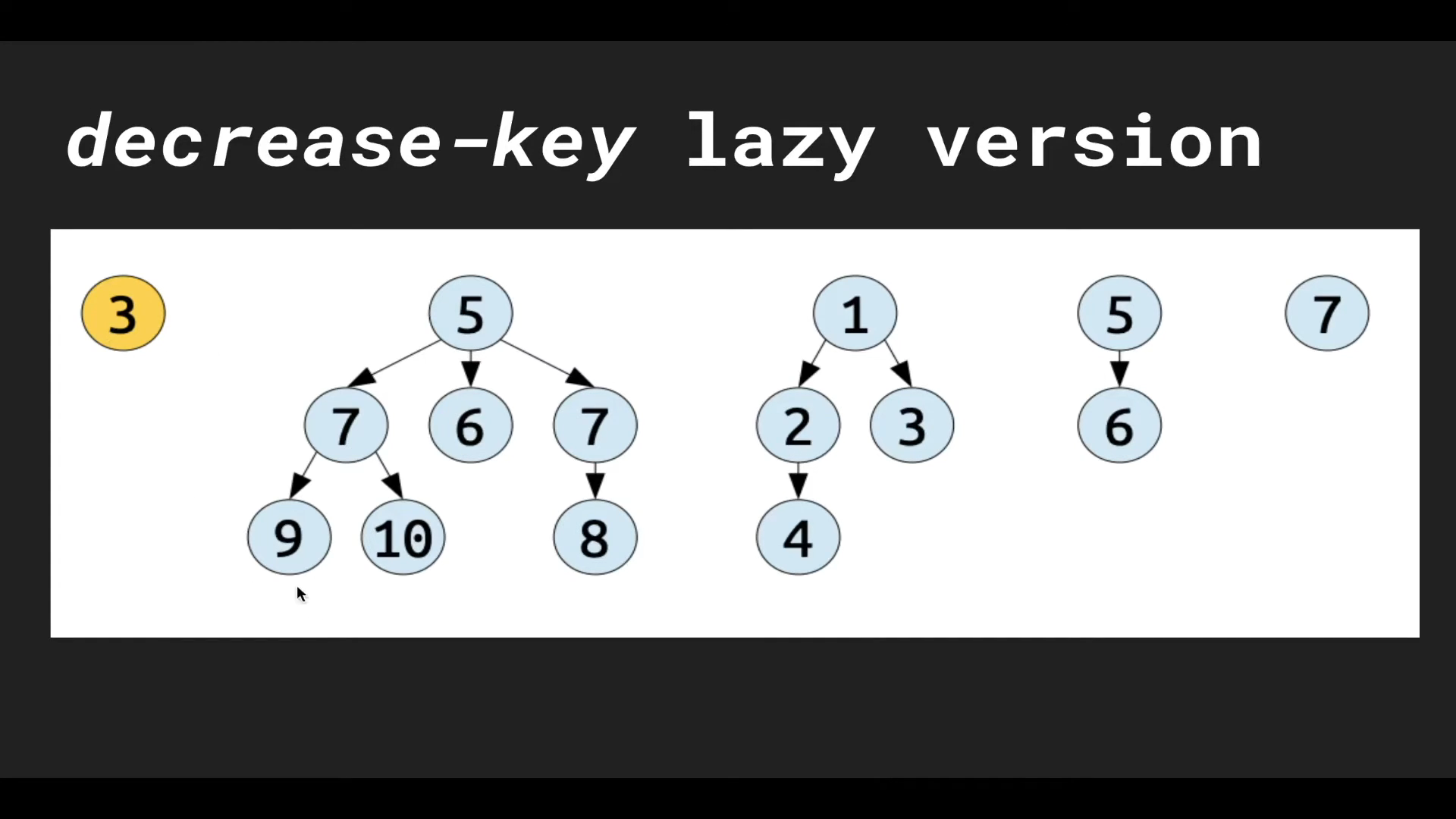
예를 들어 왼쪽의 BIN tree에서 ‘10’의 키를 가진 말단 노드의 키를 ‘3’으로 바꾼다면, 그 노드를 BIN tree에서 분리(cut)하는 방식으로 $\texttt{decreaseKey}$ 연산을 수행한다. 이것은 $\texttt{decreaseKey}$ 연산의 대상이 되는 BIN tree가 더이상 BIN tree의 성질을 만족하지 못 하도록 만든다.

이런 문제 때문에 트리를 degree $k$로 분류하는 것이 불가능 해 $\texttt{consolidate}$ 단계에서 Bucket Sort를 수행할 수 없다 😱 그래서 <Fibonacci Heap>에서는 트리의 degree를 아래와 같이 새롭게 정의하여 사용한다.

A tree has degree $k$, if its root has $k$ children.

Fibo Heap에서는 위의 정의를 사용해 Bucket Sort를 수행하며, 엉망이 된 BIN Heap을 정리(clean-up)한다. 그러나…

그러나! 위와 같이 $\texttt{decreaseKey}$와 $\texttt{consolidate}$를 수행하게 되면, 최악의 경우에는 $\texttt{decreaseKey}$에 의해 Heap이 degree 0의 트리 $n$개로 이뤄진 후에 $\texttt{consolidate}$가 이뤄질 수 있다 🤦‍♂️ 이 경우, 비용은 $O(n)$이다…

BIN tree를 기반으로 하는 <BIN Heap>과 <Lazy-BIN Heap>은 트리의 사이즈가 $2^k$로 exponential 하게 증가해서 $\text{amortized} \; O(\log n)$로 $\texttt{consolidate}$ 연산이 가능했다.

위의 문제를 해결하기 위해, Fibo Heap에서는 $\texttt{decreaseKey}$ 연산에 새로운 규칙을 추가한다.

Paraents can lose at most one children.

If a parent loses two children, we also cut the parent off from the grand-parent.

위 규칙은 Heap을 엉성하게나마 “logarithmic”하도록 만든다. 이것에 대한 구현은 생각보다 간단하다. 그냥 부모 노드가 $\texttt{decreaseKey}$에 의해 자식 노드를 잃으면 그 부모 노드를 “마킹” 해둔다. 이후에 부모 노드가 또 한번 자식 노드를 잃는다면, 그때는 부모 노드를 조부모 노드로부터 분리시킨다! // 영상에서 잘 설명하니 이 부분은 영상을 보자!

글로는 감이 안 잡히니, 그림으로 살펴보자!

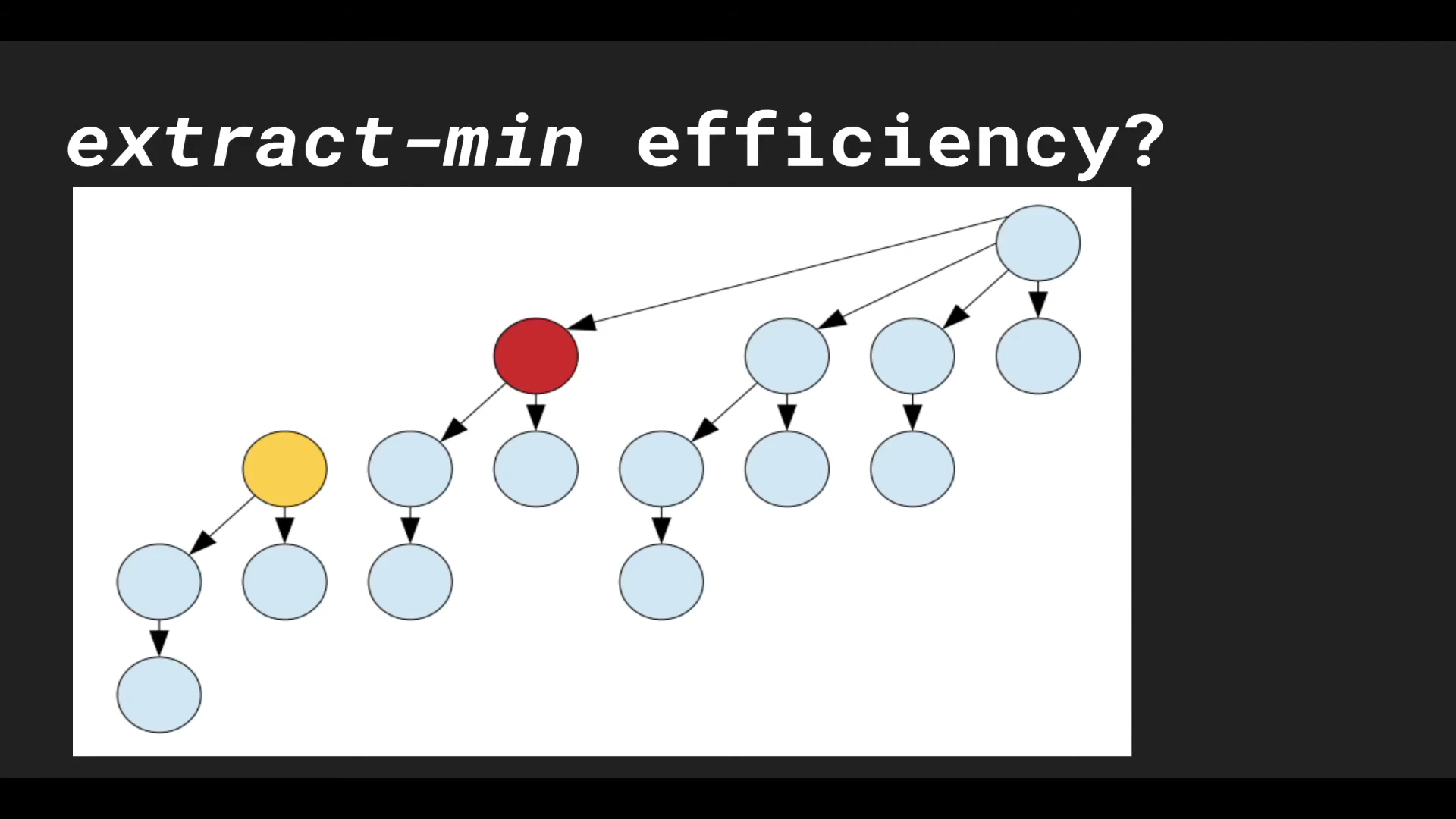
BIN tree가 child를 하나 잃어 붉은색으로 마킹 되었다.

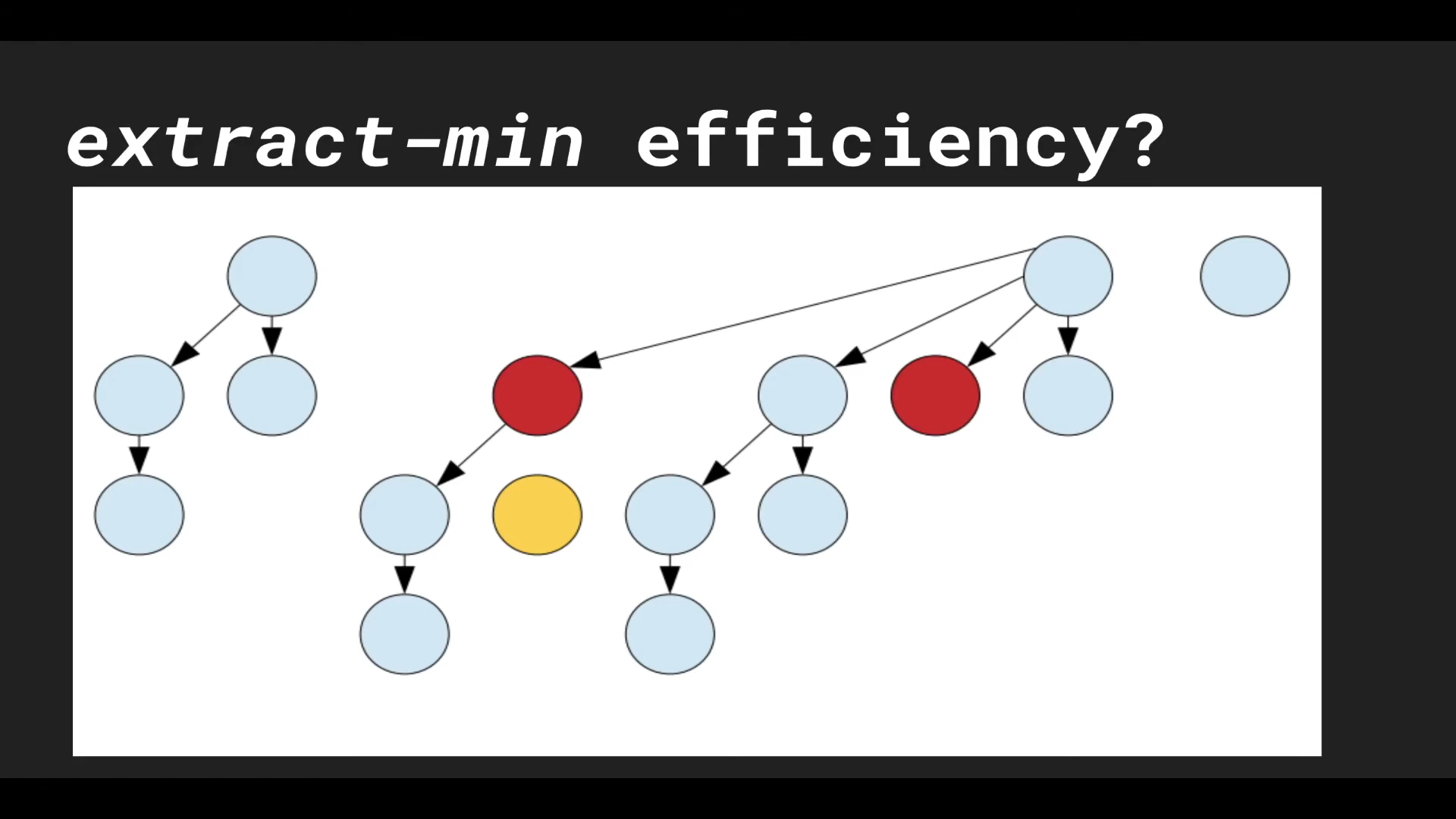
붉은색으로 마킹된 노드가 또 하나의 자식 노드를 잃었다!

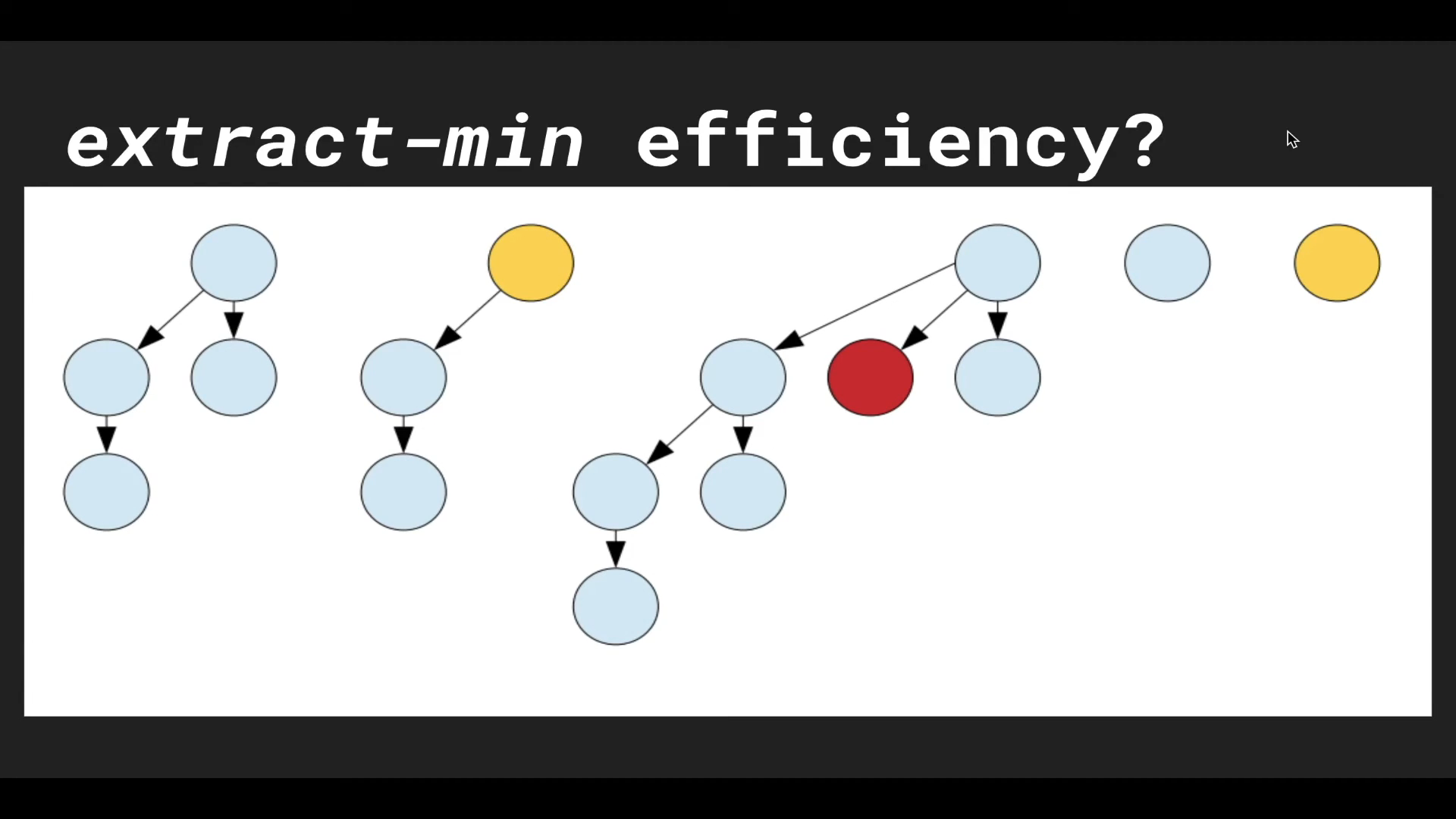
그러면 해당 노드를 부모 노드로부터 분리시킨다!

추가된 규칙은 BIN Heap의 “root list”의 크기를 approximately logarithmic 하게 유지해준다고 한다. 그래서 <Fibonacci Heap>의 $\texttt{extractMin}$도 $\text{amortized} \; O(\log n)$의 시간으로 수행된다! 😁 자세한 내용은 Lecture 3: Fibonacci Heaps의 “5. Analysis”를 통해 확인할 수 있다.

이 정도면 충분할 것 같은데, <Fibonacci Heap>은 여기서 <Maximally Damaged Tree>라는 개념을 또 소개한다! 😱 이 녀석에 의해 이 Heap 구조가 “Fibonacci” Heap이라고 불리게 되었으니 조금만 더 힘을 내보자! 🤦‍♂️ (시간복잡도와 관련된 개념은 아니니 가벼운 마음으로 읽자 😄)

A <maximally damaged tree> is a binomial tree of degree $k$¹ which has been maximally damaged by cutting off subtrees from the lazy decreaseKey operation.

<Maximally damaged tree>란 degree $k$의 BIN Tree에 $\texttt{decreaseKey}$를 수행할 때, Tree의 degree $k$를 훼손하지 않을때까지 $\texttt{decreaseKey}$를 수행한 트리를 말한다. 이 개념은 우리가 앞에서 정의한 새로운 $\texttt{decreaseKey}$의 방식에서 자연스럽게 유도되는 개념이다. // 이 부분 역시 영상에서 잘 설명하니 영상을 보자!

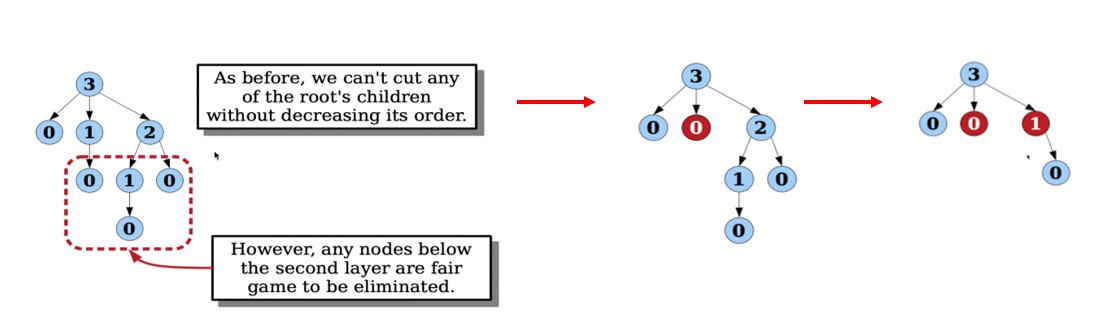
BIN tree의 degree가 줄지 않을 때까지 $\texttt{decreaseKey}$를 수행한 모습

Corollary.

A <maximally-damaged tree of degree $k$> is a tree whose children are maximally-damaged trees of degrees $0, 0, 1, 2, 3, \dots, k-2$.

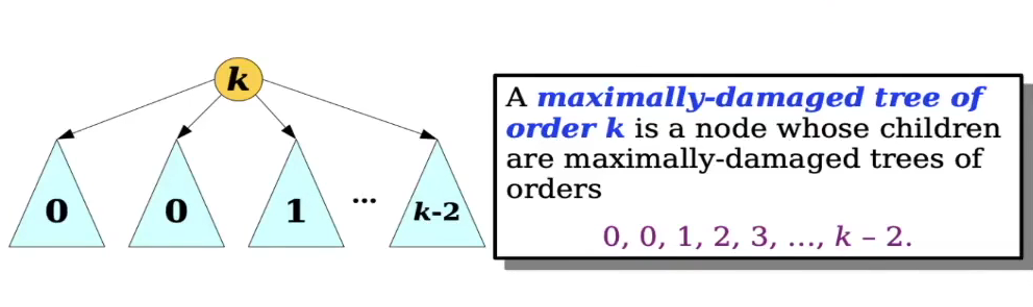
위의 따름 정리에 의해 <maximally damaged tree>에서는 아래의 정리가 성립한다! 😲

Theorem.

The #. of nodes in a <maximally damaged tree of degree $k$> is $F_{k+2}$.

증명은 위의 따름 정리의 사실을 그대로 수식으로 기술하면 된다. 😉

지금까지 살펴본 <BIN Heap>과 그 변형들에 대한 연산의 시간복잡도를 정리하면 아래와 같다 🙌

Operation	Binomial Heap	Lazy-Binomial Heap	Fibonacci Heap
$\texttt{insert}$	$O(\log n)$	$O(1)$	$O(1)$
$\texttt{getMin}$	$O(1)$	$O(1)$	$O(1)$
$\texttt{extractMin}$	$O(\log n)$	amortized $O(\log n)$	amortized $O(\log n)$
$\texttt{merge}$	$O(\log n)$	$O(1)$	$O(1)$
$\texttt{decreaseKey}$	$O(\log n)$	$O(\log n)$	$O(1)$

---

지금까지 <Heap> 또는 <Priority Queue>의 주요한 구조들을 살펴봤다. 솔직히 말해 실전에서 자주 쓰는 구조들은 아니지만, <알고리즘> 수업과 자료들에서 종종 등장해서 이번 기회에 쭉 정리해보았다.

<Heap>의 변형들이 뭐가 중요한가 싶지만 <Fibo Heap>이 소개된 아티클에 따르면 <Fibo Heap>을 도입함으로써 Dijkstra’s single-source shortest path algorithm의 성능이 $O(E \log E)$에서 $O(E + V \log V)$로 획기적으로 줄었다고 한다! 😲

---

참고자료

• ‘핑크마구로’님의 포스트
  • PQ에 대한 문제와 PQ를 이용한 <A* Algorithm> 등 다양한 내용의 포스트가 있습니다 👍
• geeksforgeeks: K-ary Heap
• Wikipedia: d-ary heap
• Wikipedia: Binomial heap
• ‘Jeff Zhang’의 유튜브 영상 - Binomial Heap
• ‘Jeff Zhang’의 유튜브 영상 - Lazy-Binomial Heap
• ‘Jeff Zhang’의 유튜브 영상 - Fibonacci Heap
• Lecture 20: Amortized Analysis
• Lecture 03: Fibonacci Heaps

---

1. 이때 degree의 의미는 <Fibonacci Heap>에서 새롭게 도입한, children의 갯수의 $k$다. ↩