Asymptotic Analysis
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
보통 우리는 어떤 알고리즘의 성능을 입력 데이터의 크기 $N$에 대한 함수로 표현한다. 이번 포스트에서는 알고리즘의 성능을 표기하는 여러 기법들에 대해 살펴본다 😎
$O$ Notaiton
For two functions $f(n)$ and $g(n)$, $f(n) = O(g(n))$,
iff there exist a constant $c > 0$ and $n_0 \ge 0$ s.t. for all $n \ge n_0$,
we have $f(n) \le c\cdot g(n)$
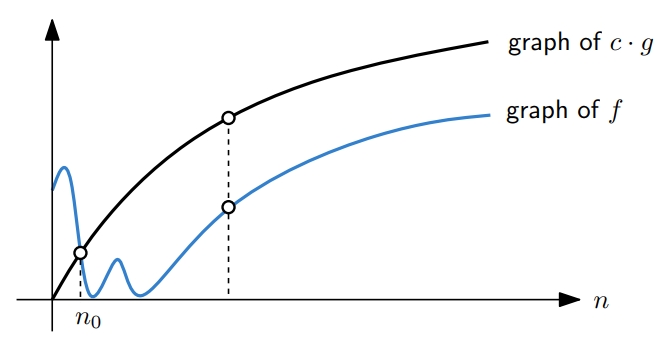
즉, $g(n)$ is an asymptotic upper bound of $f(n)$.
$\Omega$ Notaiton
For two functions $f(n)$ and $g(n)$, $f(n) = \Omega(g(n))$,
iff there exist a constant $c > 0$ and $n_0 \ge 0$ s.t. for all $n \ge n_0$,
we have $f(n) \ge c\cdot g(n)$
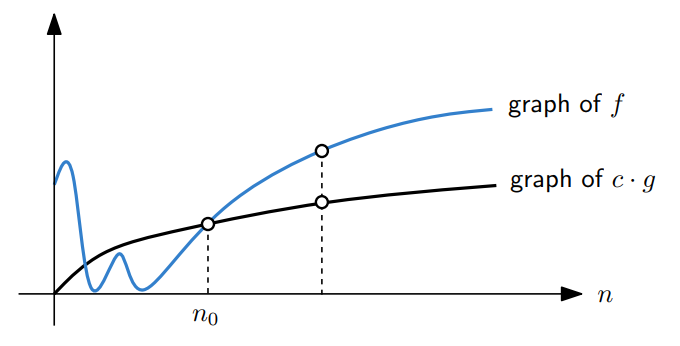
즉, $g(n)$ is an asymptotic lower bound of $f(n)$.
$\Theta$ Notaiton
$f(n)$ is $\Theta(g(n))$ iff $f(n) = \Omega(g(n)) = O(g(n))$.
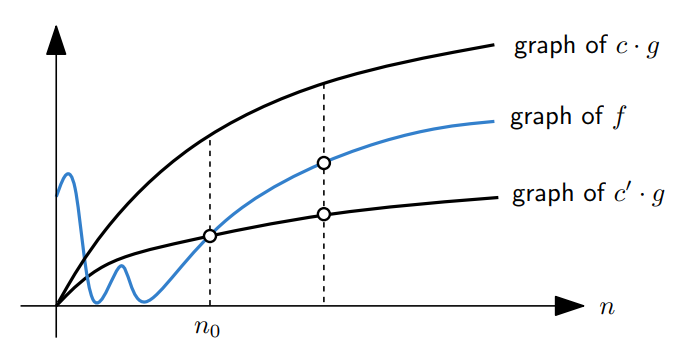
즉, $g(n)$ is an asymptotic approximation of $f(n)$.
Examples
표기법에 익숙해지기 위해 몇가지 문제를 풀어보자.
Q1. Show that for all positive integer $n$,
\[7n^5 + 1024 n^4 + 3n (\log n)^{248} + 10 = O(n^5)\]A1. 논리에 따라 조금만 끄적이면 금방 풀림.
Q2. (T/F) If $f(n) = \min \{ n, 10^6 \}$, then $O(1)$.
A2. E-Z
Q3. (T/F) If $f(n) = O(n)$, then $2^{f(n)} = O(2^n)$.
A3. E-Z
Other Asymptotic Bounds
Definition. little-o notation
For every $\epsilon > 0$,
there exists a constant $n_0$ s.t. $f(n) \le \epsilon \cdot g(n)$ for $n > n_0$,
then $f(n) = o(g(n))$.
Definition. little-omega notation
if $g(n) = o(f(n))$, then $f(n) = \omega(g(n))$.
Examples
이해를 돕기 위해 사례를 먼저 살펴보자.
[Trivial case]
- $f(n) \ne o(f(n))$
-
$f(n) \ne \omega(f(n))$
- if $f(n) = o(g(n))$, then $f(n) = O(g(n))$. However, the converse is not true.
[Definition by Limitation]
If $\displaystyle\lim_{n\rightarrow\infty} \frac{f(n)}{g(n)} = 0$, then $f(n) = o(g(n))$.
Q4. (T/F) If $f(n) = 2^n$ and $g(n) = n^c$ for $c \in \mathbb{N}$, then $g(n) = o(f(n))$.
A4. E-Z. 앞에서 언급한 극한으로 정의한 little-o notation을 쓰면 바로 풀린다.
Q5. Show that for any fixed but arbitrarily small real number $c > 0$,
\[n \log n = o(n^{1+c})\]A5. E-Z. 이것도 극한으로 정의한 버전을 쓰면 바로 풀림.
Exercises
Q. (T/F) $2^n = n^{\omega(1)}$.
A. E-Z. 식을 잘 정리한 후에, 극한으로 정의한 버전을 씀.
이번에 살펴본 <Asymptotic Analysis>는 알고리즘의 성능을 개략적으로 판단하는 지표다. 경우에 따라서는 알고리즘에 붙은 덧셈·곱셈의 상수텀 역시 중요하다.
그러나 <Asympototic Analysis>는 최악의 상황 아래서 알고리즘의 성능을 평가하기 때문에, 이것이 오히려 알고리즘의 실제 비용을 부풀리게 만들기도 한다. 이런 문제점을 개선한 것이 바로 <Amortized Analysis>이다. 고급 자료구조를 쓸때 <Amortized Analysis>가 자주 등장하기 때문에, 꼭 알아야 하는 기법 중 하나다.