Convex hull Algorithm
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Definition. Convex hull
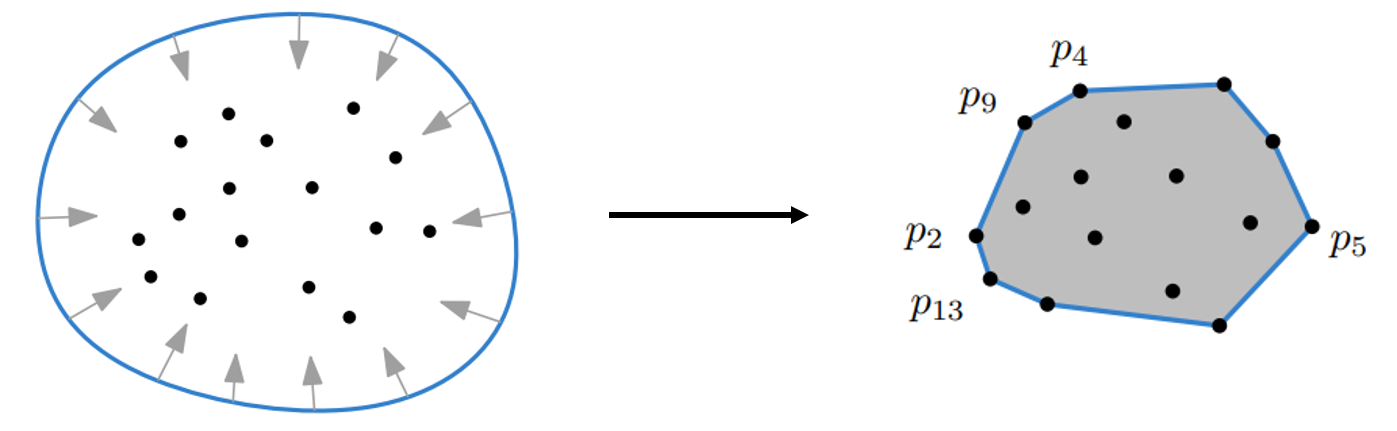
The <convex hull> of a set $P$ of points in the plane is the smallest convex set containing $P$.
Equivalently, it is the largest convex polygon whose vertices are points in $P$.
-
inputs: a set $P = \{ p_1, p_2, \dots, p_n \}$ of points, where $p_i = (x_i, y_i)$
-
output: $(p_2, p_9, \dots, p_5, \dots, p_13)$, a representation of the convex hull
💥 NOTE: We assume that the points in $P$ are in general position, meaning that no three points lie on a common line.
<Convex hull Algorithm>을 살펴보기 전에 먼저 아래의 문제를 풀어보자.
For three points $p$, $q$, $r$, how do we test whether $r$ lies to the left or to the right of the directed line $\vec{pq}$?
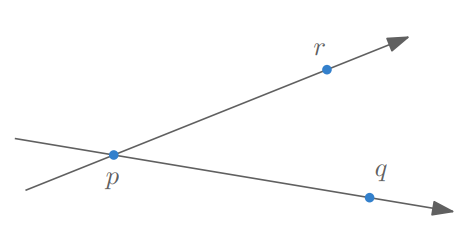
해결 방법은 의외로 간단하다!! 그냥 $\vec{pq}$를 지나는 직선과 $\vec{pr}$을 지나는 직선의 기울기를 비교해보면 된다!!
\[\frac{q_y - p_y}{q_x - p_x} \quad \text{vs.} \quad \frac{r_y - p_y}{r_x - p_x}\]이때, 식에 나눗셈이 있는 것은 “divide by zero”의 위험이 있기 때문에, 식을 곱셈의 형태로 바꿔준다.
\[(r_x - p_x) \cdot (q_y - p_y) \quad \text{vs.} \quad (q_x - p_x) \cdot (r_y - p_y)\]만약, 점 $r$이 직선 $\vec{pq}$의 왼쪽에 있다면, 위의 그림에서도 볼 수 있듯이, $\vec{pr}$의 기울기가 $\vec{pq}$ 보다 크게 된다. 따라서,
\[\frac{q_y - p_y}{q_x - p_x} \quad < \quad \frac{r_y - p_y}{r_x - p_x}\] \[(r_x - p_x) \cdot (q_y - p_y) \quad < \quad (q_x - p_x) \cdot (r_y - p_y)\]Brute Force
어떤 두 점 $p$, $q$가 convex hull을 이룬다고 생각해보자, 그러면 $\vec{pq}$에 대해 다른 모든 점들은 $\vec{pq}$의 오른편에 존재하게 된다.
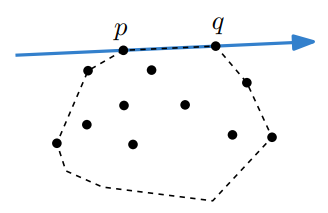
만약 이 과정을 naive 하게 진행한다면,
-
Pick two points from points set: $\displaystyle\binom{n}{2}$
-
Scan other points to determine they are in the right-side: $n$
그래서 시간 복잡도는 $O(n^3)$이 된다.
Graham’s Scan
$O(n^3)$ 수준의 알고리즘은 아직 많이 느리다. <Graham’s Scan>은 points를 정렬하고, 또 몇가지 규칙을 통해 $O(n^3)$보다 훨씬 빠른 알고리즘을 제시한다.
Algorithm.
// initialization
Sort points in $P$ by x-coord and y-coord: $O(n \log n)$
Let $p, q, r$ be the leftmost three points in the sorted list $L$.
Repeat this:
If $r$ lies to the right of $\vec{pq}$:
we move one step forward in $L$.
Otherwise:
remove $q$ from the sorted list and move one step backward in $L$ if possible.
글로 살펴보면 알고리즘의 행동이 잘 그려지지 않는다. 일단 용어를 조금 다듬으면,
- $r$는 우리가 살펴보는 직선 $\vec{pq}$의 바로 다음 정렬된 point
-
$q$는 우리의 직선 $\vec{pq}$의 끝점이다.
- “one step forward”라는 말은 $p$를 accept하고, 다음 정렬된 point로 넘어가라는 말이다.
// one step forward가 $r$을 accept 하는 것은 아니다. $r$은 언제든지 이후에 reject 될 수 있다! - “remove & one step backward”는 현재의 $\vec{pq}$에서 $q$를 reject하고, 마지막에 살펴본 2개 점으로 직선을 갱신
// 마찬가지로 이것은 $r$을 accept하는 것이 아니다!
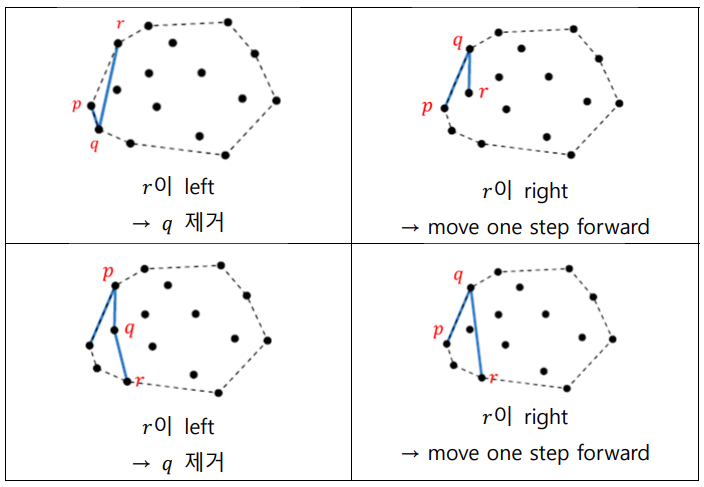
이 과정을 반복하면, sorted list $L$에 convex hull을 이루는 점들만 남게 된다!! 😎
<Graham’s Scan>의 시간 복잡도를 분석해보자. 각 과정의 반복 횟수 별로 생각해본다면,
- rule (1)만 계속 적용 → 최대 $n-2$번 적용 가능!
- 만약 sorted list $L$에 convex hull이 아닌 점들이 있다면, 우리는 rule (2)를 통해 그런 점들을 제거하게 된다. 따라서, rule (2)는 총 $n-h$번 적용된다! ($h$ = #. of upper convex hull points)
이렇게 <Graham’s Scran>을 하게 되면, 우리는 convex hull의 위 껍질을 얻게 된다!! 나머지 아래 껍질은 sorted list의 반대에서부터 rule을 뒤집어 적용하면 얻을 수 있다!!
알고리즘 테크닉 중에는 <Convex hull trick>라는 최적화 알고리즘이 있다. 사실 이름에 “Convex hull”이 붙었지만, <Convex hull algorithm>과는 전혀 다른 종류의 알고리즘이다.
추천 문제
- 백준 1708번: 볼록 껍질 // 좋은 문제다. 자료구조들에 대한 이해와 디테일을 신경써야 했다.
- 백준 4181번: Convex Hull
