Additive Model & GAM
2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Additive Model
Definition. Additive Model
The regression model
\[E (Y \mid X_1, \dots, X_p) = \alpha + f_1(X_1) + \cdots + f_p(X_p)\]is called an <additive model>.
It assumes that there is no interaction effect.
Therefore, it can effectively avoid “the curve of dimensionality”.
✨ Goal: How can we estimate $f_i(x_i)$?
이때 쓰는 접근법이 바로 <Backfitting Algorithm>이다.
보통 우리가 $f_j$를 제외한 나머지 $f_k$에 대한 함수를 알고 있을 때, $f_j$를 추정하는 것은 아주 쉽다. 그냥 1차원 문제를 해결하는 것이기 때문이다!
이렇게 다른 함수를 fix 시켜두고, 함수 하나를 fitting 하는 기법을 <Backfitting Algorithm>이라고 한다.’
Algorithm. Backfitting Algorithm
1. Initialize:
- $\hat{\alpha} = \bar{y}$
- for $\forall \, j$, $\hat{f}_j = 0$
2. Repeat until converge
find an estiamtor $\hat{f}_j$ based on \(\left\{ x_i, \; y_i - \hat{\alpha} - \displaystyle \sum_{k\ne j} \hat{f}_k(x_{ik}) \right\}^n_{i=1}\)
💥 이때, 2번째 스텝에서 <smoothing spline>이나 <kernel method> 등의 다른 non-parameteric method들을 적용해볼 수도 있다.
<Backfitting Algorithm>은 Convex optimization과 비슷하다고 하며, 굉장히 빠르게 수렴한다고 한다! 😲
GAM; Generalized Additive Model
<GAM; Generalized Additive Model>은 강력하면서도 간단한 통계적 테크닉 중 하나이다. 1986년, ESL의 공동저자인 “Trevor Hastie”와 “Robert Tibshirani”에 의해 개발된 방법이다.
Relationships btw the individual predictors and the dependent variable follow smooth patterns that can be linear or non-linear.
즉, GAM은 <Additive Model>에서 $f_j$가 smooth non-parametric인 모델이다!
‘DataCamp’의 유튜브 영상에서는 <GAM>이 <Linear Model>과 <Bloack-BOX ML> 모델의 중간 정도에 위치하는 모델이라고 소개한다.

Image from ‘DataCamp’
통계적 모델은 <Interpretability>와 <Flexibility>에 trade-off가 있는데, 왼편과 오른편이 각각을 의미한다.
<GAM>은 딱 중간 정도에 위치한 모델로, 적당한 <Interpretability>와 적당한 <Flexibility>를 제공한다.
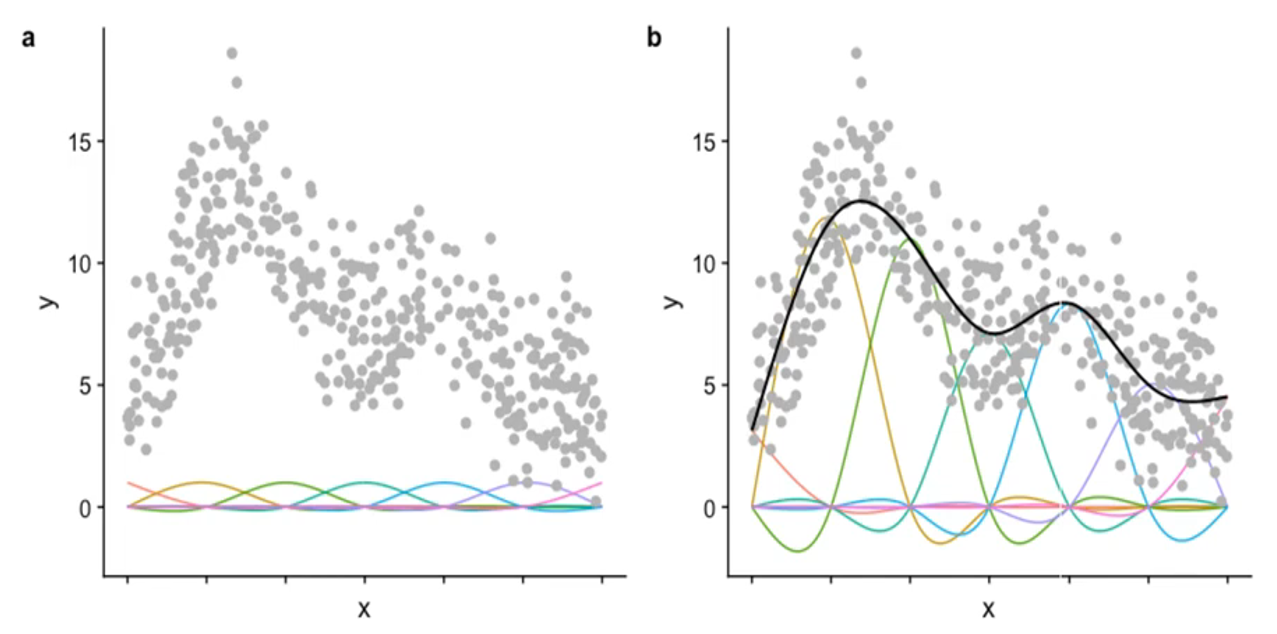
Image from ‘DataCamp’
위의 그림은 <GAM>에서 사용된 <smooth basis function>들을 표현한 것이다. 왼쪽 그림은 모든 basis func.에 동일한 coeff.를 준 그림이고, 오른쪽 그림은 학습을 통해 각 basis func.에 튜닝된 coeff.를 준 그림이다.
‘multithreaded’에 게시된 포스트에서는 GAM의 장점으로
(1) Interpretability
(2) Flexibility & Automation
(3) Regularization
을 꼽는다.
이 중에서 먼저 “Regularization“부터 살펴보자. smooth function을 추정하는 GAM은 “smoothness”를 컨트롤 하는 tuning parameter $\lambda$가 존재한다. 이것을 통해 overfitting을 방지하고, 전체 predictor가 wiggle 해지는 것을 방지한다.
‘DataCamp’의 유튜브 영상에 따르면, <GAM>은 아래의 수식에 따라 모델의 Wiggliness를 조정한다고 한다.
\[\text{Fit} = \text{Likelihood} - \lambda \times \text{Wiggliness}\]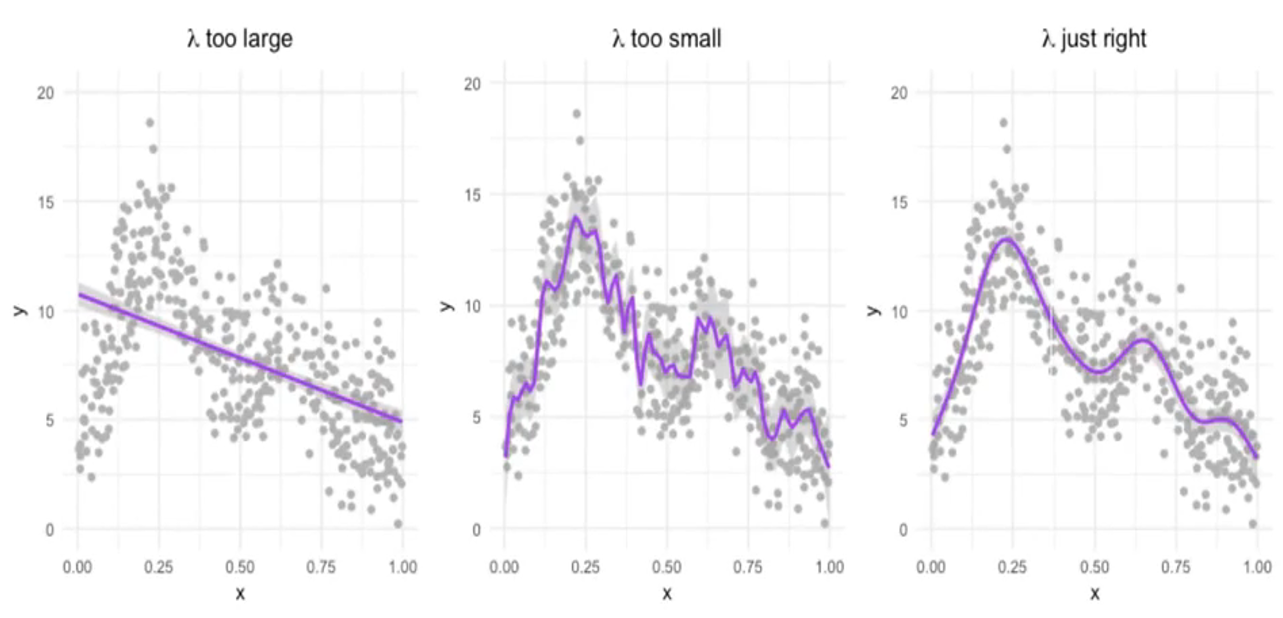
Image from ‘DataCamp’
또는 basis func.의 수로도 smoothness를 조정할 수 있다.
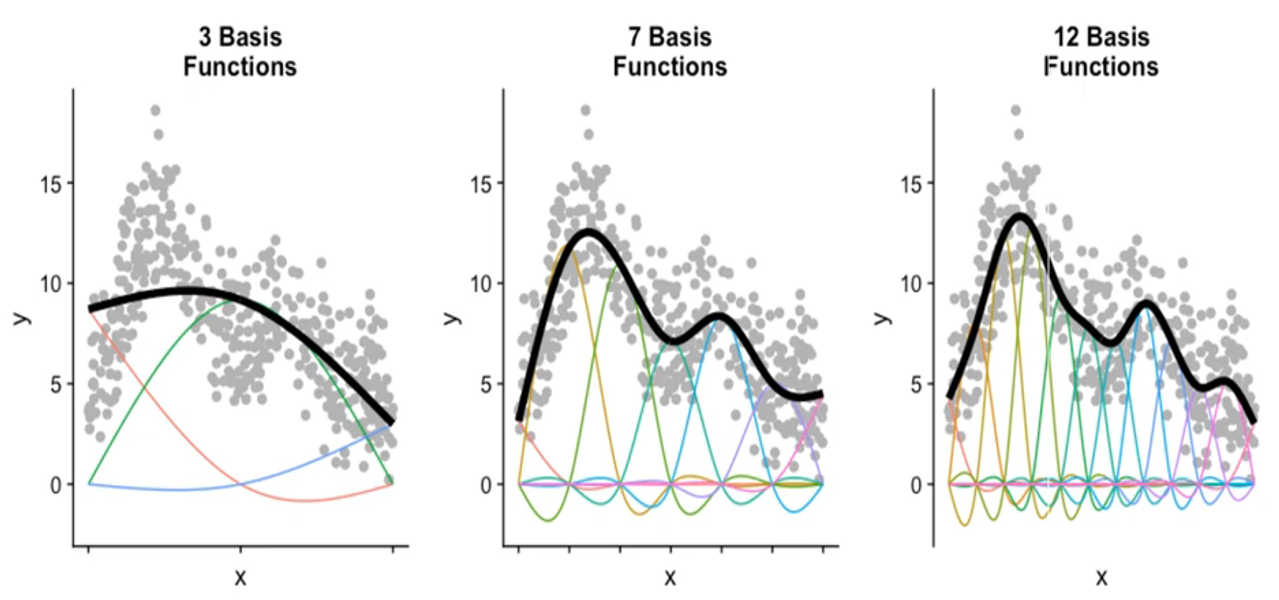
Image from ‘DataCamp’
<GAM>은 input feature 수가 여러 개일 때도 사용할 수 있다. 이때, 각 input feature가 independent 하다는 <additive model>의 가정을 사용한다!
자세한 내용은 ‘DataCamp’의 영상을 통해 살펴보자.
👉 [YouTube] R Tutorial: Multivariate GAMs
