Back-propagation
2020-1학기, 대학에서 ‘인공지능’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
Backpropagation
<Back-propagation>은 <GD>를 수행하기 위해 Loss의 편미분을 쉽게 구할 수 있게 하는 알고리즘이다.
\[\nabla_\mathbf{w} \text{TrainLoss}(\mathbf{w})\]<Back-propagation> 알고리즘은 <Neural Network>를 일종의 “Computational Graph“로 모델링 하여, Gradient를 구한다. Gradient는 <Chain Rule>에 의해 안쪽의 연산까지 차례대로 전파된다.
<Back-propagation>은 복잡한 형태의 Loss 함수일지라도 그것을 작은 요소부터 차례로 <Chain Rule>에 따라 Gradient을 구하기 때문에 복잡한 함수의 미분식을 직접 구하지 않고도 쉽게 Gradient를 구할 수 있다! 😁
Function as boxes
먼저 가장 간단한 형태의 <Computational Graph>부터 살펴보자.
Remark. basic building blocks
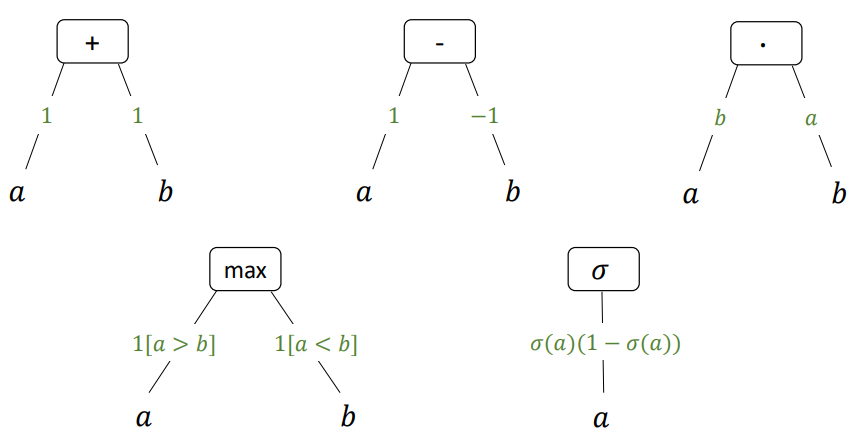
1. Addition $f(a, b) = a+b$
\[\frac{\partial f(a, b)}{\partial a} = 1 \quad, \quad \frac{\partial f(a, b)}{\partial b} = 1\]2. Multiplication $f(a, b) = ab$
\[\frac{\partial f(a, b)}{\partial a} = b \quad , \quad \frac{\partial f(a, b)}{\partial b} = a\]$a$, $b$의 순서가 바뀌었다!!
3. max function $f(a, b) = \max(a, b)$
\[\frac{\partial f(a, b)}{\partial a} = I[a > b] \quad , \quad \frac{\partial f(a, b)}{\partial b} = I[a < b]\]당연히 $a > b$일 때, $f(a, b)$가 $a$에 대한 identity func.이 되므로, 위의 결과는 당연하다!
4. sigmoid function $f(a) = \sigma(a)$
\[\frac{\partial f(a)}{\partial a} = \sigma(a) (1 - \sigma(a))\]Remark. generalized build block
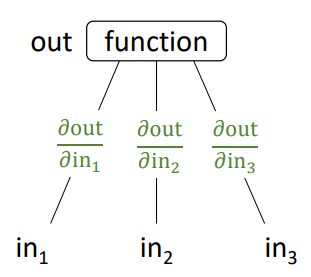
<Computational Graph>의 building block의 형태를 일반화하면 아래와 같다.
Remark. composing functions
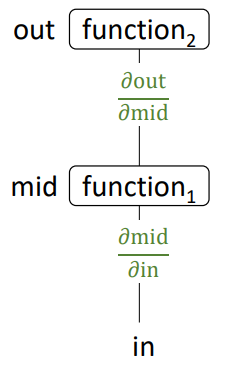
합성 함수의 경우도 <back-propagation>으로 쉽게 해결할 수 있다!
첫 block부터 살펴보자면, $\text{mid}$를 함수가 아니라 변수로 취급하면, 손쉽게 gradient를 구할 수 있다.
\[\frac{\partial \text{out}}{\partial \text{mid}}\]여기에서 그 다음 block을 살펴보면, 이것도 그냥 편미분을 수행해주면 되는 것이다.
\[\frac{\partial \text{mid}}{\partial \text{in}}\]두 gradient 값을 다 구했다면, 구한 gradient를 모두 곱해서 우리가 원하는 gradient를 구한다! 😁
\[\frac{\text{out}}{\text{in}} = \frac{\partial \text{out}}{\partial \text{mid}} \cdot \frac{\partial \text{mid}}{\partial \text{in}}\]Remark. Branching Block
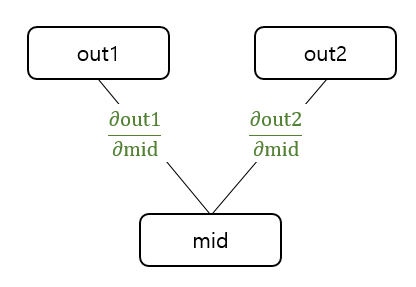
함수값이 두 군데로 분기하는 경우의 gradient는 아래와 같이 구할 수 있다.
\[\frac{\partial\text{out}}{\partial \text{mid}} = \frac{\partial\text{out1}}{\partial \text{mid}} + \frac{\partial\text{out2}}{\partial \text{mid}}\]즉, 분기하는 경우는 gradient 값을 더해주면 된다!
Example. Binary Classification with Hinge Loss
✨ Goal: $\dfrac{\partial \text{Loss}}{\partial \mathbf{w}}$
제일 먼저 할 일은 <Computational Graph>를 만드는 것이다. 그리고 그 다음에는 Graph의 edge에 규칙에 따라 계산한 gradient 값을 표시한다. 마지막에는 gradient를 구하고자 하는 대상, 여기서는 $\mathbf{w}$까지 Graph를 따라가며 edge에 표시된 gradient를 모두 곱해준다! 😁
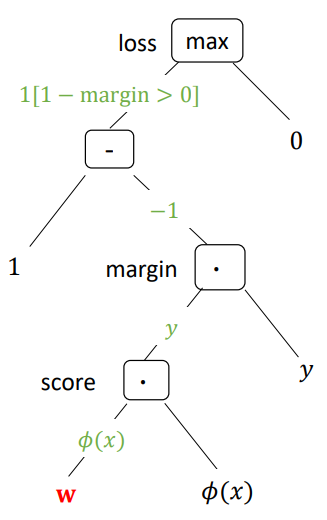
따라서 gradient는
\[\frac{\partial \text{Loss}}{\partial \mathbf{w}} = - 1 \cdot I(\text{margin} < 1) \cdot \phi(x) \cdot y\]