Bagging & Random Forest

2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

<Bagging>, <Boosting>, <Random Forest>를 아우르는 공통점은 모두 <ensemble model>이라는 점이다. <ensemble model>은 많은 weak learner를 결합해 strong learner를 디자인 하는 접근법이다. 많은 경우에 <ensemble model>가 single model보다 더 좋은 성능을 보인다 😁

Bagging

Bootstrap Sampling

<Bagging>을 살펴보려면, 먼저 <bootstrap sampling>에 대해 이해해야 한다.

간단하게 말하면, 기존의 샘플 $X = \{ (x_i, y_i) \}_i$에서 “sampling with replacement”로 뽑은 샘플을 말한다. <Bagging>에서는 이 <bootstrap sample>을 $Z$로 표기한다.

$Z^{(b)}$를 $b$번째 <bootstrap sample>이라고 한다면, <Bagging>은 각 bootstrap sample에 대해 estiamtor $\hat{f}^{(b)}(\, \cdot \, ; \, Z^{(b)})$를 구한다.

Bagging

<Bagging>은 “Bootstrap Aggregation”의 합성어이다. 대충 <bootstrap>을 종합(aggregate) 했다는 말이다.

Bagging estimator는 아래의 식으로 prediction을 진행한다.

\[\hat{f}_{\text{bag}}(x) = \frac{1}{B} \sum^B_{b=1} \hat{f}^{(b)}(x)\]

즉, bootstrap sample에서 디자인한 estiamtor의 평균으로 prediction 한다는 말이다. 심플하다!

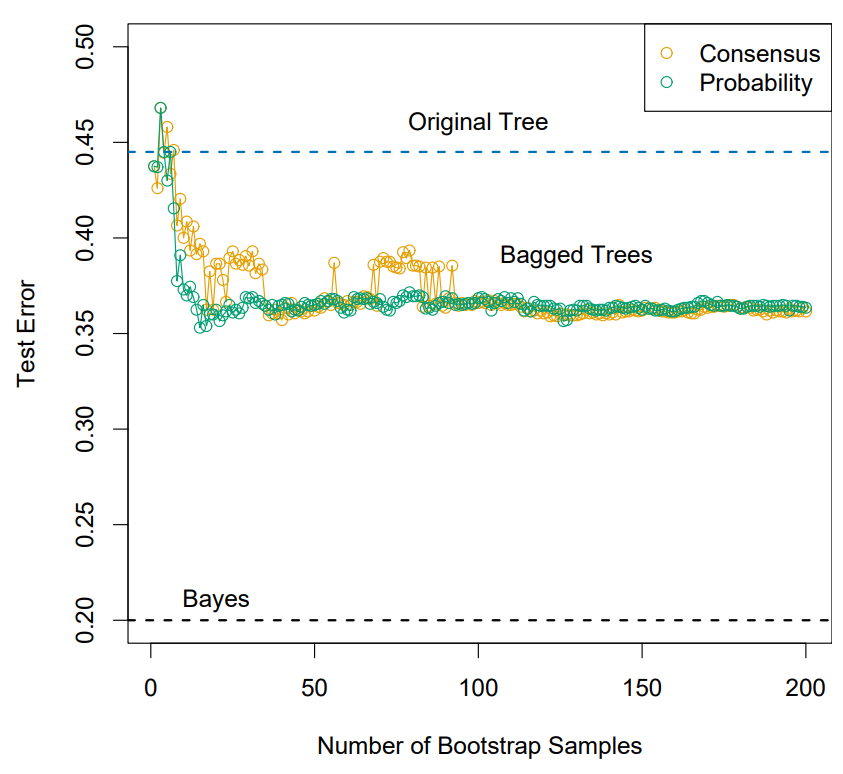
Model. Bagging for classification

<Bagging>으로 classification을 수행할 때는 두 가지 접근법이 있다: “consensus votes” & “averaging the probability”

“consensus votes”는 $\hat{f}^{(b)}(x)$에서 “# of 1”과 “# of 0”의 수를 비교해 많은 것을 취하는 접근이다.

“averaging the probability”는 개별 estimator가 확률을 predict하며, 전체 bagging estimator의 결과에 평균을 내는 방법이다.

Variance Reduction for Bagging

Let $f_A (x) = E_{\mathbf{Z}}\hat{f}(x)$ be the aggregated estimator. 이 $f_A (x)$는 실제 estimator가 아니라 논의의 편의를 위해 존재를 가정한 녀석이다!

우리가 현재 가지고 있는 bagging estiamtor인 $\hat{f}_{\text{bag}}$와 $f_A$의 성능을 비교하기 위해 error를 아래와 같이 정의하자.

\[e = E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - \hat{f}(X) \right]^2 \right]\] \[e_A = E_{Y, X} \left[ Y - f_A (X) \right]^2\]

Theorem.

With the squared error loss, $f_A$ always has a smaller risk than $\hat{f}$.

\[e \ge e_A\]

If each single classifier is unstable – that is, it has high variance, the aggregated classifier $f_A$ has a smaller variance than a single original classifier.

즉, 우리가 제대로 aggregate 했다면, 항상 그 error $e_A$는 항상 단일 estiatmor의 error $e$ 보다 작다는 정리이다.

proof.

\[\begin{aligned} e &= E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - \hat{f}(X) \right]^2 \right] \\ &= E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - f_A(X) + f_A(X) - \hat{f}(X) \right]^2 \right] \\ &= E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - f_A(X) \right]^2 + E_{Y, X} \left[ f_A(X) - \hat{f}(X) \right]^2 + 2 E_{Y, X} \left[ (Y - f_A(X)) (f_A(X) - \hat{f}(X)) \right] \right] \end{aligned}\]

이때, $2 E_\mathbf{Z} \left[ E_{Y, X} \left[ (Y - f_A(X)) (f_A(X) - \hat{f}(X)) \right] \right]$는

\[\begin{aligned} & 2 E_\mathbf{Z} \left[ E_{Y, X} \left[ (Y - f_A(X)) (f_A(X) - \hat{f}(X)) \right] \right] \\ &= 2 E_{Y, X} \left[ (Y - f_A(X)) \cdot E_\mathbf{Z} \left[ (f_A(X) - \hat{f}(X)) \right] \right] \\ &= 2 E_{Y, X} \left[ (Y - f_A(X)) \cdot (f_A(X) - E_\mathbf{Z} \hat{f}(X)) \right] \\ &= 2 E_{Y, X} \left[ (Y - f_A(X)) \cdot \cancel{(f_A(X) - f_A(X))} \right] \\ &= 0 \end{aligned}\]

따라서,

\[\begin{aligned} e &= E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - \hat{f}(X) \right]^2 \right] \\ &= E_\mathbf{Z} \left[ E_{Y, X} \left[ Y - f_A(X) \right]^2 + E_{Y, X} \left[ f_A(X) - \hat{f}(X) \right]^2 \right] \\ &= E_{Y, X} \left[ Y - f_A(X) \right]^2 + E_\mathbf{Z} \left[ E_{X} \left[ f_A(X) - \hat{f}(X) \right]^2 \right] \\ &\ge E_{Y, X} \left[ Y - f_A(X) \right]^2 = e_A \end{aligned}\]

이때, <Bagging>에 의해 개선된 정도는 아래와 같다.

\[E_\mathbf{Z} \left[ E_{X} \left[ f_A(X) - \hat{f}(X) \right]^2 \right] = \text{Var}\left( \hat{f}(X) - f_A(X) \right)\]

Remark.

• Increasing $B$ does not cause an overfitting
  • $B$가 커질 수록 평균에 가까워짐.
  • 반면에 Boosting은 $B$가 커질수록 overfitting 됨.
• 만약 individual tree가 크다면, 개별 tree가 overfitting 할 가능성은 있음.
• <Bagging>은 high-variance & low-bais 모델에서 좋은 성능을 냄.
• In practice, <Boosting> is better than <Bagging> in many examples.
  • <Bagging>을 변형한 모델인 <Random Forest>를 사용하면, <Boosting>과 비슷한 정도의 성능을 낼 수 있다고 함!

---

Random Forest

<Bagging>에서 개별 DT는 모두 동일한 분포를 갖는다. 그래서 “bagged estimator”는 개별 bootstrap tree와 동일한 bias를 갖는다.

이때, <Bagging> 모델의 “variance”를 줄일 수 있는 방법은 개별 bootstrap tree 사이의 correlation을 줄여 모델을 개선할 수 있다!!! 😁

The ‘average’ of $B$ iid random variables with variance $\sigma^2$ has variance $\sigma^2/B$. (당연!)

이번에는 iid sample이 아닌 경우를 살펴보자! $\text{Var}(X_i) = \sigma^2$이고, pairwise correlation은 $\text{Corr}(X_i, X_j) = \rho$인 경우다!

The ‘average’ of $B$ identically distributed random variables with variance $\sigma^2$ and pairwise correlation $\rho$ has variance

\[\rho \sigma^2 + \frac{1-\rho}{B} \sigma^2\]

이때, 이것과 iid인 경우에서의 variance $\sigma^2/B$를 비교해보자.

\[\text{Var} \left( \frac{X_1 + \cdots X_B }{B} \right) = \rho \sigma^2 + \frac{1-\rho}{B} \sigma^2 \quad \text{vs.} \quad \frac{\sigma^2}{B}\]

만약 correlation $\rho$가 0이라면, iid인 경우와 같다.

\[0 \sigma^2 + \frac{1-0}{B} \sigma^2 = \frac{\sigma^2}{B}\]

만약 correlation $\rho$가 1인 경우, 즉 $X = X_i$라면,

\[\rho \sigma^2 + \frac{1-1}{B} \sigma^2 = \sigma^2 > \frac{\sigma^2}{B}\]

따라서, sample이 correlate 되어 있다면, variance는 더 커진다.

\[\rho \sigma^2 + \frac{1-\rho}{B} \sigma^2 \ge \frac{\sigma^2}{B}\]

<Bagging>은 bootstrap sample로 DT를 구성한다. 이때, bootstrap sample은 sampling with replacement이기 때문에 개별 DT를 만들기 위해 사용한 input의 일부는 항상 어느 정도 겹칠 것이다. 따라서, <Bagging>의 개별 DT는 서로 positively correlated 되어 있다! RF는 이런 correlation을 줄여 Bagging을 개선한다!!

Before each split in bagging DT, RF selects $m \le p$ of input variables at random as cadidates for splitting. 즉, 변수 중 일부만 쓰기 때문에, 개별 DT끼리 변수가 겹칠 확률이 줄어든다!

RF의 경우, 일부의 변수만 사용하기 때문에 <bagging>보다 더 빠른 속도를 보인다!

---

Out of Bag Error

이번에는 <Bagging>과 <Random Forest>에서 cross-validation을 수행하는 방법인 <OOB error; Out of Bag error>에 대해 소개한다.

<Bootstrap sample>의 경우, sampling with replacement이기 때문에 1,000개의 전체 샘플 중에 800만 쓰이고, 남은 200개가 안 쓰이게 되는 경우가 발생할 수 있다. 그래서 Bagging, RF에서는 이런 “out of bag”한 샘플들을 가지고 validation error를 측정할 수 있다!!

그래서 Bagging, RF는 <OOB error>가 stabilize하는 순간에 training을 종료한다!