Model-based Clustering
2021-1학기, 대학에서 ‘통계적 데이터마이닝’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
앞에서 살펴본 <K-means>와 <hierarchical> clustering은 휴리스틱 기법에 속한다. 어떤 모델이 있는 것이 아니기 때문에, statistical inference 역시 불가능하다. 또한, 실전에서는 categorical variable 때문에 “dissimilarity measure”를 정의하는 것도 쉽지 않다.
<Model-based cluastering>은 데이터셋의 모델, 즉 PDF $\text{Pr}(x)$을 estimation 하는 기법이다!
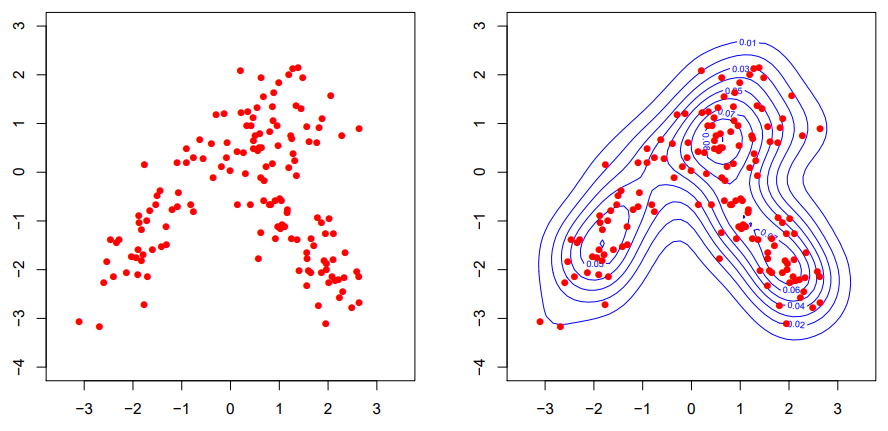
2차원 데이터에서 non-parameteric method로 $\text{Pr}(x)$를 추정하는 것은 어렵지 않다!
Mixture Model
2차원 데이터에서 PDF $\text{Pr}(x)$를 추정하는 것은 어렵지 않다. 그러나 3차원부터는 PDF를 추정하기 쉽지 않으며, 이것을 visualize 하는 것도 clustering 하는 것도 힘든 일이다.
이런 고차원에서의 문제를 해결하기 위해 쓰는 기법이 바로 <Mixture Model>이다! 참고로 <Mixture Model>은 “parameteric” 기법이다.
Let $P = \{ f_{\phi}(\cdot) : \phi \in \mathcal{P} \}$ be a parameteric model. 이때, $f_{\phi}(x)$는 어떤 pdf로 예를 들면, 이런 형태다:
\[f_{\phi}(x) = N(x \mid \mu, \sigma^2)\]$f_{\phi}(x)$에서 $\phi$는 parameter이며, 집합 $P$는 가능한 모든 $\phi$에 대한 PDF의 모음인 것이다.
이번에는 $K$-cluster를 표현하는 parameteric PDF를 $f_{\phi_k}(x)$라고 할 때, 아래와 같은 PDF의 모음; collection of densities를 정의해보자. 별건 아니고, 그냥 cluster PDF의 가중합의 조합이다.
\[\left\{ \sum_{k=1}^K \pi_k f_{\phi_k}(\cdot) \; : \; \phi_k \in \mathcal{P}, \pi_k > 0, \sum_{k=1}^K \pi_k = 1\right\}\]이것을 <K-component mixture model>이라고 한다! 이때, $\pi_k$를 “mixing proportion”이라고 한다.
💥 NOTE: 위에서 정의한 <K-component mixture model> 역시 PDF가 된다. 증명은 확률合이 1이 되는지 확인해보면 되는데, 쉽다.
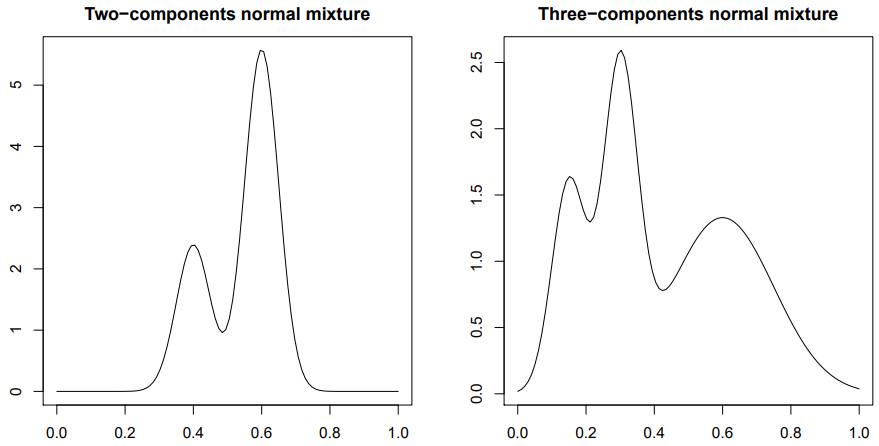
component를 몇개 쓰는지에 따라 분포에서 나타나는 mode의 최대 갯수가 달라진다.
Let $X_1, \dots, X_n$ be iid from a <K-component mixture>; Data point $X_i$가 mixture model에서 샘플링 되었다고 가정한다.
우리는 Data points $\{ X_1, \dots, X_n \}$로부터 parameter $\theta$를 추정해야 한다. 현재 우리는 $\theta$를 모르는(unknown) 상태며, 그 형태는 아래와 같다.
\[\theta = (\pi_1, \dots, \pi_K, \; \phi_1, \dots, \phi_K)^T\]우리는 이 unknown parameter $\phi$를 추정하기 위해 MLE를 사용할 것이다.
Algorithm. MLE
Find $\theta$ such that maximize $\ell(\theta)$.
아마 보통의 MLE 문제는 위의 log-likelihood function에 편미분 해서, optimal solution을 찾는다. 하지만, 이 문제의 경우, 찾아야 하는 변수가 $2K$ 정도 되기 때문에, 편미분으로는 쉽게 풀 수 없다. 심지어 Gradient Descent 같은 numerical method를 쓰는 것 역시 어렵다고 한다.
그러나 방법은 있다!! 이런 문제를 풀기 위해 우리는 <EMAlgorithm; Expectation-Maximization>을 사용할 것이다!! 😎
EM Algorithm
먼저 <EM Algorithm>이 뭔지 그 정의부터 살펴보자.
EM is a general algorithm to find the MLE when a part of data is missing.
EM에서는 이런 missing data를 잠재변수, “latent variable” $Z$라고 한다. 그래서 EM에서 쓰는 데이터 $Y$는 아래와 같이 표현된다.
Let $Y = (X, Z)$ be a random vector following a density $p_{\theta}(\cdot)$ where $X$ is the “obsesrved data” and $Z$ is the “missing data”.
missing data $Z$가 도입되었지만, 여전히 우리의 목표는 observed data $X$로 likelihood를 최대값으로 만드는 $\theta$를 찾는 것이다!
Let $\ell(\theta; X, Z) = \log p_{\theta}(Y)$ be the “complete log-likelihood”; 먼저 $X$와 $Z$를 모두 사용하는 log-likelihood function을 정의한다.
여기서 잠깐 Insight를 얻고 가자. ‘Lee-jaejoon’님의 포스트의 포스트를 많이 참고했다.
1. 만약 모든 확률변수가 관측 가능했다면, 즉, $Z = \emptyset$.
우리는 $\theta$의 값을 추정하는 $\hat{\theta}$를 얻을 수 있었을 것이다.
그러나 우리는 관측하지 못한 $Z$가 존재하므로, $\theta$의 값을 추정할 수 없다.
2. 만약 $\theta$의 값을 알고 있었다면,
우리는 이걸로 확률분포를 완전히 특정할 수 있기 때문에, 관측되지 않은 $Z$의 분포도 알 수 있다.
그러나 parameter $\theta$는 unknown이기 때문에 $Z$의 분포 역시 알 수 없다.
즉, 현재의 상황은 $Z$를 모르니 $\theta$를 모르고, 반대로 $\theta$를 모르니 $Z$를 모르는 상황이다.
<EM Algorithm>은 “만약 $\theta$를 안다면?”라는 아이디어로 이 상황을 해결한다.
Algorithm. EM Algorithm
1. Initialize Parameter
\[\theta \leftarrow \theta^{(0)}\]2. Expectation Step; E-Step
만약 우리가 $\theta$의 값이 $\theta^{(0)}$라는 것을 알고 있다면, 또 관측한 데이터 $X$가 있다면, 우리는 이를 통해 관측하지 못한 missing data $Z$의 ‘조건부 분포‘을 구할 수 있다.
\[\text{Pr}(Z \mid X = x, \; \theta = \theta^{(0)})\]is a conditional distribution of $Z$ given $X=x$ and $\theta = \theta^{(0)}$.
우리는 이 $Z$의 조건부 분포를 활용해 log-likelihood에서 $Z$를 marginalize 시킬 것이다. 이것은 우리가 모르는 $Z$를 없애주기 때문에 충분히 그럴듯한 접근이다! 이것을 표현하면 아래와 같다.
\[E_{Z \mid X, \theta^{(0)}} \; \ell(\theta; X, Z) = \sum_{Z} \ell(\theta^{(0)}; X=x, z) \cdot p_{\theta^{(0)}} (z \mid X=x)\]이것은 missing data $Z$에 가능한 값들에 대한 평균적인 log-likelihood이다. 즉, $Z$가 정확히 어떤 값을 갖는지는 모르지만, $Z$가 가질 수 있는 값들에 대해 log-likelihood가 평균적으로 어떤 양상인지를 나타내주는 ‘함수’다.
우리는 이것을 ‘log-likelihood의 대타’라는 의미에서 “surrogate function” $Q(\theta \mid \theta^{(0)}$라고 부른다.
\[Q(\theta \mid \theta^{(0)}) = E_{Z \mid X, \theta^{(0)}} \; \ell(\theta; X, Z)\]3. Maximization Step; M-Step
이제 우리는 $Z$를 marginalize out한, missing data에서 자유로운 surrogate function $Q(\theta \mid \theta^{(0)})$를 가지고 있다. 우리를 이 $Q(\theta \mid \theta^{(0)})$를 마치 우리가 본래 목표로 했던 likelihood 함수로 취급에 이것에 대해 maximize 하는 $\theta$를 찾아줄 것이다. 그리고 그런 $\theta$를 찾았다면, 그것을 새로운 $\theta$ 값으로 사용한다!!
\[\theta^{(1)} = \underset{\theta}{\text{argmax}} \; Q(\theta \mid \theta^{(0)})\]4. Repeat Until Converge!
지금은 바쁘니, 추후에 마무리 하겠습니다!
