SVM; Support Vector Machine
본 글은 2020-2학기 “컴퓨터 비전” 수업의 내용을 개인적으로 정리한 것입니다. 지적은 언제나 환영입니다 :)
💥 (before start) SVM에서는 class label이 $\{ -1, +1\}$로 인코딩 되어 있다고 가정한다.
Introduction to SVM
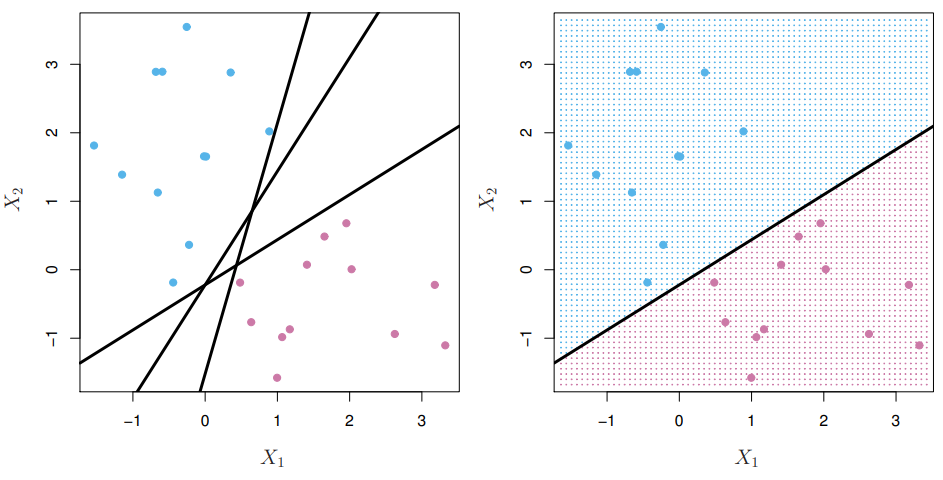
Linearly Separable한 데이터 포인트의 집합이 있을 때, 두 집합을 나누는 hyper-plane은 무한히 많이 그릴 수 있다. <SVM; Support Vector Machine>은 무한히 많은 hyper-plane 중 어떤 것이 가장 best인지 찾는 분류 알고리즘이다.
<SVM>에서는 best hyper-plane을 아래와 같이 정의한다.
즉, <SVM>은 “margin“을 최대화하는 hyper-plane인 것이다. 그럼 “margin“은 무엇일까? 쉽게 설명하면, 데이터를 선형으로 분리하는 hyper-plane에서 가장 가까운 데이터의 거리 “margin“이라고 한다.
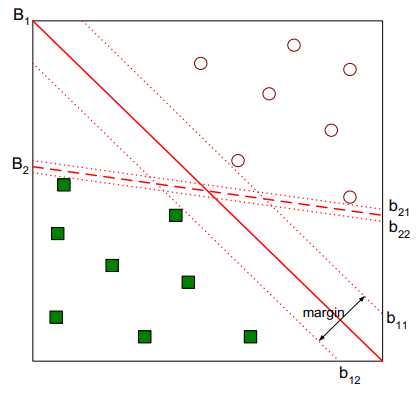
위 그림을 보면, $B_1$과 $B_2$ 모두 데이터셋을 잘 분할하고 있지만, $B_1$이 $B_2$ 보다 더 여유롭게 분리하고 있는 것을 볼 수 있다. 이때, 얼마나 여유롭게 분리하고 있는지를 hyper-plane과 가장 가까운 데이터의 거리로 수치화할 수 있으며, 이것이 바로 “margin“이다.
“margin”에 대한 식을 유도하기 위해 hyper-plane을 아래와 같이 정의해보자.
\[w^T x + b = 0\]이때, $w$는 hyper-plane의 법선벡터다.
hyper-plane을 잘 정의했으면, “margin“은 “점과 평면 사이 거리 공식“을 통해 쉽게 구할 수 있다.
* 만약 margin의 방향을 구분하고 싶다면, 분자 부분의 절댓값을 쓰지 않으면 된다!
또는 위의 식을 약간 변형해 아래와 같이 사용할 수도 있다.
\[\text{dist}(x_0) = \frac{ y_0 \cdot (w^T x_0 + b) }{ \| w \| }\]사실 우리가 평소에 쓰는 “margin”의 개념은 위의 식에서 분자인 $y_0 \cdot (w^T x_0 + b)$이다. 이 “margin”은 class label이 correctly classified 되었다면, 항상 양수의 값을 갖는다. (linearly separable)한 SVM에서는 이 margin 값이 항상 양수다!
위의 점-평면 거리 공식을 바탕으로 ‘the minimal distance’인 “margin“을 표현하면 아래와 같다.
\[\begin{aligned} \text{margin} &= \min_i \left[ \text{dist}(x_i) \right] \\ &= \min_i \left[ \frac{ y_i \cdot (w^T x_i + b) }{ \| w \| } \right] \\ &= \frac{1}{\| w \|} \min_i \left[ y_i \cdot (w^T x_i + b) \right] \end{aligned}\]이에 위에서 유도한 “margin”에 대한 식으로 <SVM>의 최적화 문제를 기술하면 아래와 같다.
\[\underset{w, b}{\text{argmax}} \left[ \frac{1}{\| w \|} \min_i \left[ y_i \cdot (w^T x_i + b) \right] \right]\]이제 <SVM>의 최적화 문제를 정의했으니, 이 문제의 solution을 찾아보자!
Convex Optimization
\[\underset{w, b}{\text{argmax}} \left[ \frac{1}{\| w \|} \min_i \left[ y_i \cdot (w^T x_i + b) \right] \right]\]먼저, <SVM>의 최적화 식에서 약간의 normalization을 수행해준다.
그 이유는 hyper-plane $w^T x + b$나 $c(w^T x + b)$나 동일한 평면을 정의하기 때문에, 문제의 자유도를 낮추고 식을 풀기 쉽게 변형하기 위함이다!
우리는 아래의 조건을 만족하는 $w$와 $b$로 hyper-plane의 식을 normalize 한다.
\[w^T x_{+} + b = 1 \quad \text{and} \quad w^T x_{-} + b = -1\]이때, $x_{+}$와 $x_{-}$는 hyper-plane이 분할하는 label에서 “margin”을 이루는 점이다. 우리는 이 점을 “support vector“라고 부른다!
ps) 본인은 위와 같이 두 support vector에 대한 값이 $\pm1$이 되도록 norm하는게 가능한지 잘 이해가 안 되었는데, 잘 생각해보니까 두 support vector가 같은 margin을 가지도록 설정하면 되는 거였다.1 다르게 생각하면, 위와 같이 normalize 하는 것 역시 최적화 식에 constraint로 작용할 거라는 생각이 든다.
위와 같이 설정하면, 곧 아래의 식이 성립한다.
\[\text{margin} = \frac{1}{\| w \|}\]이를 바탕으로 <SVM>의 최적화 식을 다시 쓰면 아래와 같다. 우리가 “support vector”의 값이 $\pm1$이 되도록 설정했기 때문에 기존 식에서 “constraint” 텀이 붙는다.
\[\underset{w, b}{\text{argmax}} \frac{1}{\| w \|} \cdot 1 \quad \text{subject to} \quad y_i (w^T x_i + b) \ge 1 \;\; \forall i\]이때 위의 최적화 식은 아래의 convex optimization과 동치다.
\[{\color{red}{\underset{w, b}{\text{argmin}} \frac{1}{2} \| w \|^2}} \quad \text{subject to} \quad y_i (w^T x_i + b) \ge 1 \;\; \forall i\]Dual Problem
위의 과정을 통해 우리는 <SVM>을 “Convex Optimization” 문제의 형태로 잘 유도했다.
\[\min_{w, b} \frac{1}{2} \| w \|^2 \quad \text{subject to} \quad y_i (w^T x_i + b) \ge 1 \;\; \forall i\]이때, “Convex Optimization” 문제에 “Lagrange Multiplier” $\lambda_i$를 도입하면 <Dual Problem>이라는 새로운 최적화 문제를 얻는다. 이것을 <Dual Problem>이라고 하며 <SVM>의 경우는 아래와 같다.
\[\max_{\lambda} \left[ \min_{w, b} L(w, b, \lambda) \right] \quad \text{where} \quad L(w, b, \lambda) = \frac{1}{2} \| w \|^2 - \sum_{i=1}^n {\color{red}{\lambda_i}} \{ y_i (w^T x_i + b) - 1 \} \quad \text{and} \quad \lambda_i \ge 0\]Lagrange Multiplier $\lambda_i$를 도입하면서, 기존 식의 constraint 부분이 식 $L(w, b, \lambda)$로 흡수 되었다.
식이 기존보다 훨씬 복잡해졌지만, 위의 식은 정말 생각보다 너무 쉽게 풀린다!! 😲
\[\frac{\partial L(w, b, \lambda)}{\partial w} = w - \sum_{i=1}^n \lambda_i y_i x_i = 0 \quad \iff \quad w = \sum_{i=1}^n \lambda_i y_i x_i\] \[\frac{\partial L(w, b, \lambda)}{\partial b} = 0 - \sum_{i=1}^n \lambda_i y_i = 0 \quad \iff \quad \sum_{i=1}^n \lambda_i y_i = 0\]와우 정말 간단하지 않은가?? 이것은 우리가 Lagrange Multiplier를 도입하면서, constraint를 흡수했기 때문에 단순히 편미분 만으로 최적화 식의 해(解)를 구할 수 있는 것이다!! 😆
하지만 아직 문제를 완전히 해결한 것은 아니다. 최적의 $w$는 찾았지만, 그 식에 $\lambda_i$가 있어 완전한 解를 얻은 것이 아니다. 위의 과정은 기존의 <Dual Problem>의 최적화 문제를 아래와 같이 한꺼풀 벗긴 것에 불과한다.
\[\begin{aligned} &\max_{\lambda} \left[ \frac{1}{2} \| w \|^2 - \sum_{i=1}^n \lambda_i \{ y_i (w^T x_i + b) - 1 \} \right] \\ &\text{where} \quad w = \sum_{i=1}^n \lambda_i y_i x_i \quad \text{and} \quad \sum_{i=1}^n \lambda_i y_i = 0 \quad \text{and} \quad \lambda_i \ge 0 \end{aligned}\]이때 위의 식에서 $\sum \lambda_i y_i = 0$를 적용해 식의 오른쪽 텀을 아래와 같이 만들 수 있다.
\[\max_{\lambda} \left[ \frac{1}{2} \| w \|^2 - \sum_{i=1}^n \lambda_i ( y_i w^T x_i - 1 ) \right] = \max_{\lambda} \left[ \frac{1}{2} \| w \|^2 - \sum_{i=1}^n \lambda_i y_i w^T x_i + \sum_{i=1}^n \lambda_i \right]\]이번에는 $w = \sum \lambda_i y_i x_i$를 대입하자.
\[\begin{aligned} \max_{\lambda} \left[ \frac{1}{2} \| w \|^2 - \sum_{i=1}^n \lambda_i y_i w^T x_i + \sum_{i=1}^n \lambda_i \right] &= \max_{\lambda} \left[ \frac{1}{2} \| \sum_{i=1}^n \lambda_i y_i x_i \|^2 - \sum_{i=1}^n \lambda_i y_i \sum_{j=1}^n \lambda_j y_j x_j^T x_i + \sum_{i=1}^n \lambda_i \right] \\ &= \max_{\lambda} \left[ \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j x_i^T x_j - \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j x_i^T x_j + \sum_{i=1}^n \lambda_i \right] \\ &= \max_{\lambda} \left[ \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j x_i^T x_j \right] \end{aligned}\]식을 정리하면 아래와 같다.
\[\begin{aligned} \max_{\lambda} \left[ \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j x_i^T x_j \right] \\ \text{where} \quad \lambda_i \ge 0 \quad \text{and} \quad \sum_{i=1}^n \lambda_i y_i = 0 \end{aligned}\]위의 최적화 문제의 解는 <QP; Quadratic Programming)>로 얻을 수 있다며, 그때의 解 $\lambda^{*}$는 아래와 같다.
\[\begin{aligned} \lambda^{*} = \underset{\lambda}{\text{argmax}} \; \left[ \sum_{i=1}^n \lambda_i - \frac{1}{2} \sum_{i=1}^n \sum_{j=1}^n \lambda_i \lambda_j y_i y_j x_i^T x_j \right] \\ \text{where} \quad \lambda_i \ge 0 \quad \text{and} \quad \sum_{i=1}^n \lambda_i y_i = 0 \end{aligned}\]이제, solution $\lambda^{*}$대입하면 $w$, $b$에 대한 解를 얻을 수 있다.
\[w^{*} = \sum_{i=1}^n \lambda^{*}_i y_i x_i\]이때 $\lambda^{*}_i$는 0 또는 양수의 값을 갖는데,
- If $\lambda^{*}_i = 0$, then $x_i$는 hyper-plane을 정의하는데 기여하지 않는다.
- If $\lambda^{*}_i > 0$, then $x_i$는 hyper-plane을 정의하는데 기여하고, 이것을 “support vector“라고 부른다!
$b^{*}$는 $w^T x_{+} + b = 1$의 식을 통해 유도하면 된다. 따로 식을 제시하지는 않겠다.
Soft-margin SVM
만약 데이터셋이 linearly separable 하지 않다면, 위의 <SVM>의 解를 구할 수 없다! 🤯 이런 경우를 해결하기 위해 <slack variable> $\xi_i$를 도입한다! 그 결과, <SVM>에 대한 식은 아래와 같은 최적화 문제가 된다.
\[\begin{aligned} \min_{w, b, \xi} \frac{1}{2} \| w \|^2 &+ C \sum_{i=1}^n \xi_i\\ \text{subject to} &\quad y_i (w^T x_i + b) \ge 1 - \xi_i \;\; \forall i, \quad \text{and} \quad \xi_i \ge 0 \end{aligned}\]이것은 support vector가 만드는 margin 영역보다 더 안쪽에 몇개의 데이터 포인트가 존재할 수 있도록 만들어 준다!
\[y_i (w^T x_i + b) \ge 1 - \xi_i\]쉽게 생각해 데이터셋을 non-separable 하게 만드는 데이터포인트에 대해선 $\xi_i$가 양수의 값을 가져 그들의 margin 값이 조금 작아져도 허용한다고 이해해도 될 것 같다.
Non-Linear SVM
-
물론 어느 한쪽의 support vector가 더 짧을 수도 있겠지만, 그것은 SVM의 취지에 어긋나므로 기각한다. ↩
