All Pairs Shortest Paths; Floyd-Warshall

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

---

우리가 지금까지 살펴본 “Shortest Path” 문제는 모두 출발 노드 $s$와 도착 노드 $t$가 고정된 경우였다. 그러나 때로는 주어지는 노드 쿼리 $(s, t)$에 대한 shortest path를 찾거나 또는 그래프에 존재하는 모든 노드 쌍 $(u, v)$ 사이의 shortest path를 찾고 싶을 수 있다.

만약 이것을 <Dijkstra Algorithm>을 사용해 $V$개의 노드에 대해서 “single-source shortest path”를 찾고자 한다면, 총 $V \times O(VE) = O(V^2 E)$의 시간이 걸린다.

그.러.나. <DP>를 사용하면, 좀더 빠른 시간 안에 문제를 해결할 수 있다!! 😁 이 알고리즘을 <Floyd-Warshall Aglrorithm>라고 한다.

---

우리는 두 정점 $(i, j)$을 잇는 최단 경로를 아래와 같이 경유지 $k$를 거치는 문제로 생각해볼 수 있다!!

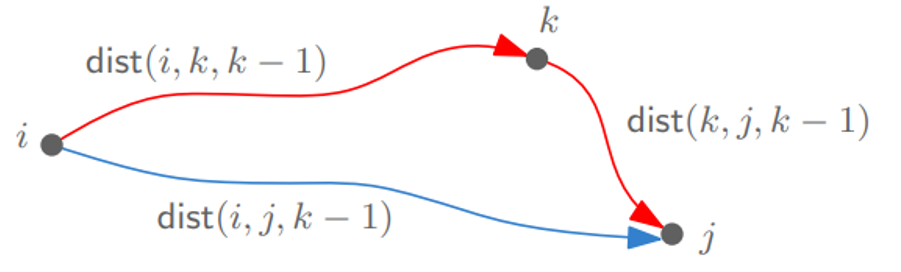
즉, 두 정점을 잇는 최단 경로를 $k-1$까지의 노드를 사용하는 경우와 $k$까지 노드를 포함해 사용한 경우(pass through $k$)로 나누어 둘 중 최단 경로를 선택한다.

이때, 주의할 점은 이렇게 경유지를 거쳐가는 방법을 사용하기 위해선 경유하는 경로를 이루는 sub-path 역시 최단 경로임이 보장되어야 한다!

이를 알고리즘으로 표현하면 아래와 같다.

// initialize
for all $(i, j) \in E$
  $\text{dist}(i, j, 0) = \ell(i, j)$

for $k=1$ to $n$:
  for $i=1$ to $n$:
    for $j=1$ to $n$:
      $\text{dist}(i, j, k) = \min \{ \text{dist}(i, j, k-1), \; \text{dist}(i, k, k-1) + \text{dist}(k, j, k-1)\}$

사실 실제로 구현을 해보면, 3차원 배열이 아니라 $k$를 없앤 2차원 배열로도 충분히 잘 동작한다 😉

시간 복잡도는 기존 DFS 기반의 $O(V^2 E)$에서 $O(V^3)$로 줄어들었다!! (일반적으로 sparse graph가 아니라면 $V < E$이다.)

---

구현

• adjacency matrix로 연결성을 표현하는 걸 추천
• adjacency matrix 초기화 잊지 말것; fill();
  • 초기화 할 때, INT_MAX와 같이 매우 큰수로 하게 되면 overflow 때문에 잘못된 결과를 뱉음;;
• 구현 자체는 정말 간단함! LIS, edit distance 급으로 쉬운 구현!

// initialization 1
fill(&dist[0][0], &dist[N+1][N+1], MAX2);

// initialization 2
for (int i = 0; i < M; i++) {
  int a, b;
  scanf("%d %d", &a, &b);

  dist[a][b] = 1;
  dist[b][a] = 1;
}

// Floyd-Warshall
for (int k = 1; k <= N; ++k) {
  for (int i = 1; i <= N; ++i) {
    for (int j = 1; j <= N; ++j) {
      if(dist[i][k] == MAX2 || dist[k][j] == MAX2) continue;

      dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
    }
  }
}

---

참고로 <Flyod-Warshall>은 노드의 수가 10,000가 되면 너무 많은 메모리를 쓰기 때문에 쓸 수 없다! 백준 1325번: 효율적인 해킹이 메모리 때문에 <Flyod-Warshall>을 쓸 수 없는 예이다!

추천 문제

• 백준 1389번: 케빈 베이컨의 6단계 법칙
• 백준 11404번: 플로이드
• 백준 11562번: 백양로 브레이크
• 백준 1507번: 궁금한 민호 // 플로이드-와샬을 어떻게 써야할지 고민을 좀 해야 했다
• 백준 1238번: 파티 // 사실 그냥 다익트스라로 풀어도 된다