Shortest Reliable Paths
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)
주어진 그래프 $G$에서 최대 $k$개의 edge를 거쳐 노드 $s$에서 노드 $t$로 가는 shortest path를 찾고 싶다. 이전의 <Dijkstra Algothm>의 상황과 비슷하지만, 최대 $k$개의 edge를 거친다는 조건이 추가 되었다. 아래의 그래프를 통해 살펴보면, $B$에서 $T$로 갈 때, 최대 $1$개의 edge만 거칠 수 있다면, 비용이 $4$인 edge를 거쳐서 도착해야 한다. 이것은 “at most $k$ edge”라는 조건 때문에 the shortest path인 $(B, D, T)$의 비용 $2$보다 더 큰 비용을 지불하게 된 것이다.
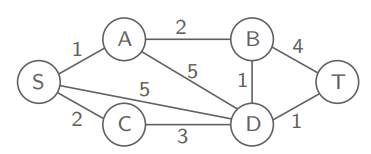
이 문제는 <DP> 기법을 사용해 $k$를 점진적으로 증가시키며 풀 수 있다. 시작노드 $s$에서 각 노드 $v$까지 $k$개의 edge를 거쳤을 때, 즉 $k$-hop을 했을 때의 shortest cost를 dist[v][k]에 저장하면 된다.
Let $\text{dist}(v, i)$ be the shortest path from $s$ to $v$ that uses $i$ edges.
(Initialize) set $\text{dist}(v, 0) = \infty$ and $\text{dist}(s, *) = 0$.
Then,
\[\text{dist}(v, i) = \min_{(u, v) \in E} \left\{ \text{dist}(u, i-1) + \ell(u, v) \right\}\]시작노드 $s$에서 시작해보자. 그러면, 당연하게도 모든 $v$에 대해 $\text{dist}(v, 1) = \ell(s, v)$가 성립한다.
다음은 $s$의 인접 노드였던 $v$ 노드들에 대해 그들의 인접 노드 $u$들의 $\text{dist}(u, 2)$ 값을 갱신한다.
<Dijkstra’s Algorithm>의 경우 몇 번 hop 했는지를 따로 기록하지 않고 dist[v]를 기준으로 답을 찾기 때문에 hop 정보를 알 수 없다. 물론 약간 수정하면 <Dijkstra’s Algorithm>에서 dist[v] = (cost, hop)를 저장해서 hop 정보를 기록할 수 있다.
그러나 이번 경우는 dist[v][hop]을 저장하기 때문에 도착노드 $t$에 대해 dist[t][hop]에서 원하는 hop 수에 따른 cheapest cost를 얻을 수 있는 것이다.
결국 1차원 dist[] 배열을 2차원 dist[][]로 확장, 메모리를 더 사용해서 hop 정보를 저장한 것이다. <Dijkstra’s Algorithm>의 원리와 크게 다르지 않다.
* 문제에서 요구한게 “exact $k$ edges”가 아니라 “at most $k$ edge”라는 점을 기억하자!
추천 문제
안타깝게도 백준에서 관련된 문제를 찾지 못 했다 😥