Independent Sets in Tree
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
그래프 $G$에서 <Independent Set; 독립집합>은 아래와 같이 정의한다.
Definition. Independent Set
Given a graph $G = (V, E)$, a subset $S \subset V$ is an <independent set> if there are no edges between nodes in the subset $S$.
<Independent Set Problem>은 그래프에서 가능한 독립집합 중 가장 큰 집합을 찾는 문제를 말한다. 일반적으로 <Independent Set Problem>를 polynomial time으로 푸는 것은 불가능하다. 이것에 대해서는 <NP-complete>에 대해 다룰 때 다시 언급하도록 하겠다.
그러나 만약 그래프 $G$가 tree라면, <Independent Set Problem>를 linear time으로 해결할 수 있다!!
먼저 첫 번째 경우는 트리의 노드에 가중치가 없는 경우다. 문제를 묘사하면 아래와 같다.
당신은 회사 파티를 주최하려 한다. 최대한 많은 사람을 초대하려 하지만 각각의 사람들은 바로 직속 상사가 파티에 올 경우 파티에 오지 않는다.
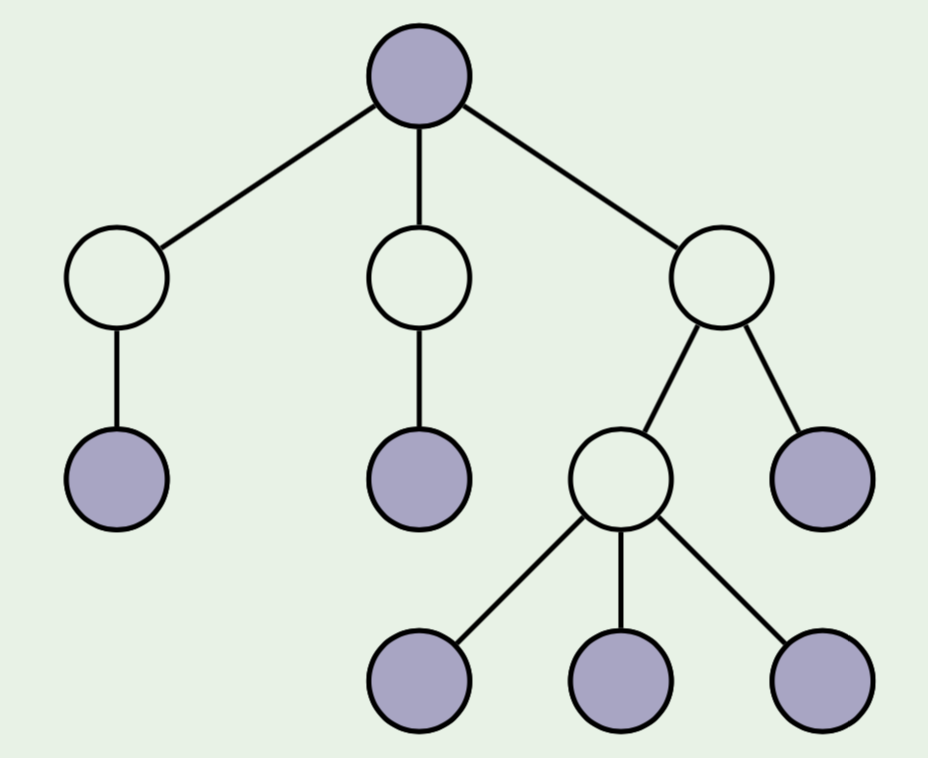
이 경우, greedy 하게 접근하여 문제를 해결할 수 있다!
while $T$ is not empty:
take all the leaves to the solution.
remove them and their parents from $T$.
return the constructed solution.
두 번째 경우는 트리의 노드에 가중치가 존재하는 경우다. 문제를 묘사하면,
위의 문제와 상황은 똑같으나 파티에 오는 사람마다 매력적인 정도가 있어서 이 매력도의 合을 최대로 하고자 한다.
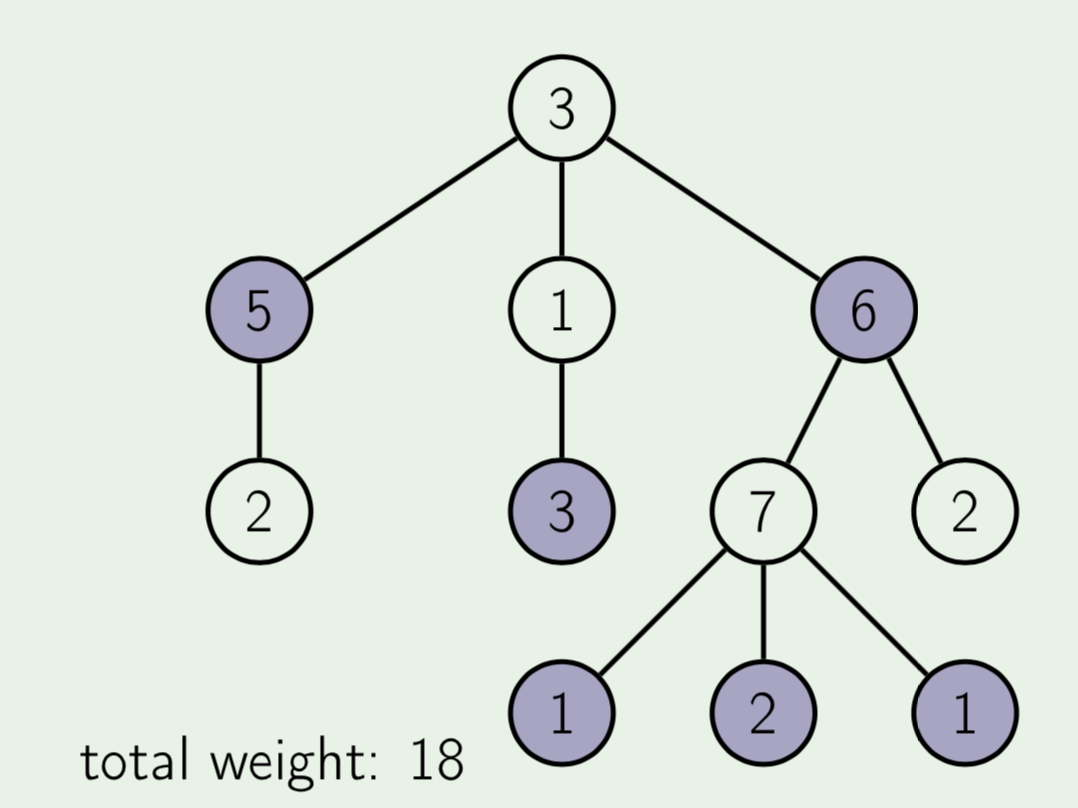
이 경우는 DP를 통해 문제를 해결할 수 있다!!
노드 $s$를 root로 하는 sub-tree의 Maximum Weight Ind. Set은 아래와 같이 구할 수 있다.
\[D(s) = \max \left\{ \sum_{\text{child $v$ of $s$}} D(v), \; w(s) + \sum_{\text{grandchild $u$ of $s$}} D(u) \right\}\]구현
벡준 2213번: 트리의 독립집합를 기준으로 구현한 코드를 해설해보겠다.
먼저 Maximum Weight Sum of Ind. Set $D(u)$의 값을 저장할 DP 배열을 구상한다.
int dp[VMAX][2]; // Maximum Weight Sum of Ind. Set
이때, dp[i][0]는 $i$번째 노드를 포함하지 않았을 때, dp[i][1]는 $i$번째 노드를 포함했을 때의 Maximum Weight Sum이다.
문제를 해결하기 위한 재귀함수는 아래와 같다.
int root = 1; // 어느 노드를 root로 사용하든 상관 X
travel(root, -1);
void travel(int node, int par) {
dp[node][0] = 0;
dp[node][1] = weight[node];
IndSet[node][1].push_back(node);
// visit children
for (int i = 0; i < edges[node].size(); i++) {
int child = edges[node][i];
if (child == par) continue; // root node
travel(child, node); // recursion
// exclude root node -> use child or not -> use `dp[child][0]` or `dp[child][1]`
bool whichBigger = dp[child][1] >= dp[child][0];
dp[node][0] += dp[child][whichBigger];
for (int j = 0; j < IndSet[child][whichBigger].size(); j++) {
IndSet[node][0].push_back(IndSet[child][whichBigger][j]);
}
// include root node -> not use child -> use `dp[child][0]`
dp[node][1] += dp[child][0];
for (int j = 0; j < IndSet[child][0].size(); j++) {
IndSet[node][1].push_back(IndSet[child][0][j]);
}
}
}
travel(int node, int par) 함수는 dp[node][]의 값을 결정하는 함수로 자식 노드들의 dp 값을 순회한다. 문제에서 독립집합에 속하는 원소의 목록을 제시하라는 조건이 있어 IndSet으로 이를 기록하였다.
dp[node][]의 값을 갱신할 때는 두 가지 경우가 있는데,
1. node를 포함하지 않는 경우; dp[node][0]
이 경우 dp[child][0]과 dp[child][1] 중 더 큰 값을 선택하면 된다. 처음 코드를 짤 때는 dp[child][1]를 선택하도록 했는데, 이것은 child 노드를 반드시 선택하게 한다. 그러나 child 선택하는 것이 가중합을 최대로 한다는 보장이 없기 때문에 dp[child][0]과 dp[child][1]의 값을 비교하여 더 큰 값을 선택해줘야 한다!
2. node를 포함하는 경우; dp[node][1]
이 경우는 간단하게 dp[child][0]의 값을 더해주면 된다. 😉
위와 같이 코드를 짜면 문제를 해결할 수 있다.
(참고로 본인은 마지막에 sorting 조건을 잊어서 몇번을 실패했었다… 🤯)
“트리의 독립집합” 문제의 경우 포스트를 작성하면서 다시 풀어보았는데, 확실히 저번에 비해 코딩 스타일이 많이 다듬어졌다. 👍
