Machine Learning Basics

“Machine Learning”을 공부하면서 개인적인 용도로 정리한 포스트입니다. 지적은 언제나 환영입니다 :)

---

Definition. basis function; 기저 함수

$y(\mathbf{x}, \mathbf{w}) = \mathbf{w} \cdot \mathbf{x}$인 Linear Regression식에 input $\mathbf{x}$를 transform 하는 함수를 말함.

\[y(\mathbf{x}, \mathbf{w}) = \mathbf{w} \cdot \phi(\mathbf{x})\]

이런 basis function 여러 개를 사용해 Linear Regression¹ 할 수도 있다.

\[y(\mathbf{x}, \mathbf{w}) = \sum_{j=1}^{M} \mathbf{w}_j \cdot \phi_j(\mathbf{x})\]

Example. basis function

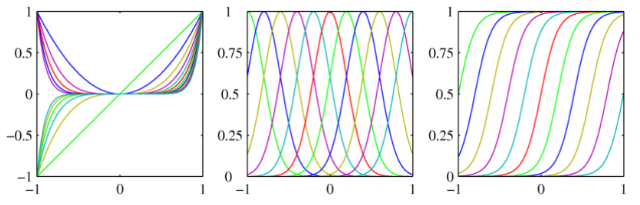
• polynomial basis function

\[\phi_j(x) = (x)^j\]

• sigmoid basis function

\[\begin{aligned} \phi_j(x) = \sigma \left( \frac{x - u_j}{s}\right) \\ \sigma(a) = 1 / (1 + \exp (-a)) \end{aligned}\]

• gaussian basis function

\[\phi_j(x) = \exp \left( - \frac{(x - u_j)^2}{2s^2}\right)\]

---

references

• PRML - Ch.3

---

1. $x$에 대해서는 비선형 함수이지만, $w$에 대해서 선형이므로 Linear Regression이라고 부른다. ↩