Huffman Encoding
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
아쉽게도 <Huffman Encoding>에 대한 백준 문제를 찾지 못 했다. 그래서 자체적으로 문제와 테스트 케이스를 간단하게 만들어 이것을 기준으로 문서를 작성하도록 하겠다 🙏
Situation
Consider a string consisting of 130 million characters and the alphabet {A, B, C, D}. CDABDBACCDDBBCCDCC... How to write this long string in binary with most economic way?
* Input
$1 \le N \le 20$ length alphabetical string.
* Output
Most economic binary encoding.
* Testcase 1
# input
AAAABBBCCD
# output
0000101010111111110
* Testcase 2
# input
ABBCCCBBA
# output
10001111110010
※ NOTE: Several optimal encodings may exist.
사실 아래의 사이트에서 몇가지 테스트케이스를 직접 만들어서 확인할 수 있다.
<Huffman Encoding>은 문자열을 압축하는 대표적인 인코딩 방식이다. 가변 길이 인코딩(variable-length encoding) 방식인데 각 문자의 출현 빈도에 따라 자주 출현하는 문자라면 더 짧은 코드를 부여한다.
고정 길이 인코딩 방식과 가변 길이 인코딩 방식을 한번 비교해보자.
1. 고정 길이 인코딩
A = 00, B = 01, C = 10, D = 11
AAAABBBCCD -> 0000 0000 0101 0110 1011 (20 bits)
2. 가변 길이 인코딩
A = 0, B = 10, C = 111, D = 110
AAAABBBCCD -> 0000 1010 1011 1111 110 (19 bits)
에… 사실 위의 예제에서는 그렇게 많이 줄지 않았지만, 만약 특정 문자의 출현 빈도가 다른 문자보다 압도적으로 많다면 가변 길이 인코딩은 좋은 선택이 될 수 있다! (예를 들어 영어에서는 모음에 해당하는 a, i, u, e, o 문자가 자주 등장할 것이다.)
그러나 이런 <가변 길이 인코딩> 방식은 encoding-decoding이 유일(unique)해야 한다는 조건을 만족해야 한다! 우리가 암호화(encoding) 했지만 정확히 복호화(decoding)하지 못한다면 그것은 전혀 도움이 되지 않는다. <Huffman Encoding>에서는 이를 해결하기 위해 prefix-free 방식으로 문자를 인코딩 한다. 이것은 어떤 인코딩 코드라도 다른 인코드의 prefix가 되지 않는다는 말이다. 예를 들어 A를 101으로 인코딩 했다면, 1, 10, 101로는 절대 인코딩 하지 않는다는 규칙이다.
<Huffman Encoding>은 아래와 같은 알고리즘으로 최적의 인코딩 방식을 찾는다.
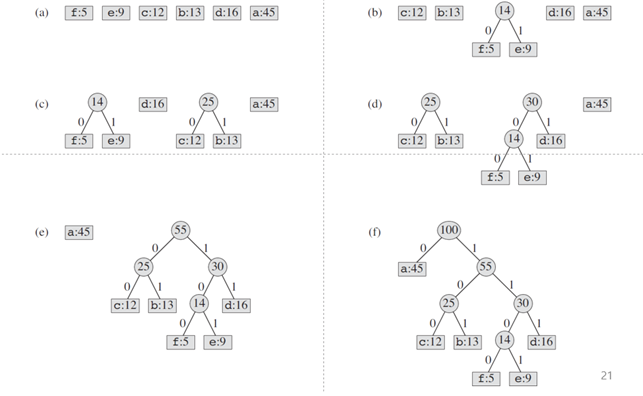
1. 문자열에서 문자들의 빈도수를 계산한다: $\{f_i \mid i \in \Omega \}$
2. 빈도수 $f_i$를 기준으로 문자 집합을 정렬한다.
3. 정렬된 문자 배열에서 가장 작은 빈도를 가지는 2개 문자를 꺼내 각각을 left child, right child로 갖는 트리를 생성한다. 그리고 두 트리의 빈도수를 합친 노드를 다시 문자 배열에 삽입한다.
4. [2-3] 과정을 문자 배열에 단 하나의 노드만 남을 때까지 반복한다.
위와 같은 알고리즘을 구현하기 위해 <우선순위 큐>를 사용한다. 이 자료구조를 사용하면 [2] 과정의 정렬을 직접 수행하지 않아도 된다! 그래서 알고리즘을 다시 쓰면,
1. 문자열에서 문자들의 빈도수를 계산한다: $\{f_i \mid i \in \Omega \}$
2. insert all $f_i$ into a priority queue $H$
3. repeat this until there left one node in $H$
3-1. $u = \texttt{deletemin}(H)$, $v = \texttt{deletemin}(H)$
3-2. create a node $k$ with children $u$ and $v$ and $f_k = f_u + f_v$
3-3. insert new node into $H$
구현
<Huffman Encoding>을 C++로 구현해보자!
문자열을 입력받고, 빈도 수에 대한 Map은 아래와 같이 만들 수 있다.
string ss;
cin >> ss; // Assumption. only uppercase Alphabet
// generate frequency map
map<char, int> freq_map;
for (int i = 0; i < ss.length(); i++) {
if (freq_map[ss[i]]) {
freq_map[ss[i]] += 1;
} else {
freq_map[ss[i]] = 1;
}
}
다음은 Priority Queue $H$에 노드를 넣는 것인데, 그 전에 Node 자료구조를 직접 정의해야 한다.
struct Node {
int freq;
char character;
Node *left;
Node *right;
};
그리고 PQ $H$에 쓰기 위해 비교연산자도 직접 구현해준다.
struct Node_greater {
bool operator()(const Node *left, const Node *right) {
return left->freq > right->freq;
}
};
그리고 PQ $H$를 생성하면,
// insert all nodes into priority queue
priority_queue<Node *, vector<Node *>, Node_greater> pq;
for (auto &freq_pair: freq_map) {
char character = freq_pair.first;
int freq = freq_pair.second;
Node *node = new Node({freq, character, NULL, NULL});
pq.push(node);
}
처음에는 priorirty_queue<Node, ...>로 구현했는데 주소 할당에서 뭔가 꼬이는 느낌이 있어서 동작 할당과 priority_queue<Node *, ...>를 쓰는 방향으로 구현했다.
다음은 PQ $H$에서 노드를 2개씩 꺼내서 Huffman Tree를 생성하면 된다.
// generate Huffman tree
while (pq.size() > 1) {
Node *node1 = pq.top();
pq.pop();
Node *node2 = pq.top();
pq.pop();
Node *newNode = new Node({node1->freq + node2->freq, '0', node1, node2});
pq.push(newNode);
}
그러나 실제로 문자를 인코딩 하기 위해선 위의 과정으로 얻은 PQ $H$에 저장된 마지막 노드인 root 노드를 사용해 Huffman Tree를 순회해야 한다. 이것은 DFS로 아래와 같이 구현할 수 있다.
void dfs(map<char, string> &encode_map, const Node &node, string encode) {
if (!node.left && !node.right) {
encode_map[node.character] = encode;
} else {
dfs(encode_map, *node.left, encode + "0");
dfs(encode_map, *node.right, encode + "1");
}
}
...
// encoding using Huffman tree!
Node *root = pq.top();
map<char, string> encode_map;
dfs(encode_map, *root, "");
for (auto &encode: encode_map) {
cout << encode.first << ": " << encode.second << "\n";
}
위와 같이 잘 구현하면 결과는 아래와 같다.
# Testcase 1
(A 4) (B 3) (C 2) (D 1)
A: 0
B: 10
C: 111
D: 110
# Testcase 2
ABBCCCBBA
(A 2) (B 4) (C 3)
A: 10
B: 0
C: 11
본 포스트는 <Greedy Algorithm> 시리즈의 일부 입니다. 더 많은 <Greedy Algorithm>에 대해 살펴보고 싶다면 아래에서 확인할 수 있습니다 😁
