Quick Selection

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

들어가며

임의의 숫자 배열이 있을 때 $k$번째로 작은 값을 찾는 것을 “Selection”이라고 한다. 쉽게 생각하면 배열을 정렬한 후에 $k$번째 값을 선택하면 되지만, 퀵 정렬을 쓴다면 평균 $O(n \log n)$ 최악의 경우 $O(n^2)$의 비용이 든다. 이번에 다룰 알고리즘은 “정렬되지 않은 배열”에서 $k$번째로 작은/큰 값을 빠르게 찾는 “Quick Selection”이다. “Quick Selection”은 $O(n)$의 비용으로 $k$번재 값을 찾을 수 있다!

Idea

“Quick Selection”의 아이디어는 퀵 정렬과 정말 비슷하다! “Quick Selection”도 pivot을 고르고 left, center, right로 배열을 분할한다.

• input: a list $S$ of numbers and an integer $k$
• output: The $k$-th smallest elt in $S$

Choose a number $v$ from $S$, split $S$ into 3 sublists w.r.t. $v$.

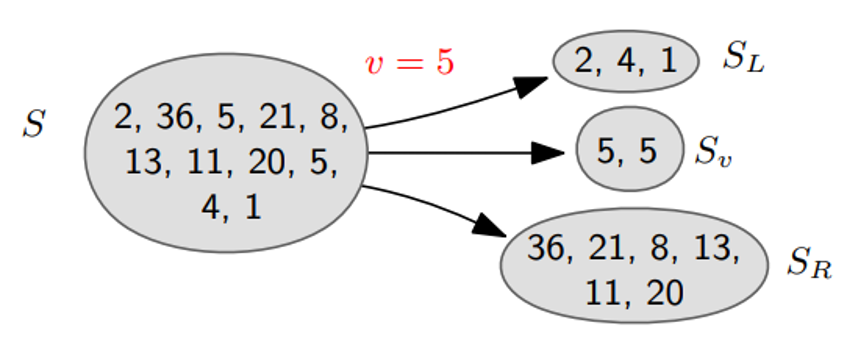
이제 $S_L$, $S_v$, $S_R$의 크기를 기준으로 재귀 함수를 호출한다.

\[\text{selection}(S, k) = \begin{cases} \text{selection}(S_L, k) & \text{if} \quad k \le \left|S_L\right| \\ v & \text{if} \quad \left| S_L \right| < k \le \left|S_L\right| + \left|S_v\right| \\ \text{selection}(S_R, k - \left|S_L\right| -\left|S_v\right| ) & \text{if} \quad k > \left|S_L\right| + \left|S_v\right| \\ \end{cases}\]

“Quick Selection” 알고리즘은 간단하지만 강력하다 👏

How to set pivot

“Quick Selection”의 주요한 이슈는 기준이 되는 $v$ 값을 어떻게 잡느냐 이다. 만약 매 과정마다 $v$를 the smallest elt로 잡으면 최악의 케이스로 $O(n^2)$의 비용이 들게 된다.

\[T(n) = T(n-1) + O(n) = O(n^2)\]

사실 좋은 pivot을 잡기 위한 더 많은 고찰들이 있지만 이번 포스트에서는 “Quick Selection”의 아이디어만 간단히 설명하고 넘어가도록 하겠다. pivot을 잘 잡게 되면 $O(n)$의 비용이 됨을 증명할 수 있다. 아래의 아티클에서 이 내용을 잘 다루고 있으니 더 궁금한 사람들에게 추천한다.

👉 Quick Selection 알고리즘
👉 Median of Medians 알고리즘

Implementation

리트코드의 215. Kth Largest Element in an Array 문제를 통해 해당 문제를 풀어볼 수 있습니다.

class Solution:
    def findKthLargest(self, nums: List[int], k: int) -> int:
        # print(sorted(nums))
        mid = len(nums) // 2
        pivot = nums[mid]

        less_list = []
        same_list = []
        more_list = []
        for num in nums:
            if pivot == num:
                same_list.append(num)
            elif pivot < num:
                more_list.append(num)
            else:
                less_list.append(num)

        if len(more_list) >= k:
            return self.findKthLargest(more_list, k)
        elif k <= (len(more_list) + len(same_list)):
            return pivot
        else:
            return self.findKthLargest(less_list, k - (len(more_list) + len(same_list)))

참고로 C++에서는 “Quick Selection”을 구현할 필요없이 nth_element() 함수를 사용하면 된다 🙌