Closest pair of points

2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.

백준 2261번: 가장 가까운 두 점 문제를 기준으로 작성된 포스트입니다.

---

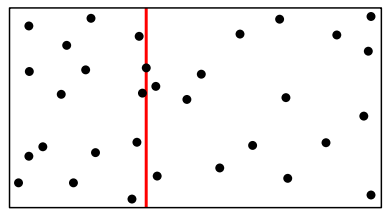
<closest pair of points> 문제는 $n$개의 점이 있는 평면에서 가장 가까운 유클리드 거리를 찾는 알고리즘이다. 이 문제는 공항 관제탑에서 두 비행기가 충돌할지를 확인하고 자동으로 알려주는 시스템 등에서 빠르게 경보를 울리기 위해 필요한 알고리즘이다.

Brute Force 하게 접근한다면 모든 두 점의 쌍에 대해 거리를 구해 최소 거리를 찾을 수 있다. 그러나 이 방법은 $O(n^2)$의 비용을 필요로 한다. 우리는 Divide and Conquer로 접근해 $O(n \log n)$의 비용으로 이 문제를 해결할 것이다! 🙌

1. Sort points in $P$ by $x$-coordinates: $P_x$. And calculate $x$-median $x_{\text{mid}}$

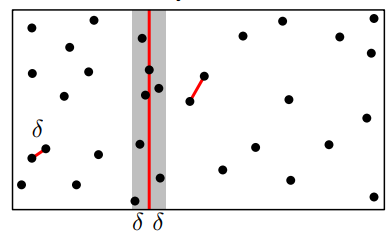
2. Divide the point set $P$ into two equal-sized subsets $P^{L}$ and $P^{R}$ along $x_{\text{mid}}$. And then solve the problem(= find the closest pair in subsets) for two subsets respectively.

3. Choose the minimum of the tow smallest distances, returned from each subproblem: denote it as $\delta$.

4. 아래에서 계속…

delta $\delta$를 구했다면, 이제는 $P^L$, $P^R$에 걸쳐서 존재하는 거리들을 살펴봐야 한다. 이는 $x_{\text{mid}}$에서 좌우로 $\delta$ 만큼의 거리에 있는 점들을 살펴보면 된다. $2\delta$ 길이 만큼의 회색 띠에 속하는 점들은 $O(n)$의 비용으로 쉽게 구할 수 있다. 회색 띠에 속하는 점들을 모두 구했다면 이번에는 $y$-coordinate를 기준으로 정렬한 $P_y$를 유도한다.

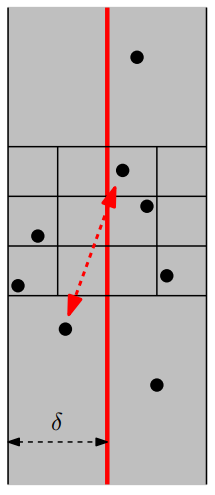
회색 띠 내부를 $\delta/2$ 길이 만큼의 cell로 분할하자. 그리고 $s_i$를 $P_y$에서 $i$번째로 작은 $y$ 좌표를 갖는 점이라고 하자. 그러면 아래의 회색 띠의 cell에 대해 아래 문장이 성립한다!

• No two points lie in same $\delta/2 \times \delta/2$ box.
  • 만약 그런 점이 존재한다면 subproblem을 해결하는 과정에서 $\le \delta/2$가 최소 거리로 뽑혔어야 한다.
• Two points at least 2 rows apart have distance $\ge \delta$.
  • 당연!
• If $\left| i - j \right| \ge 12$, then the distance between $s_i$ and $s_j$ is at least $\delta$.
  • 이것은 1, 2번째 문장으로 유도되는 건데 $i$를 기준으로 12개의 cell을 지나면 길이가 무조건 $\delta$보다 커진다는 말이다.

위의 문장들, 특히 3번 문장으로 인해 우리는 $P_y$에 속한 각 점 $s_i$에 대해 $s_{i+1}$부터 $s_{i+11}$까지 도는 2중 for문을 돌면 회색 띠에서 전체 점 쌍을 확인할 필요 없이 $O(12 n)$의 비용으로 smallest distance를 찾을 수 있다!

시간 복잡도를 분석해보면

• 제일 처음에 들인 point sort: $O(n \log n)$
• 분할 정복: $T(n) \le 2 T(n/2) + O(n) \implies T(n) = O(n \log n)$

로 $O(n \log n)$의 비용으로 문제를 해결할 수 있다!!

---

Code Implementation

알고리즘이 복잡하기 때문에 코드도 조금 복잡하다.

#define Point pair<int, int>
#define point_vec vector<Point>

point_vec points;

long long dist(Point p1, Point p2){
    return (p1.first - p2.first)*(p1.first - p2.first) + (p1.second - p2.second)*(p1.second - p2.second);
}

코드 작성의 편의를 위해 Point와 point_vec 타입을 선언하고, 포인트 거리 함수 dist를 정의한다. 제곱근까지 구할 필요는 없다.

// 콘솔 입력
...
sort(points.begin(), points.end());

printf("%lld", ClosestPair(points));

값을 입력 받은 후에는 $x$값에 따라 point 배열을 정렬한다.

long long ClosestPair(point_vec Px){
    // base case
    if(Px.size() == 2)
        return dist(Px[0], Px[1]);
    if(Px.size() == 3)
        return min({dist(Px[0], Px[1]), dist(Px[0], Px[2]), dist(Px[1], Px[2])});

    int N = Px.size();

    /* divide */
    int mid = N / 2;

    /* Px_L, Px_R */
    point_vec Px_L = point_vec(Px.begin(), Px.begin() + mid);
    point_vec Px_R = point_vec(Px.begin() + mid, Px.end());

    long long d1 = ClosestPair(Px_L);
    long long d2 = ClosestPair(Px_R);
    long long d = min(d1, d2);

    ....
}

몇가지 베이스 케이스들을 처리하고, 포인트 집합 $P_x$를 분할하여 문제를 해결한다. 각각에서 얻은 d1, d2에서의 최솟값을 d에 저장한다.

  /* merge */
  Point point_mid = Px[mid];
  point_vec Sy;
  long long sqrt_d = sqrt(d);
  for(int i = mid; i >= 0; i--){
      if(abs(point_mid.first - Px[i].first) <= sqrt_d)
          Sy.push_back(Px[i]);
      else
          break;
  }
  for(int i = mid + 1; i < N; i++){
      if(abs(point_mid.first - Px[i].first) <= sqrt_d)
          Sy.push_back(Px[i]);
      else
          break;
  }

다음은 가운데의 회색 띠에 속하는 점들 $S_y$ 찾는 작업이다. $O(n)$의 비용이 든다.

  bool yComparator(Point p1, Point p2){
      return p1.second < p2.second;
  }
  ...
  /* sort points in increasing y coordinate */
  sort(Sy.begin(), Sy.end(), yComparator);

  int CrossN = Sy.size();
  for(int i = 0; i < CrossN; i++){
      for(int j = i + 1; j < min(CrossN, i + 12); j++){
          d = min(d, dist(Sy[i], Sy[j]));
      }
  }

  return d;

$S_y$의 점들을 $y$-좌표를 기준으로 정렬한다. 그냥 정렬하게 되면 $x$-좌표를 기준으로 정렬하게 되므로 Comparator를 정의해서 인자로 넣어준다. 그 후에는 $S_y$에 속하는 점들을 순회하며 뒤의 12개의 점들과의 거리를 잰다. $O(n * 12)$의 비용이 든다.

---

<closest pair of points>를 마지막으로 정규 수업에서 다룬 모든 분할 정복의 문제들을 살펴보았다 👏