Linear Programming
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
Introduction to Linear Programming
지금까지 다룬 많은 알고리즘 문제들은 대부분 최적화 문제였다: shortest path, cheapest spanning tree, … 이런 최적화 문제는 대게 2가지로 구성되어 있는데,
- certain constraints
- some criterion 또는 objective function
예를 들어 shortest path를 찾는 문제에서는 제약 조건이 “path는 그래프의 edge만을 사용해야 한다. $s$에서 출발해 $t$에 도착한다”가 된다. 그리고 최적화의 목표는 “제약 조건을 만족하는 가장 짧은 path”를 찾는 것이다.
이번 챕터에서 다루는 <Linear Programming>은 많은 종류의 최적화 문제를 포괄하는 개념인데, <Linear Programming>은 제약 조건(constraint)와 목표(objective function)이 모두 linear function이다!
이번 포스트에서는 어떤 문제들이 <Linear Programming>에 속하는지 그리고 그 문제들을 어떻게 <Linear Programming>의 형식으로 표현할 수 있는지를 살펴본다.
Profit Maximization
A, B 두 개의 상품을 제조하는 회사가 있다고 하자. 회사는 아래와 같이 조건에서 두 상품을 생산할 수 있다고 한다.
A 상품: $1 profit per piece, $\le 200$ pieces demand per day
B 상품: $6 profit per piece, $\le 300$ pieces demand per day
그리고 회사의 노동력은 아래와 같다.
노동력: produce $\le 400$ pieces per day
가장 많은 이윤을 벌기 위해선 노동력을 어떻게 분배해야 할까?
이 문제는 중고등학교 수학 시간에 배울 정도로 쉬운 문제이다. 이걸 <Linear Programming; 이하 LP>의 형식으로 표현해보자.
Variables
- $x_1$: # of item A to produce per day
- $x_2$: # of item B to produce per day
Constraints
- $x_1, x_2 \ge 0$
- $x_1 \le 200$ and $x_2 \le 300$
- $x_1 + x_2 \le 400$
Objective Function
maximize project per day: $\max \; (x_1 + 6 x_2)$
문제를 LP의 형식으로 표현했으면 이제 문제를 해결해보자. 가장 먼저 할 일은 Constraint를 인식하는 것이다.
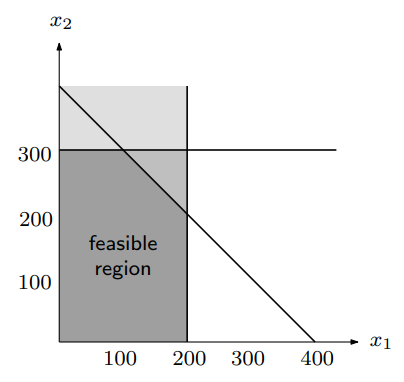
이 위에 objective function을 표현하면 아래와 같다.
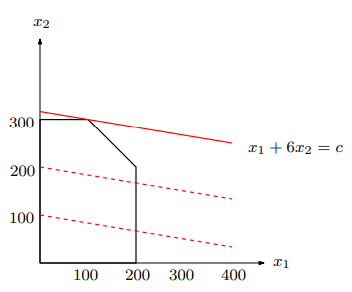
결국 constraints가 유도하는 feasible region 중에서 max. profit을 얻을 수 있다! 👏
Diet Problem
다른 종류의 음식 $n$개 있다: $F_1, …, F_n$. 그리고 각 음식은 $m$ 종류 만큼의 영양소를 함유하고 있다: $N_1, …, N_m$.
또 식단과 관련해 아래의 요소들이 있는데,
- $a_ij$를 음식 $F_i$ 하나에 있는 영양소 $N_j$의 양이라고 하자.
- $r_j$를 하루에 섭취해야 하는 영양소 $N_j$의 양이라고 하자.
- $x_i$를 하루에 섭취하는 음식 $F_i$의 양이라고 하자.
- $p_i$를 음식 $F_i$의 하나의 가격이라고 하자.
하루 식단은 음식 조합을 어떻게 하느냐에 따라 달렸다. 우리는 가장 적은 비용으로 적절한 영양을 섭취하는 식단을 짜야 한다.
생활에 밀접한 식단 문제이다. 이걸 LP 형태로 표현해보자.
Variables
- $x$: $n$차원 벡터로 음식 $F_i$의 양을 의미한다.
Objective Function
minimize cost: $p_1x_1 + p_2x_2 + \cdots + p_nx_n$
Constraints
- $x_i \ge 0$
- $a_{1j}x_1 + a_{2j}x_2 + \cdots + a_{nj}x_n \ge r_j$
Assignment Problem
$n$명의 직원과 $m$개의 작업이 있다. 직원 $i$가 작업 $j$를 하루 종일 할 때의 효용이 $a_{ij}$라고 하자. 그러나 하나의 작업을 수행할 때는 한 명의 사람이 배정되어야 하고, 각 직원은 하루를 쪼개서 하루에 여러 개의 일을 수행할 수 있다. 우리는 직원들에게 하루치 작업을 적절히 분배해서 최고의 효용의 달성하고자 한다.
Variables
- $x_{ij}$: 직원 $i$가 작업 $j$에 하루를 쓰는 비율
Constraints
- $0 \le x_{ij} \le 1$
- \(\displaystyle \sum^{m}_{j=1} x_{ij} \le 1\): 직원 $i$는 하루 이상의 시간을 쓸 수는 없다.
- \(\displaystyle \sum^{n}_{i=1} x_{ij} \le 1\): 작업 $j$에 하루 치 이상의 작업을 하도록 할당할 수는 없다.
Objective Function
maximize \(\displaystyle \sum^{n}_{i=1} \sum^{m}_{j=1} a_{ij} x_{ij}\)
Production Planning
도자기를 만드는 공장이 있다. 그 공장에 들어오는 월간 주문은 대략 $440 \le d_i \le 920$ 정도라고 한다. 공장에는 현재 30명의 직원이 있다. 직원들은 한달에 20개의 도자기를 만들 수 있으며, 2000원의 월급을 받는다.
공장은 직원을 추가로 고용하거나 해고할 수 있는데, 각각 320원과 400원의 비용이 든다.
…
문제가 좀 길어서 일단 여기까지 읽고 LP 형태로 기술해보자.
Variables
- $w_i$: $i$번째 달에 고용된 직원 수, 처음에는 30명의 직원이 있다. $w_0 = 30$
- $x_i$: $i$번째 달에 생산한 도자기의 수
- $h_i, f_i$: $i$번째 달에 고용하거나 해고한 직원의 수
Constraints
- $w_i, x_i, h_i, f_i \ge 0$
- $x_i = 20 w_i$
- $w_i = w_{i-1} + h_i - f_i$
Objective Function
아직 문제에는 안 나왔지만, 결국은 공장 운영 비용을 최소화하는 문제다.
\[\min \quad 2000 \sum_i w_i + 320 \sum_i h_i + 400 \sum_i f_i\]문제를 계속 읽어보자.
…
초과근무를 통해 도자기를 추가로 생산할 수 있다. 이때 생산된 도자기는 기존 급여의 80%를 초과근무 비용으로 지불해야 한다. 초과근무는 능률이 떨어지기 때문에 직원 한명이 초과 근무로 생산하는 도자기 수도 6개 뿐이다.
…
Variables
- $o_i$: $i$번째 달에 초과근무로 생산된 도자기의 수
Constraints
- $o_i = 6 w_i$
- $x_i = 20 w_i + o_i$
Objective Function
도자기 하나에 $2000/20 = 100$을 급여로 제공했다. 초과근무로 생산된 것에 대해선 80%를 더 주기로 했으니 초과근무로 생상된 도자기 하나에 $180$의 초과근무 급여를 제공해야 한다.
\[\min \quad 2000 \sum_i w_i + 320 \sum_i h_i + 400 \sum_i f_i + 180 \sum_i o_i\]…
공장은 매달 말에 여분의 도자기를 저장할 수 있다. 도자기를 저장하는데 8의 비용이 들며, 년도의 시작과 끝에는 저장하는 도자기가 없다.
Variables
- $si$: $i$번째 월말에 저장할 도자기 수, $s_0 = 0$
Constraints
- $s_i = s_{i-1} + x_i - d_i$
Objective Function
\[\min \quad 2000 \sum_i w_i + 320 \sum_i h_i + 400 \sum_i f_i + 180 \sum_i o_i + 8 \sum_i s_i\]Bandwidth Allocation
네트워크 공급자는 아래와 같은 조건으로 네트워크를 구축하려고 한다.
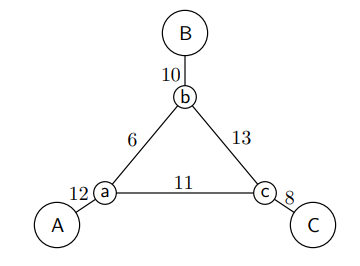
- 데이터 전송 단위 당 A-B 연결에서는 3의 수익이, B-C 연결에서는 2의 수익이, A-C 연결에서는 4의 수익이 난다.
- 즉, A-B에서 1 유닛 만큼 정보를 주고 받으면 3만큼의 이득이 난다는 것이다.
- 각 연결은 2 이상의 단위 유닛 만큼 정보를 주고 받는다.
- 각 연결은 long path과 short path 또는 복합적인 형태로 형성된다.
위와 같은 연결 형태를 이용해 네트워크 이윤을 최대화 하도록 네트워크 라우팅을 구성하라.
Variables
- $x_{AB}$: short-path bandwidth allocated to the connection btw $A$ and $B$
- $x’_{AB}$ long-path bandwidth allocated to the connection btw $A$ and $B$
Objective Function
\[\max \; 3 x_{AB} + 3 x'_{AB} + 2 x_{BC} + 2 x'_{BC} + 4 x_{CA} + 4 x'_{CA}\]Constraints
\[x_{AB}, x'_{AB}, x_{BC}, x'_{BC}, x_{CA}, x'_{CA} \ge 0\] \[\begin{aligned} x_{AB} + x'_{AB} &\le 2 \\ x_{BC} + x'_{BC} &\le 2 \\ x_{CA} + x'_{CA} &\le 2 \end{aligned}\] \[\begin{aligned} x_{AB} + x'_{AB} + x_{BC} + x'_{BC} &\le 10 & [\text{edge}(b, B)] \\ x_{AB} + x'_{AB} + x_{CA} + x'_{CA} &\le 12 & [\text{edge}(a, A)] \\ x_{BC} + x'_{BC} + x_{CA} + x'_{CA} &\le 8 & [\text{edge}(c, C)] \end{aligned}\] \[\begin{aligned} x_{AB} + x'_{BC} + x'_{CA} &\le 6 & [\text{edge}(a, b)] \\ x_{BC} + x'_{AB} + x'_{CA} &\le 13 & [\text{edge}(b, c)] \\ x_{CA} + x'_{AB} + x'_{BC} &\le 11 & [\text{edge}(c, a)] \end{aligned}\]이것으로 LP의 문제로 표현할 수 있는 예시 사례들을 살펴보았다. 현실의 문제를 LP로 풀기 위한 가장 기본적인 단계는 위와 같이 Variables, Objective Function, Constraints로 정제해서 확인하는 것이다. LP를 푸는 것은 그 다음의 일이다.
다음 포스트에서는 LP 문제를 푸는 방법인 <Simplex Method>에 대해 살펴본다.
