쿼드 트리 뒤집기

‘알고리즘 문제해결 전략’을 읽고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :)

알고스팟 QUADTREE: 쿼드 트리 뒤집기 문제를 다루는 포스트입니다 🙌

---

<쿼드 트리; quad tree>란 대량의 좌표 데이터를 압축하기 위한 기법이다. 2차원 배열을 4개의 공간으로 재귀적으로 분할해 표현하기 때문에 쿼드(quad)라는 이름이 붙었다. 쿼드 트리는 0과 1로 이루어진 흑백 이미지를 압축하는데 사용할 수 있다. $2^N \times 2^N$ 크기의 흑백 그림을 압축하는 규칙은 아래와 같다.

• 그림의 모든 픽셀이 검은 색일 경우, b로 압축할 수 있다.
• 그림의 모든 픽셀이 흰 색일 경우, w로 압축할 수 있다.
• 만약 모든 픽셀이 같은 색이 아니라면, 그림을 가로-세로로 각 2등분하여 4개의 조각을 쪼갠 뒤 각각을 다시 쿼드 트리 압축한다. 압축 결과는 x(LU)(RU)(LD)(RD) 순으로 인코딩 된다.

이 방식으로 (a) 그림을 압축하면, x(x(wwwb)x(wx(wbbb)ww)x(x(x(wwbb)bww)wwb)b)가 된다. 쉽게 구분하기 위해 괄호를 넣었는데 이를 제거하면, xxww wbxw xwbb bwwx xxww bbbw wwwb b가 된다.

흑백 이미지를 쿼드 트리로 인코딩 하는 알고리즘은 재귀로 구현할 수 있다. 백준 1992번: 쿼드트리는 이 쿼드트리 인코딩 알고리즘을 요구하는 문제다. 쉽게 짤 수 있기 때문에 본 포스트에서는 다루지 않겠다.

우리가 해결할 문제는 아래와 같다.

쿼드 트리로 압축된 흑백 그림이 주어졌을 때, 이 그림을 상하로 뒤집은 그림을 쿼드 트리 압축해서 출력하라.

---

Brute Force

가장 단순한 방법은 쿼드트리 인코딩을 디코딩 해 원본 흑백 그림을 얻는다. 이를 상하로 뒤집은 후, 다시 쿼드트리 인코딩 한다. 그러나 이 방법은 매우 큰 흑백 그림은 인코딩 했을 때는 디코딩 했을 때의 이미지가 너무 크기 때문에 적합하지 않다. 문제에서 입력 가능한 원본 그림의 크기는 $2^{20} \times 2^{20}$인데 이는 1 테라바이트에 맞먹는 크기이기 때문에 현실적으로 불가능하다. 그래서 Brute Force 접근은 유효하지 않다.

---

분할정복

종만북에서는 Brute Force 방법이 유효하지 않다는 걸 깨달았을 때, 어떻게 접근해야 할지 아래와 같이 조언한다.

작은 입력에 대해서 동작하는 알고리즘을 구상한다. 그리고 입력을 키워가면 가능한 모든 입력 케이스에서 동작하도록 알고리즘을 보완한다.

이 문제의 경우는 작은 입력이라고 하면, $2^{0} \times 2^{0}$인 그림이다. 이 경우는 w 또는 b 뿐이다. 다음의 경우는 $2^1 \times 2^1$인 그림이다. 이 경우, w이거나 b이거나 xOOOO이다.

w인 경우를 먼저 확인하자. 이것은 4개 조각이 모두 w인 경우다. LU = RU = LD = RD = w인 경우다. b인 경우도 동일하다. 만약 한 조각이라도 다른 그림이 섞여 있다면 xOOOO에 해당한다. 일단 xwwbb를 생각해보자.

w w  ----> b b
b b        w w

이 경우는 간단하게 LU를 LD와 맞바꾸고 RU를 RD와 맞바꾸면 된다. 다른 모든 xOOOO 패턴에서 동일하다!

다음은 $2^2 \times 2^2$이다. w와 b에 대한 판단은 $2^1 \times 2^1$ 때와 동일하게 하면 된다. 일단 LU이 xOOOO이고 나머지는 모두 w라고 생각하자.

w w  w w  ---->  w w  w w  --(정답)-->  w w  w w
b w  w w         w w  w w               w w  w w

w w  w w         w w  w w               b w  w w
w w  w w         b w  w w               w w  w w

이 경우는 위 아래를 맞바꾼다고 해서 쉽게 해결되지 않는다. 여기 부분이 쿼드 트리 뒤집기의 핵심 아이디어다! 단순히 위 아래만 맞바꿀때와 정답을 비교해보면, LD 부분이 다르다. 정확하게는 LD 부분이 상하가 반전되어 있다. 여기서 우리는 LD에 대해 상하 반전, 즉 쿼드트리 뒤집기를 해야 함을 깨닫는다! 👏 즉, 4개 조각에 대해 쿼드트리 뒤집기를 한 후에 상하를 바꿔줘야 한다는 말이다. 결국 쿼드트리 뒤집기를 하기 위해 작은 4개 조각에서 쿼드트리 뒤집기를 해줘야 하는, 즉 재귀 문제를 해결해야 한다는 걸 깨닫는다. 여기까지 했으면 사고 알고리즘은 완성이다!

Implementation

이제 머릿속에 있는 알고리즘을 코드로 구현해보자.

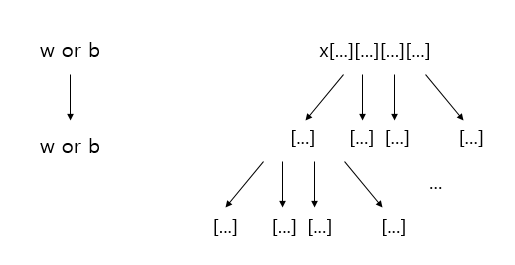
재귀 형태를 간단하게 표현 하면 위와 같다. 그러나 이걸 코드로 구현해보려고 한다면, 입력으로 들어오는 x[...][...][...][...]를 어떻게 [...]로 분할 할지 고민하게 된다. 종만북에서는 getChunkLength()라는 함수를 만들어 어떻게 chunk가 나뉘는지 구해볼 수 있다고 설명한다. 이 함수를 어떻게 구현할까? 일단 접근은 “작은 입력에서” 먼저 생각해보자.

입력을 length 1인 경우에서 가장 기본적인 xOOOO까지 단계적으로 늘려 가다보면 패턴이 눈에 보인다. 이 패턴에 따라 구현해보면,

int getChunkLength(string& tree, int idx) {
  if (tree[idx] == 'w' || tree[idx] == 'b') {
    return 1;
  }

  // x[...][...][...][...]
  int lenSum = 1;
  int nextIdx = idx + 1;
  for (int i = 0; i < 4; i++) {
    if (tree[nextIdx] == 'x') {
      int chunkLen = getChunkLength(tree, nextIdx);
      lenSum += chunkLen;
      nextIdx += chunkLen;
    } else {
      lenSum += 1;
      nextIdx += 1;
    }
  }
  return lenSum;
}

더 예쁘게 짤 수 있었을 텐데… 암튼 이 함수를 이용해 문제를 계속 풀어보자.

string quad_tree(string encoding) {
  if (encoding.size() == 1) {
    return encoding;
  }

  // x[...][...][...][...]
  int nextIdx = 1;

  int LU_len = getChunkLength(encoding, nextIdx);
  string LU = encoding.substr(nextIdx, LU_len);
  string LU_rev = quad_tree(LU);
  nextIdx += LU_len;

  int RU_len = getChunkLength(encoding, nextIdx);
  string RU = encoding.substr(nextIdx, RU_len);
  string RU_rev = quad_tree(RU);
  nextIdx += RU_len;

  int LD_len = getChunkLength(encoding, nextIdx);
  string LD = encoding.substr(nextIdx, LD_len);
  string LD_rev = quad_tree(LD);
  nextIdx += LD_len;

  int RD_len = getChunkLength(encoding, nextIdx);
  string RD = encoding.substr(nextIdx, RD_len);
  string RD_rev = quad_tree(RD);
  nextIdx += RD_len;

  return "x" + LD_rev + RD_rev + LU_rev + RU_rev;
}

int main() {
  string s;
  cin >> s;

  cout << quad_tree(s);
}

본인의 코드는 많이 지저분 하지만 종만북은 getChunkLength() 함수도 없이 iterator를 사용해 훨씬 우아한 코드를 제시했다. 약간 DFS의 느낌으로 트리를 순회하는 접근이었다. 종만북의 코드를 참고하길 추천한다 👏