Branch and Bound
2020-1학기, 대학에서 ‘알고리즘’ 수업을 듣고 공부한 바를 정리한 글입니다. 지적은 언제나 환영입니다 :) 전체 포스트는 Algorithm 포스트에서 확인하실 수 있습니다.
지난번에 살펴본 <Backtracking>과 비슷하게 <Branch-and-Bound> 테크닉 역시 partial solution을 검사해 Search Space를 줄이는 테크닉이다. <Bracktracking>과 전체적인 구조는 완전 동일한데, partial solution을 bound를 사용해 $\text{test}$한다는 구체적인 방법이 명시되어 있다.
대충 어떤 느낌인지 훑고 가자. 만약 우리가 minimization problem을 풀고 있다고 하자. 그리고 partial solution $S_i$를 탐색하고 있다고 하자. 우리는 이 partial solution $S_i$를 더 확장했을 때의 잠재적인 비용을 ‘예상’할 것이다. 구체적인 비용을 구하려고 하는 것이 아니라 ‘예상’이기 때문에 ‘lower bound’를 계산할 것이다. 사례를 보면 좀더 이해가 빠를 것이다. <TSP> 문제를 <Branch-and-Bound>로 해결하는 과정을 살펴보자!
TSP with Branch-and-Bound
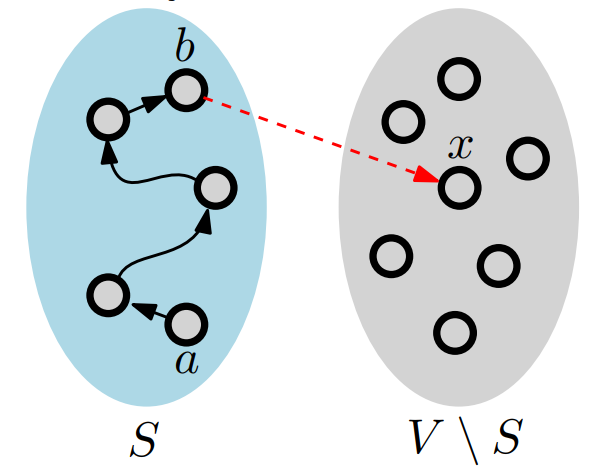
Complete weighted graph $G = (V, E)$를 생각해보자. 우리는 지금 $a$에서 출발해 $b$에 도달하는 partial solution을 가지고 있다. 이 partial solution은 vertex set $S$의 원소들을 정확히 한번씩 지나가는 Hamilton Path다. 이 partial solution을 $[a, S, b]$로 표현하겠다.
partial solution $[a, S, b]$를 확장해보자. 그것은 $S$를 제외한 vertex $x \in V \setminus S$ 중에 하나를 선택해 $(b, x)$ edge를 추가해 해밀턴 경로를 확장하는 것이다. 이렇게 할 경우, 남은 정점 수 $\left| V \setminus S \right|$만큼의 subproblem $[a, S \cup \{ x \}, x]$가 새로 생성된다.
여기까지 <TSP> 문제를 탐색과 subproblem의 관점에서 기술해본 것이다.
우리는 partial solution $[a, S, b]$를 확장하기 전에, 남은 vertex set $V \setminus S$를 통해 TSP의 lower bound를 구할 수 있다! lower bound를 구하는 여러 방법들이 있겠지만, 가장 간단한 방법은 아래 4가지 비용의 합을 lower bound로 삼는 것이다.
- the lightest edge from $a$ to $V \setminus S$
- the lightest edge from $b$ to $V \setminus S$
- the minimum spanning tree of $V \setminus S$
- and current cost of partial solution
각각 모두 $V \setminus S$의 정점으로 partial solution을 확장 했을 때 가능한 가장 최소 수준의 비용이다. 그래프의 MST를 구하는 것은 polynomial-time으로 가능하기에 복잡도에 큰 영향을 주지도 않는다. 따라서 이를 lower bound로 사용하는 것은 적절하다!
좀더 구체적인 예를 통해 익숙해져보자!

위와 같은 Graph에서 TSP 문제를 해결한다고 해보자. 일단 $A$ 노드에서 시작하는 탐색 트리를 확장해가자.
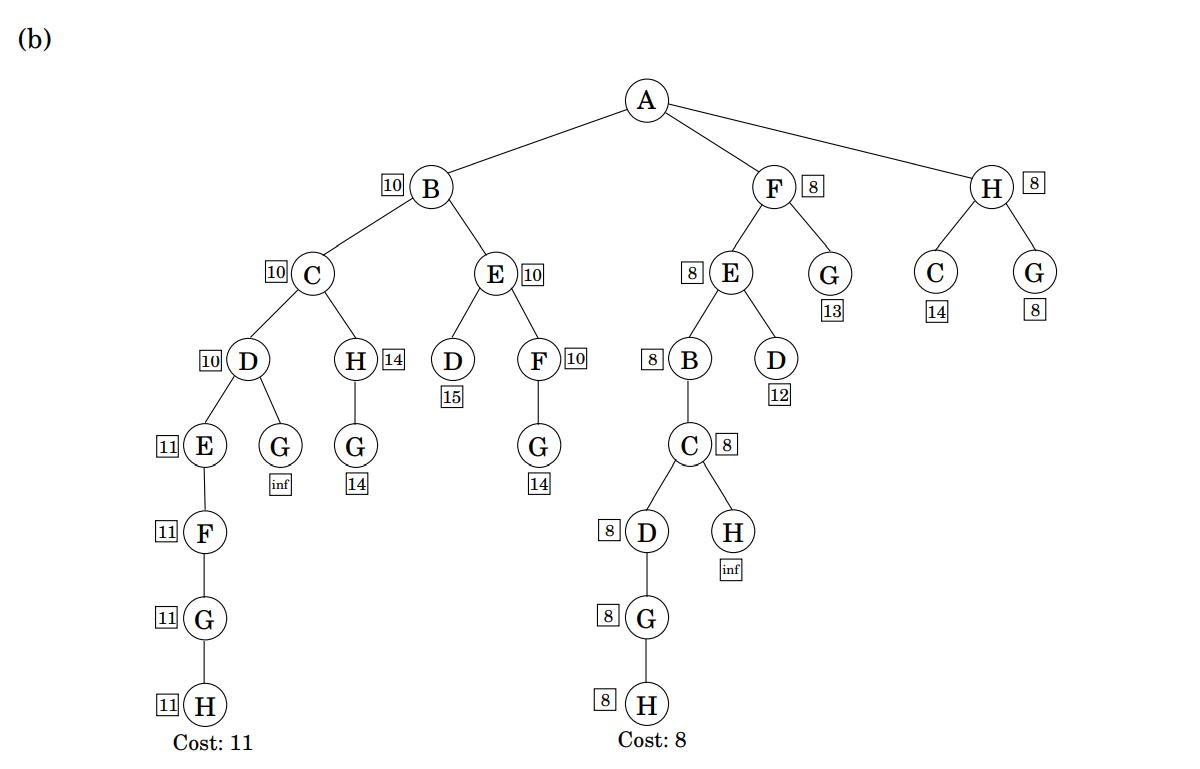
트리 노드 옆의 상자엔 해당 노드의 lower bound가 적혀있다. DFS 방식을 통해 트리를 탐색한다고 하면, 가장 먼저 $H$ 노드로 끝나는 왼쪽 경로를 타게 된다. 이때의 total cost가 11인데, 이것을 $\text{bestsofar}$ 값으로 저장해두고 다음 노드를 선택해 확장해간다.
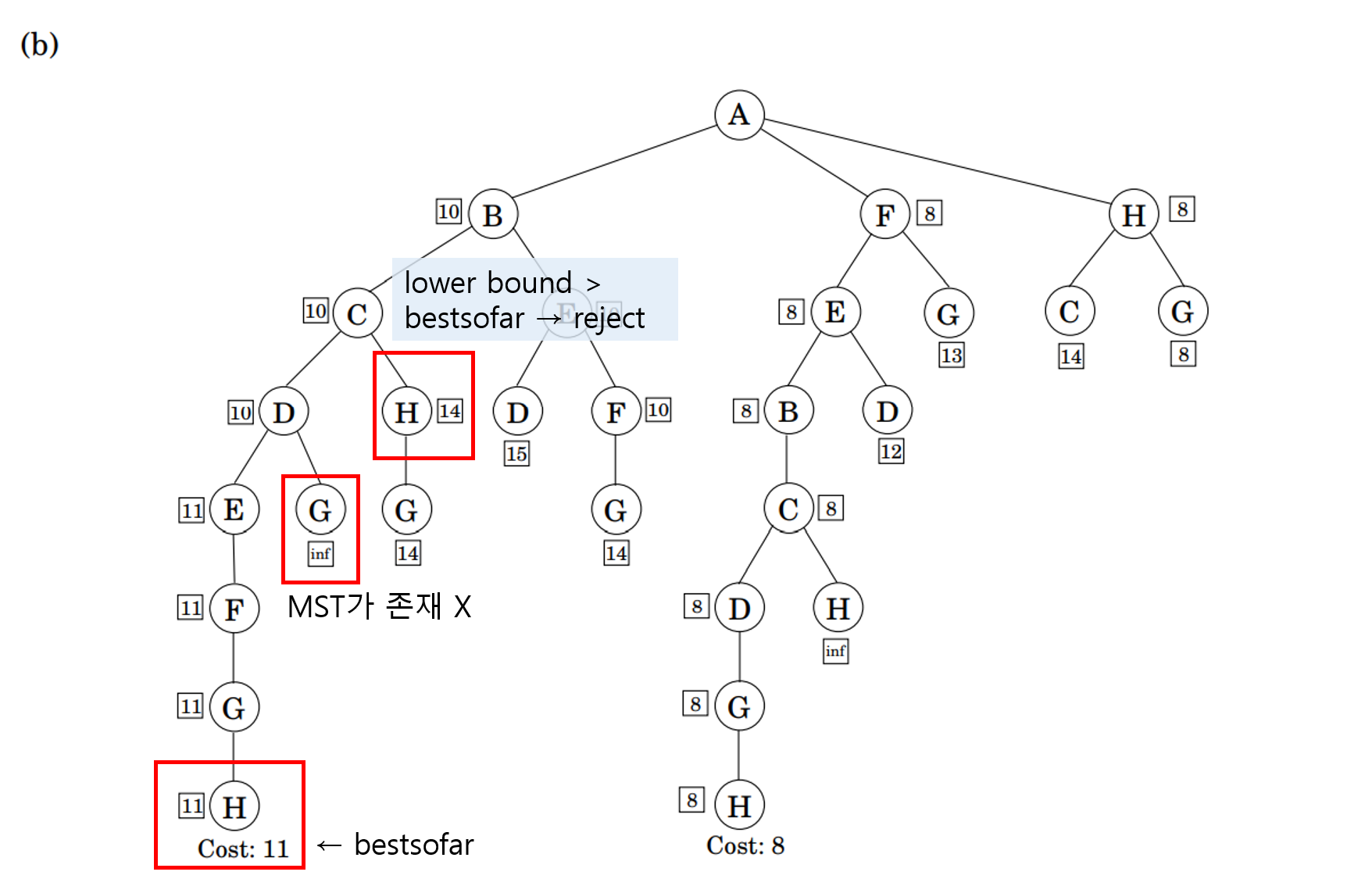
현재 비용 11이 $\text{bestsorfar}$ 값이다. 만약 다음 partial solution을 탐색했을 때, 비용의 lower bound가 $\text{bestsorfar} = 11$보다 크다면 해당 노드는 탐색할 필요가 없다!
이 방법을 활용해 partial solution들을 reject하고 lower bound가 적절히 낮은 partial solution들만 확장해간다. 최종적으로는 $\text{bestsorfar} = 8$을 solution으로 리포트한다.
Overview
To expand a subproblem, its lower bound should be smaller than the bestsofar. Otherwise, it’s clear that the cost of subproblem will exceed the bestsofar, so reject it!
<Branch-and-Bound> 알고리즘의 원리를 요약하면 아래와 같다.
Start with some problem $P_0$
Let $S = \{ P_0 \}$, the set of active subproblems.
Set $\text{bestsofar} = \inf$
while $S$ is non-empty:
choose a subproblem $P \in S$ and remove it from $S$.
expand it into smaller subproblems $P_1, P_2, \dots, P_k$
for each $P_i$:
if $P_i$ is a complete solution: update $\text{bestsofar}$
else: if $\text{lowerbound}(P_i) < \text{bestsofar}$, then add $P_i$ to $S$.
return $\text{bestsofar}$
이전에 살펴본 <Backtracking>과 큰 틀에서 비슷하다! 단지 <Branch-and-Bound>가 $\text{test}(P_i)$를 lower bound로 판단하고 구체적으로 명시되어 있을 뿐이다!
