Partial Correlation
Introduction
Partial Covariance/Correlation는 여러 개의 독립변수(IV)와 하나의 종속변수(DV)가 있는 상황에서 등장하는 개념이다.
우리는 독립변수를 하나를 잡고, 그 녀석과 종속변수의 Covariance를 계산할 수 있다. 만약에 존재하는 독립변수들 사이에 상관관계가 없다면, 상황은 아주 간단하다. 그냥 $\text{Cor}(\text{IV}, \text{DV})$가 가장 높은 독립변수 하나를 찾으면 된다. 또, $r = \text{Cor}(\text{IV}, \text{DV})$는 $\left[-1, +1 \right]$의 부호가 있기 때문에, 제곱해서 얻은 $r^2$ 값으로 그 독립변수의 설명력도 확인할 수 있다.
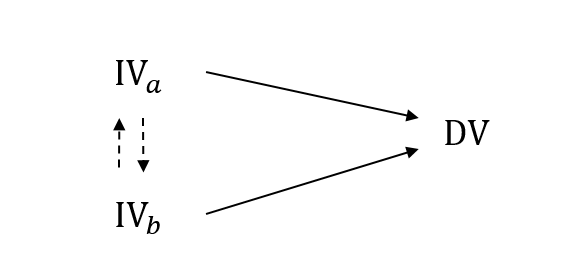
그러나 독립변수들 사이에 상관관계가 있다면, 상황이 복잡해진다. 예를 들어 $\text{IV}_a \rightarrow \text{DV}$라고 해보자. 그런데 다른 독립변수 $\text{IV}_b$에 대해 $\text{IV}_b \rightarrow \text{IV}_a$ 것이 밝혀졌다. 그렇다면, $\text{IV}_a \rightarrow \text{DV}$는 사실 $\text{IV}_b \rightarrow \text{DV}$라고 말할 수 있다.
왜 독립변수 간의 상관성이 문제가 되는가?
독립변수 간의 상관성이 있는 상황은 왜 문제가 되는 걸까?🤔 $\text{Cor}(\text{IV}_a, \text{DV})$의 값을 계산했다고 해보자. 그런데 이것이 $\text{IV}_a$ 단독의 순수한 효과일까? 아니면 $\text{IV}_a$와 상관성이 있는 $\text{IV}_b$의 효과가 일부 반영된 결과일까?
실험자는 독립변수 $\text{IV}_a$ 하나만을 컨트롤 할 수 있어 $\text{IV}_a$ 단독의 영향력을 아는 것이 중요한 상황인 걸 수도 있다. 결국 독립변수 단독의 영향력/설명력을 알고 싶다면, $\text{Cor}(\text{IV}_a, \text{DV})$ 만으로는 부족하다.
단일 독립변수로 Regression Problem을 푸는 상황에서는 독립변수가 하나이니 별 상관이 없지만, 2개 이상의 독립변수가 있는 Multiple Regression Problem에서는 이런 독립변수 단독의 상관성을 아는게 중요하다.
Partial Correlation
Partial Correlation은 다른 변수의 효과를 배제하면서, 두 변수 사이의 Correlation을 측정하는 방법을 제공한다. 이렇게 다른 변수의 효과를 배제하는 것을 “Partialling Out“이라고 한다.
Partial Correlation의 표현과 성질부터 살펴보자.
Partial Correlation은 $\rho$(rho)로 표현한다. 두 랜덤변수 $X$, $Y$에 대해 다른 랜덤변수 $Z$를 배제한 Partial Correlation은 아래와 같이 기술한다.
\[\rho_{XY\cdot Z}\]Partial Correlation도 Correlation과 마찬가지로 $\left[-1, +1\right]$의 범위를 갖는다.
Exercise
간단한 예제를 통해 Partial Corr을 알아보자. 예제는 Statistics 101: Model Building, A Visual Guide to Partial Correlation 영상의 것을 빌려왔다. 🙏
MTCARS라는 유-명한 데이터셋을 사용할 것이다. 요 GitHub 링크에서 데이터를 볼 수 있다. 이 중에서 연비인 MPG(Miles per gallon)를 종속 변수로, DRAT(rear axle gear ratio)과 HP(engine horsepower)를 독립변수로 상관관계 분석을 진행할 것이다.
- 독립변수
- DRAT $X_1$
- HP $X_2$
- 종속변수
- MPG $Y$
3개의 변수에 대해 Correlation Matrix를 그려보면 아래와 같다.
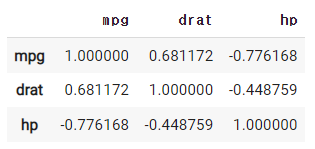
각 변수의 Correlation
해석해보면,
- MPG와 DRAT는
0.68로 높은 상관관계를 보인다. - MPG와 HP는
-0.78로 높은 상관관계를 보인다. - 독립변수인 DRAT과 HP는
-0.45로 약간의 상관관계를 보인다.
Correlation은 +/- 부호를 가지니 제곱한 $r^2$를 사용하자.
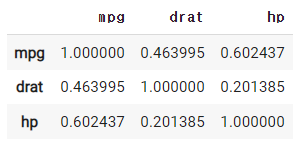
각 변수의 $r^2$
자! 여기서부터 Partial Correlation을 구하는 과정이 본격적으로 시작된다! 👏
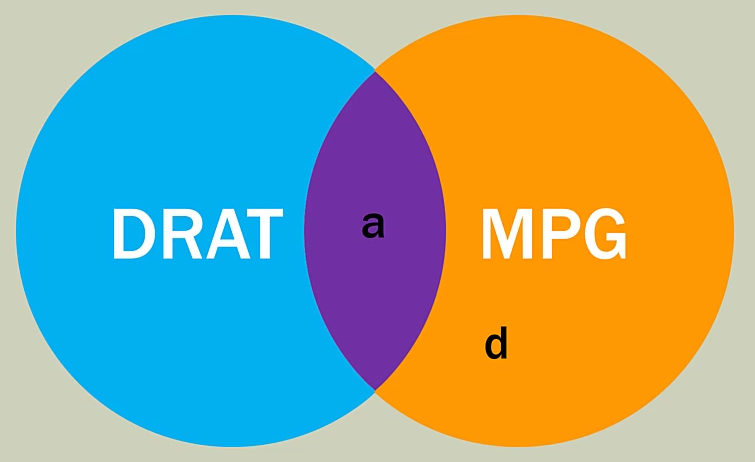
DRAT과 MPG
독립변수 DRAT과 종속변수 MPG의 $r^2$ 값은 0.46이었다. 이것은 DRAT를 통해 MPG를 0.46 만큼 설명할 수 있다는 말이다. 위의 그림에 $a$에 해당하는 영역이 DRAT에 의해 설명되는 MPG의 크기다.
마찬가지로 HP와 MPG도 위와 같은 벤 다이어그램을 그릴 수 있다. DRAT, HP, MPG 3가지를 모두 그리면 아래와 같다.
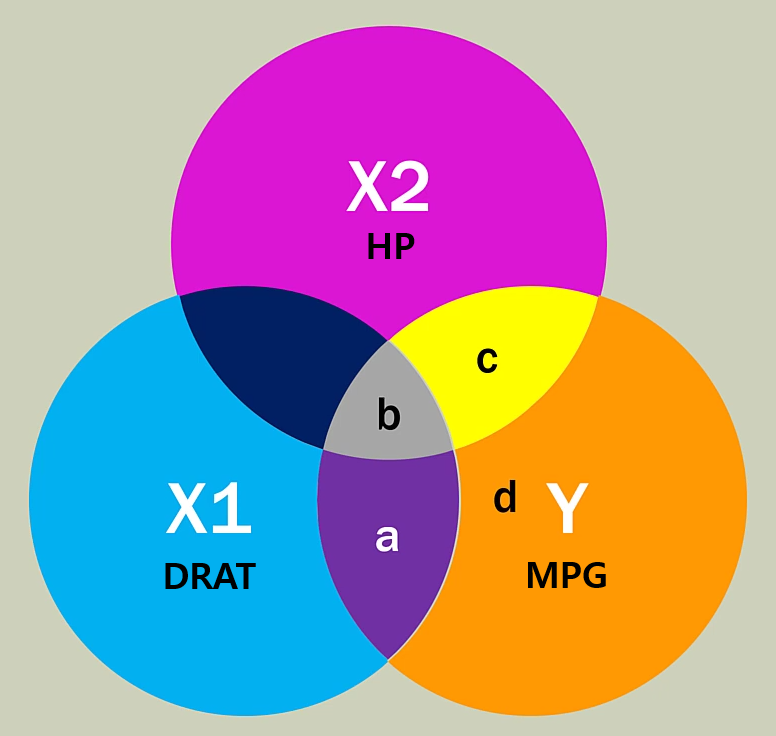
DRAT, HP, MPG
우리가 지금까지 얻은 정보를 정리하면 아래와 같다.
- $a + b + c + d = 1$
- $a + b = 0.46$
- $b + c = 0.60$
그러나 위의 3가지 정보만으로는 개별 요소의 값을 구할 수 없다. 그래서 우리는 DART, HP 두 가지 독립변수로 Multiple Regression을 했을 때의 $R^2$ 값을 사용할 것이다.
Multiple Regression의 $R^2$ 값은 0.74이다.
이를 통해 하나의 수식이 추가되는데, $a + b + c = 0.74$이다.
따라서, $a$, $b$, $c$, $d$의 값을 구하면
- $a = 0.14$
- $b = 0.32$
- $c = 0.28$
- $d = 0.26$
드디어…! 👏 Partial Corr $\rho$를 구해보자!
\[\left(\rho_{X_1 Y \cdot X_2}\right)^2 = \frac{a}{a + d} = \frac{0.14}{0.14 + 0.26} = 0.35\] \[\rho_{X_1 Y \cdot X_2} = \sqrt{0.35} = 0.59\] \[\left(\rho_{X_2 Y \cdot X_1}\right)^2 = \frac{c}{c + d} = \frac{0.28}{0.28 + 0.26} = 0.52\] \[\rho_{X_2 Y \cdot X_1} = - \sqrt{0.26} = -0.72\]몇가지 분수 연산을 거쳐서 드디어! Partial Correlation을 구했다! 👏 Partial Correlation $\rho$를 기존의 Correlation 값과 비교해보자!
| Variable | Corr | Partial Corr |
|---|---|---|
| DRAT | 0.68 | 0.59 |
| HP | -0.77 | -0.72 |
Corr보다 Partial Corr일 때, 상관성의 크기가 더 작아진 것을 확인할 수 있다! 이 사실은 본래의 Corr에 다른 변수의 영향이 섞여 있었음을 말해준다.
Generalization
위의 Exercise에선 2개의 독립변수 였기 때문에 벤 다이어그램으로 쉽게 Partial Correlation을 구할 수 있었다. 그러나 $N$개 독립변수가 있는 상황이라면 Partial Correlation을 어떻게 구해야 할까? 🤔
방법은 Linear Regression의 잔차(Residual)를 활용하는 것이다!
먼저 RV $X$, $Y$에 대해 $Z$를 Partialling Out한 Partial Correlation $\rho_{XY \cdot Z}$를 구해보자.
먼저 $Z$를 $X$, $Y$에 대해 Linear Regression Fitting을 한다.
\[w^{\ast}_X = \underset{w}{\text{argmin}} \left\{ \sum^N_{i=1} = (x_i - w \cdot z_i)^2 \right\}\] \[w^{\ast}_Y = \underset{w}{\text{argmin}} \left\{ \sum^N_{i=1} = (y_i - w \cdot z_i)^2 \right\}\]그리고 이를 통해 잔차(residual)을 구하면
\[e_{X, i} = x_i - w^{\ast}_X \cdot z_i\] \[e_{Y, i} = y_i - w^{\ast}_Y \cdot z_i\]이제 두 변수의 잔차에 대한 Correlation을 구하면, 그것이 두 변수의 Partial Correlation이다!
\[\rho_{XY\cdot Z} = \text{Cor}(e_{X}, e_{Y})\]왜 이렇게 구하는가?
위에서 Partialling Out할 독립변수를 가지고 Linear Regression을 한 후, 잔차(residual)를 기준으로 Partial Correlation을 구했다. 왜 이렇게 한 걸까?
일단 여기서 “잔차”의 의미는 말 그대로 독립변수 $Z$의 영향력을 제외한 이후의 데이터를 말한다. 여기까지는 자연스러운데, 왜 독립변수 $X$에도, 종속변수 $Y$에 대해서도 잔차를 구했을까?
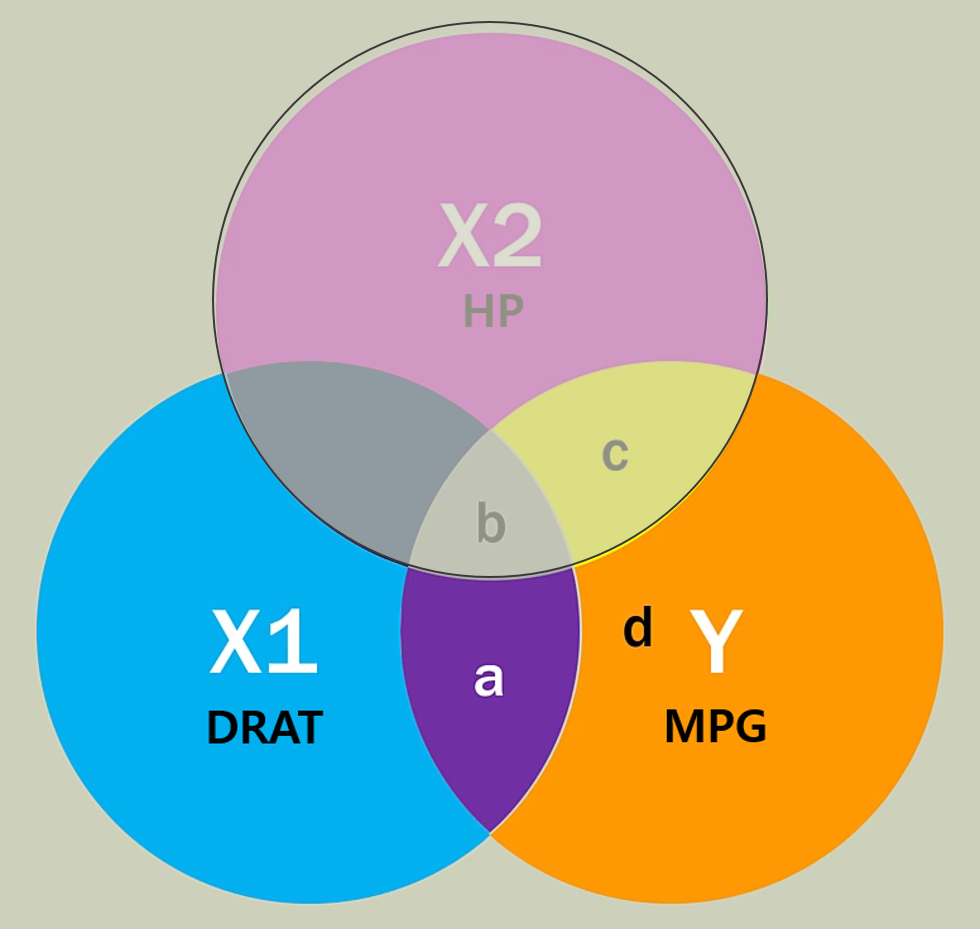
$X2$를 $X1$에도 $Y$에도 빼주었다.
다시 벤 다이어그램으로 돌아와보자. 우리는 $X1$, $Y$의 Partial Corr를 구하기 위해 $X1$와 $Y$에서 $X2$와 겹치는 부분을 싸-악 날려주었다. 독립변수, 종속변수 양쪽 모두 Partialling Out할 변수의 영향력을 제거해줘야 하는 것이다!
다시 Generalization
마지막으로 동일한 상황에서 Partialling Out하는 독립변수가 $n$개 인 $\mathbf{z} = \left\{ z_i \right\}_n$ 상황만 살펴보자.
\[\mathbf{w}^{\ast}_X = \underset{\mathbf{w}}{\text{argmin}} \left\{ \sum^N_{i=1} = (x_i - \left< \mathbf{w}, \mathbf{z} \right>)^2 \right\}\] \[\mathbf{w}^{\ast}_Y = \underset{\mathbf{w}}{\text{argmin}} \left\{ \sum^N_{i=1} = (y_i - \left< \mathbf{w}, \mathbf{z} \right>)^2 \right\}\]이를 통해 잔차(residual)을 구하면
\[e_{X, i} = x_i - \left< \mathbf{w}^{\ast}_X, \mathbf{z}_i \right>\] \[e_{Y, i} = y_i - \left< \mathbf{w}^{\ast}_Y, \mathbf{z}_i \right>\]이제 두 잔차에 대한 Correlation을 구하면,
\[\rho_{XY\cdot \mathbf{z}} = \text{Cor}(e_{X}, e_{Y})\]맺음말
Partialling Out, Regression Fitting을 통해 다른 RV의 영향력을 없애는 방법이었다. 새롭게 배운 요 테크닉, 다른 곳에 써볼 수 있지 않을까?
이 Partial Correlation은 시계열 데이터를 EDA하는 기법 중 하나인 Auto-Correlation과 Partial Auto-Correlation을 공부하면서 요 개념이 필요해 한번 정리하게 되었다. 이어지는 “ACF & PACF” 포스트에서 요 개념을 잘 활용해보자 😉
