ARMA & ARIMA Model

ARMA Model

AR 모델과 MA 모델은 각각 아래와 같은 상황에서 사용했었다.

• You would choose an AR model if you believe that “previous observations have a direct effect on the time series”.
• You would choose an MA model if you believe that “the weighted sum of lagged errors have a direct effect on the time series”.

그러나 AR과 MA 그 어느 것도 세상의 모든 시계열을 모델링할 수 있는 건 아니다.

ARMA 모델은 AR 모델과 MA 모델을 결합한 모델이다. 수식은 아래와 같다.

Definition. ARMA Model

\[X(t) = \left( \phi_0 + \phi_1 X(t-1) + \cdots + \phi_p X(t-p) \right) + \left( \epsilon(t) + \theta_1 \epsilon(t-1) + \cdots + \theta_q \epsilon(t-q) \right)\]

where all $\epsilon(t)$ are white noise.

보통 $\phi_0$는 시계열의 평균 $\mu = E \left[ X(t) \right]$로 둔다.

Hyper-parameter는 몇개의 Lag와 몇개의 Lagged Error를 쓸 것인지에 대한 $p$와 $q$ 값이다.

\[\text{ARMA}(p, q)\]

라고 표현한다.

MA로 모델링하기 위해선 시계열 데이터가 “정상성”을 가져야 했다. 따라서 ARMA 모델도 마찬가지로 “정상성”이 있는 시계열을 모델링하는데 사용한다.

ARIMA Model

그럼 비정상성 시계열에선 어떻게 해야할까? 답은 간단하다. 👏 <차분(Differencing)>을 해서 데이터를 정상성 시계열로 변환해주면 된다! ARIMA 모델을 ARMA 모델에 $d$회 차분을 수행한 모델이다!

이때, ARIMA 모델에서 “I”는 차분(Differencing)의 “D”가 아니라 “Integrated”의 “I”이다.

Definition. ARIMA Model

\[X'(t) = \left( \phi_0 + \phi_1 X'(t-1) + \cdots + \phi_p X'(t-p) \right) + \left( \epsilon(t) + \theta_1 \epsilon(t-1) + \cdots + \theta_q \epsilon(t-q) \right)\]

where all $\epsilon(t)$ are white noise.

$X’(t)$ means 1st differenced time series, $X^{(d)}(t)$ means $d$-order differenced time series.

결국, ARIMA는 $d$번 차분으로 정상성을 확보한 시계열에 ARMA로 모델링한 것에 불과하다!

Hyper-parameter에 몇번 차분을 수행했는지에 대한 $d$가 추가되었다.

\[\text{ARIMA}(p, d, q)\]

Example

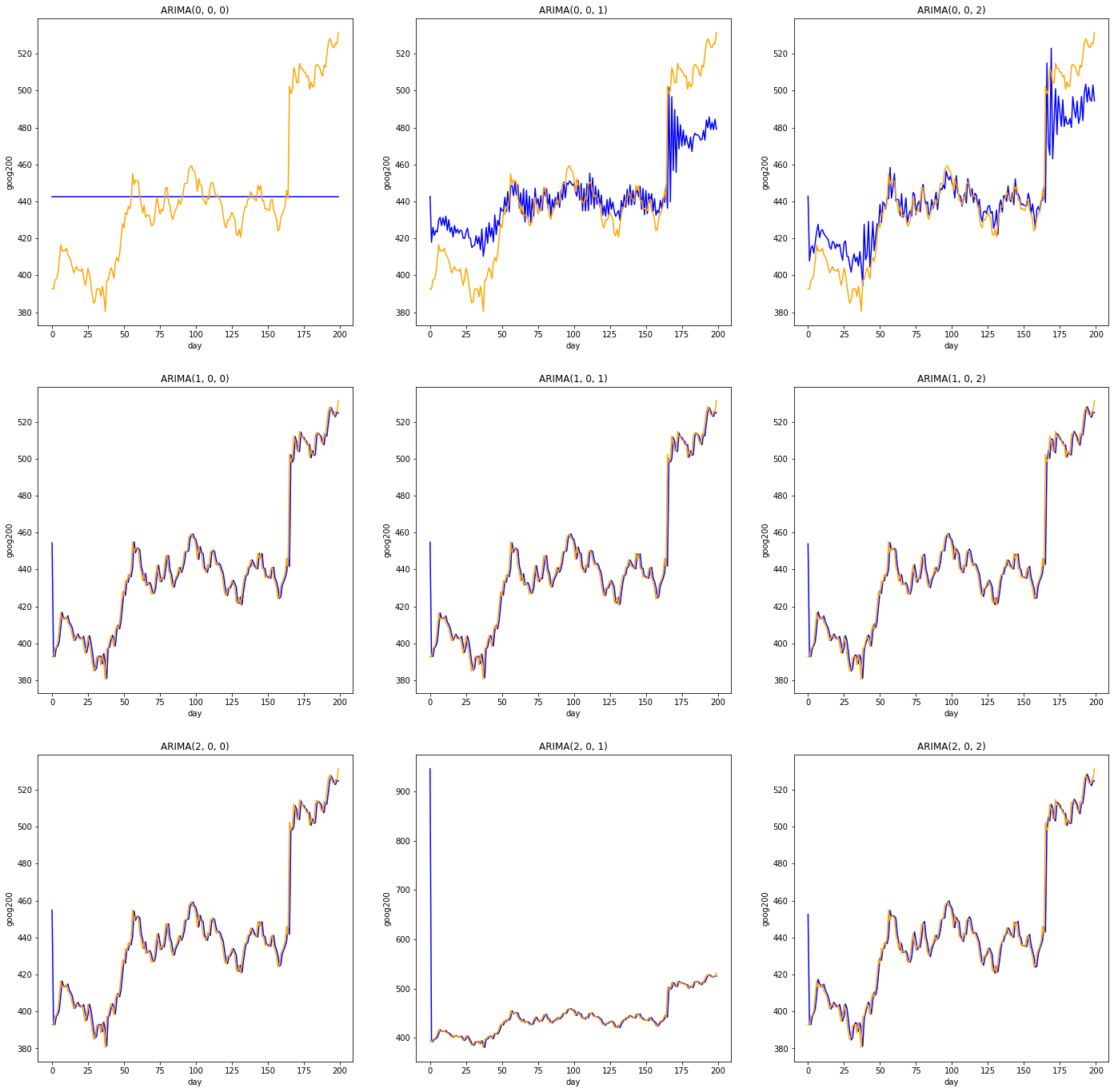
goog200 데이터에 대해 $d = 0$으로 두고, $p$와 $q$를 0부터 2까지 변화시킨 결과이다. 생각보다 Fitting이 잘 되는 것을 볼 수 있다.

여기서는 ARIMA 모델 예측의 대략적인 그림만 보고, Hyper-parameter를 결정하는 구체적인 방법은 별도의 포스트에서 다루도록 하겠다. 👏

Reference

• Wikipedia: Autoregressive integrated moving average