Poincaré Map

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

요 내용은 학부 2학년의 미분방정식(Math2xx) 수업이 아니라 학부 4학년의 상미분방정식론(Math4xx)에서 다룬 내용입니다.

Express ODE with initial value

시간 $t$에 의존하는 어떤 함수 $x(t)$를 생각해보자. 그리고 이 함수 $x(t)$는 ODE를 만족한다. 예를 들어 아래와 같은 형태일 수 있다.

• $x’ = a x$: exponential growth/shrinking
• $x’ = x(1-x)$: logistic population model

대부분의 ODE의 해 $x(t)$가 그렇듯 초기값 $x_0$에 따라서 함수의 양상이 달라질 수 있다.

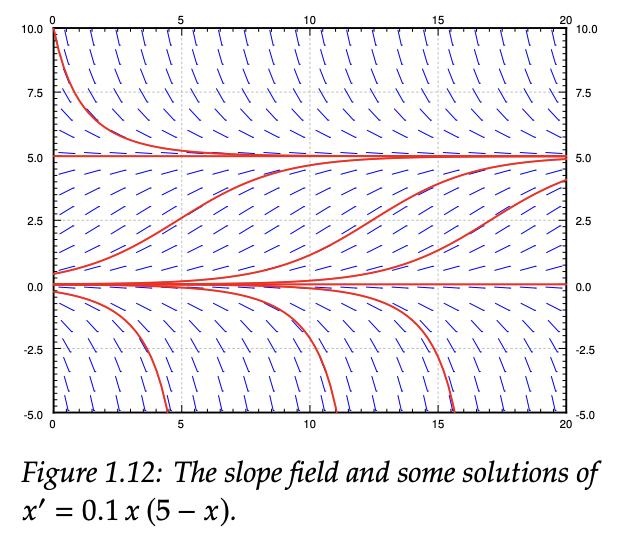Notes on Diffy Qs: Differential Equations for Engineers, Jiří Lebl

예를 들어, logistic population model에서는 초기 인구 값이 $0 < x_0 < x_1$라면, 인구 한계 $x_1$를 향해 증가하고, $x > x_1$ 였다면 인구 한계를 향해 인구가 감소한다.

지금까지 미분방정식에서는 solution function을 표현할 때, $x(t) = c_1 e^{\lambda t} + \cdots$와 같이 표현하고, $c_1$과 같은 계수값은 초기값 $x_0$을 대입해 구하는 방식으로 동작했다.

그러나, 이제는 시간 $t$와 초기값 $x_0$을 모두 고려한 solution function를 아래와 같이 정의해 사용하고자 한다. 이것은 우리가 위에서 살펴본 Logistic Model의 Solution Graph를 함수로 옮긴 것이라고 보면 된다.

\[\phi(t, x_0): \mathbb{R} \times \mathbb{R} \rightarrow \mathbb{R}\]

• It represents an point on solution graph.
• It means the value of the system when it starts from $x_0$ and time $t$ flows.
• Sometimes we write this function as $\phi_t (x_0)$.

Poincare Map

위의 Population Model은 그렇지 않았지만, 어떤 경우에는 ODE 함수가 어떤 주기성을 가지고 있을 수도 있다.

• $x’ = ax - h (1 - \sin (\omega t))$
• $x’ = x(1-x) - h (1 - \sin (\omega t))$

이때, 초기값 $x_0$에서 주기 $\omega$ 만큼 시간이 지난 후의 함수값 $\phi(\omega, x_0)$를 “Poincare Map”라고 정의한다.

[Poincare Map]

\[P(x_0) = \phi(\omega, x_0)\]

the value of the solution when one period $\omega$ has left.

만약, 초기값 $x_0$가 fixed point(or equilibrium point)라면, 아래와 같은 식이 성립하게 된다.

\[P(x_0) = \phi(\omega, x_0) = x_0 = \phi(0, x_0)\]

The key idea is to look at the fate of an arbitrary initial value $x_0$ after one period.

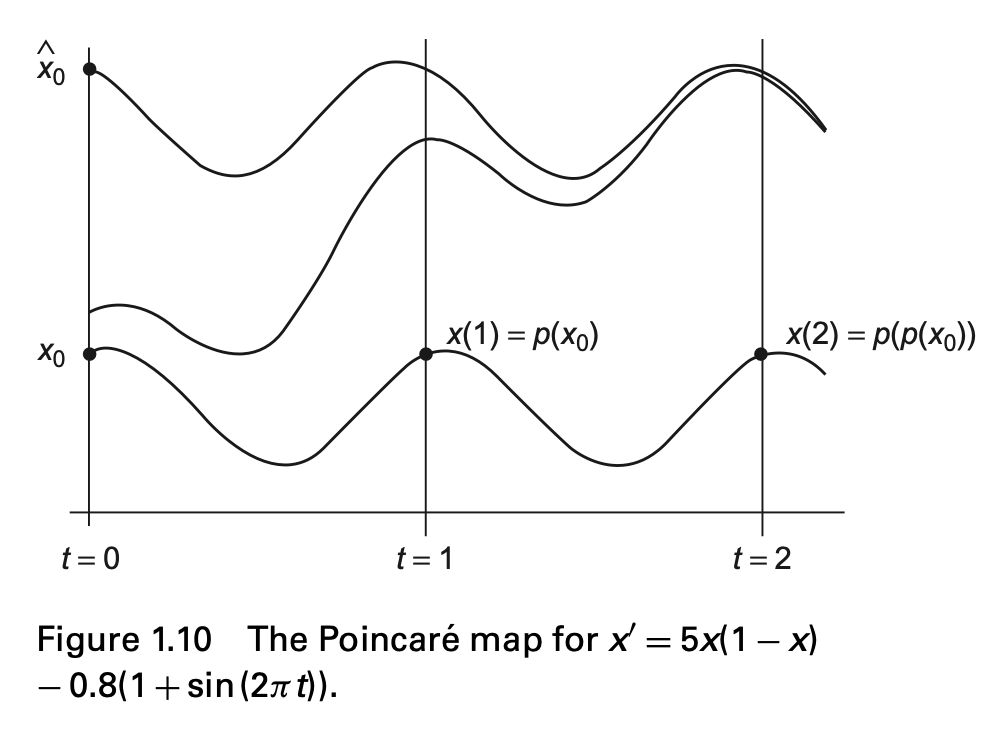Morris, Differential Equations, Dynamical Systems & An Introduction to Chaos 3rd Edition

위의 그림은 주기를 $\omega = 1$라고 했을 때의 Poincare Map을 그린 모습이다. 각각의 초기값에서 시작해 주기가 지날 때마다 함수값이 어떻게 변화하는지를 파악하기 쉽다.

Orbit

유의할 것은 Poincare Map도 여전히 함수이다. 그래서 이것을 어떤 초기값 $x_0$에 대해 여러번 적용할 수 있다.

\[x_0 \rightarrow P(x_0) \rightarrow P(P(x_0)) \rightarrow P(P(P(x_0))) \rightarrow \cdots\]

우리는 이렇게 어떤 점 $x_0$에서 시작해 Poincare Map을 적용한 모든 결과를 모아서 집합을 정의할 수 있는데, 이를 “Orbit”라고 부른다.

이때, 집합 Orbit은 유한 크기일 수도 있고, 무한 크기를 가질 수도 있다. 만약 Poincare Map이 어떤 초기값에 대해 $P^n(x_0) = x_0$하는 성질을 가지고 있다면, 그 Orbit은 유한 집합일 것이고 그 크기는 $n$일 것이다. 반대로 $P^n(x_0) = x_0$를 만족하는 자연수 $n$이 없다면, Orbit의 원소는 무한히 많을 것이다.

지금은 그냥 집합에 대한 정의만 하고 넘어가지만, 뒤에 “Dynamical Systems”에 대해 살펴볼 때 한번더 만나게 될 것이다 ㅎㅎ 지금은 그냥 분량 채우기 위해 적은 것 ㅋㅋ

On the view of trajectory

요건 Poincare Map을 이해해보려고, 인터넷을 떠돌다가 발견한 영상인데, 엄밀한 정의 없이 그림을 통해 Poincare Map이 뭔지 설명하고 있다. 단순하게 생각하면, 어떤 Curve와 Trajectory가 만나는 지점 $x_k$가 있고, 그 점에서 출발 했을 때 다음에 만나는 지점을 $P(x_k) = x_{k+1}$로 정의한다는 컨셉이다.

영상에서는 주기 $\omega$에 대한 언급이 전혀 없는데, 아마 Curve $\Sigma$과 궤적이 만나는 순간을 한 주기를 돌은 것으로 한 것 같다. 4학년 미방 수업 때는 이런 관점을 채택하지는 않지만, 궤적을 분석함에 있어서는 흥미로운 관점인 것 같다.