Zero Eigen Value on Systems of ODEs

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

Example 1

Draw the phase portrait of $x’ = A x$ where

\[A = \left( \begin{matrix} 2 & 1 \\ 4 & 2 \end{matrix} \right)\]

.

먼저, eigen value를 구해보자.

\[(2 - \lambda)(2-\lambda) - 4 = 0\]

이므로, $\lambda_1 = 4$, $\lambda_2 = 0$이 된다.

$\lambda_1 = 4$의 eigen value는 하던대로 구하면 된다: $v_1 = (1, 2)$.

$\lambda_2 = 0$를 처음 봐서 좀 당황했는데, eigen value가 0일지다로 eigen vector는 구할 수 있다. $A v = 0 \cdot v = 0$의 식을 풀면 되기 때문이다. 이 경우는 $(1, -2)$로 나온다.

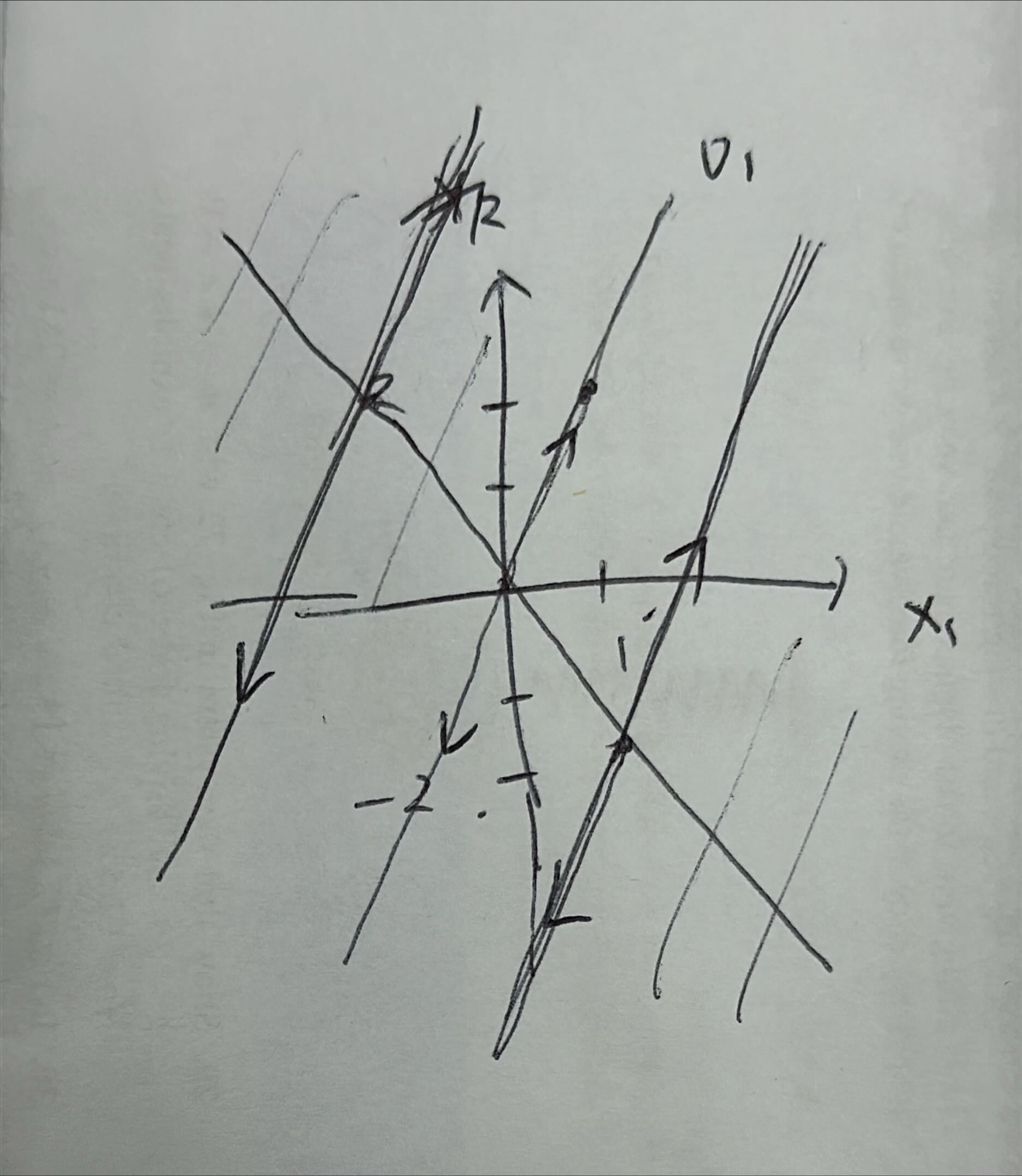
그리고 general solution을 구하면 아래와 같다.

\[x(t) = c_1 \left( \begin{matrix} 1 \\ 2 \end{matrix} \right) e^{4t} + c_2 \left( \begin{matrix} 1 \\ -2 \end{matrix} \right) e^{0t} = c_1 \left( \begin{matrix} 1 \\ 2 \end{matrix} \right) e^{4t} + c_2 \left( \begin{matrix} 1 \\ -2 \end{matrix} \right)\]

요 solution에 대한 Phase Portrait을 그려보면 아래와 같다.

$\lambda_1 = 4$이 양수이므로 벡터 $v_1$ 위에서 원점에 대해 나가는 방향으로 궤적이 움직인다. 반면에 벡터 $v_2$에서는 $t$에 대한 부분이 없고, 단순히 $v_1$ 궤적을 평행이동 시키는 역할을 한다.

이때, $v_2$가 평행이동할 때, 원점 $O$는 $v_2$ 직선 위를 움직이다. 따라서, Phase Portrait이 위의 그림과 같이 슬라이이딩? 하는 것처럼 보인다. 이때, $v_2$를 평형(equilibrium)이라고 하고, 이렇게 평형에서 멀어지는 방향으로 움직이는 것을 unstable이라고 한다.

Example 2 - Consider bifurcation

Draw the phase portrait of $x’ = A x$ where

\[A = \left( \begin{matrix} a & 1 \\ 2a & 2 \end{matrix} \right)\]

.

And find a bifurcation about $a$.

이번에도 eigen value를 구해보면, 하나가 0으로 나온다.

\[(a - \lambda)(2 - \lambda) - 2a = 0\]

• $\lambda_1 = a + 2$
• $\lambda_2 = 0$

그리고 대응하는 eigen vector를 구해보면,

• $\lambda_1 = a + 2$
  • $v_1 = (1, 2)$
• $\lambda_2 = 0$
  • $v_2 = (1, -2)$

eigen vector는 위의 예제를 풀었을 때와 동일하게 나온다!!

매개변수 $a$의 값에 따라 여러 Phase Portrait가 그려진다: bifurcation인 셈!

[case 1: $a = -2$]

$\lambda_1$도 $0$이 되어 버린다!!! 그런데, 다행인 점은 $v_1 \ne v_2$이다. 만약 $v_1 = v_2$ 였다면, generalized eigen vector를 구해줘야 한다. (generalized eigen vector를 구해야 하는 문제는 다음 포스트에서…)

general solution은 아래와 같다.

\[x(t) = c_1 \left( \begin{matrix} 1 \\ 2 \end{matrix} \right) + c_2 \left( \begin{matrix} 1 \\ -2 \end{matrix} \right)\]

이번에는 벡터 $v_1$, $v_2$에 둘다 $t$에 대한 부분이 없다. 따라서, 점이 그냥 $x_1 - x_2$ plane 위에서 고정점으로 존재한다.

[case 2: $a > - 2$]

$\lambda_1 > 0$이 되므로, 위에서 본 예제와 동일한 경우다. 스킵!

[case 3: $a < -2$]

$\lambda_2 < 0$이 되므로, 위에서 본 예제와 Phase Portrait이 동일하지만, 평형인 직선 $v_2$ 쪽으로 수렴하므로 stable 케이스다.

Reference

• Phase portrait with one zero eigenvalue