Jordan Block Case on Systems of ODEs

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

Jordan Block

\[J = \left( \begin{matrix} \lambda & 1 \\ 0 & \lambda \end{matrix} \right)\]

위와 같이 eigen value $\lambda$가 대각 영역에 존재하는 Upper Triangular 행렬을 말한다. 그냥 앞글자 J를 따서 $J$ 행렬로 표기하기도 한다.

eigen value를 구해보면 중근인 $\lambda$를 갖고, eigen vector 역시 중복(repeated)다: $v_1 = (1, 0)$.

이런 경우, generalized eigen vector를 구해야 한다.

Generalized Eigen Vector

본래 그냥 eigen value는 $(J - \lambda I) v_1 = 0$이 되는 $v_1$을 구하는 것이다. 그런데, Generalized Eigen Vector는 eigen vector $v_1$이 구하진 상태에서 구하는 벡터로 아래의 행렬식을 만족하는 $v_2$를 찾는다.

\[(J - \lambda I) v_2 = v_1\]

위의 식을 구해보면, $v_2 = (0, 1)$이 나오고, 정말 좋게도!! $v_1$과 직교한다 ㅎㅎ

Jordan Block Case of 1st Order Linear ODE

Solve the 1st order linear system

\[x' = J x\]

where $J$ is Jordan block described above.

앞에서 eigen vector $v_1$과 generalized eigen vector $v_2$을 구했으므로 이를 바탕으로 기저 해를 구해보면

\[x_1(t) = v_1 e^{\lambda t} = \left( \begin{matrix} 1 \\ 0 \end{matrix} \right) e^{\lambda t}\] \[x_2(t) = e^{\lambda t} (t v_1 + v_2) = \left( \begin{matrix} t \\ 1 \end{matrix} \right) e^{\lambda t}\]

그리고 general solution을 이 둘의 일차결합으로 표현하면 된다.

이것의 Phase Portrait을 그려보는게 좀 어려웠는데,

먼저, $x_1(t)$의 궤적을 생각해보면, 그냥 $x$축에서 원점에 가까워지거나, 멀어지는 형태이다.

여러운 건 $x_2(t)$인데, $(t, 1)$만 생각하면, $y=1$인 직선 위에서 $+x$ 방향으로 이동하는 궤적이었을 것이다. 그러나 $e^{\lambda t}$텀이 있기 때문에, 이를 같이 고려하면 $(t e^t, e^t)$인데… 뭔가 잘 안 떠올라서 Demos에 그려봤다 ㅋㅋ

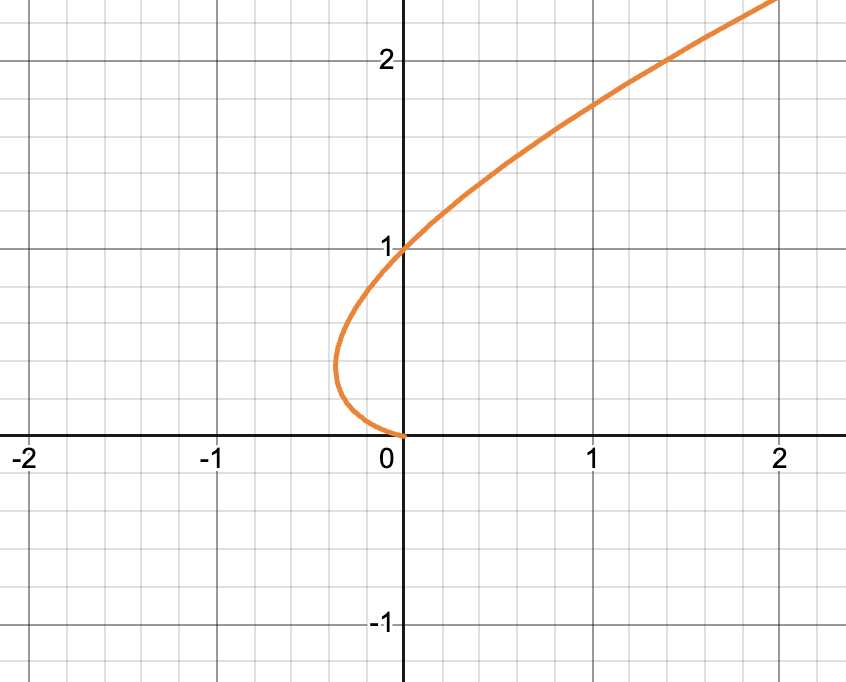
$t \rightarrow -\infty$라면, 원점 $O$에 가까워진다. 반면, $t = 0$부터는 x, y 값 둘다 무한을 향해 뻗어간다.

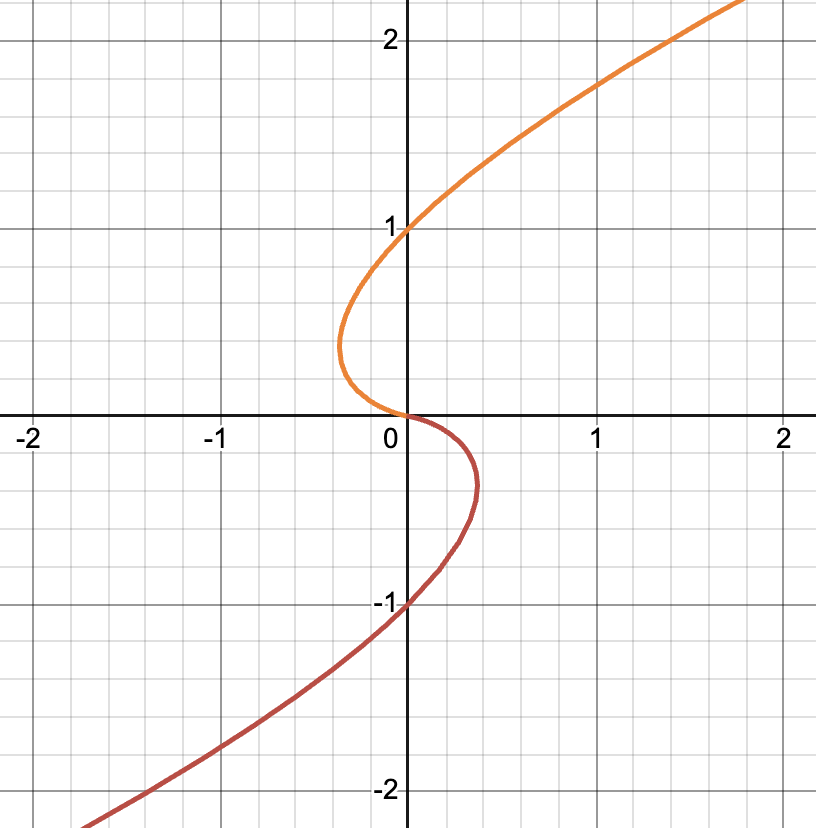
만약 $x_2(t)$에 계수 $c_2 = -1$를 곱해서 비교해보면 요런 소용돌이? 같은 패턴이 나온다.

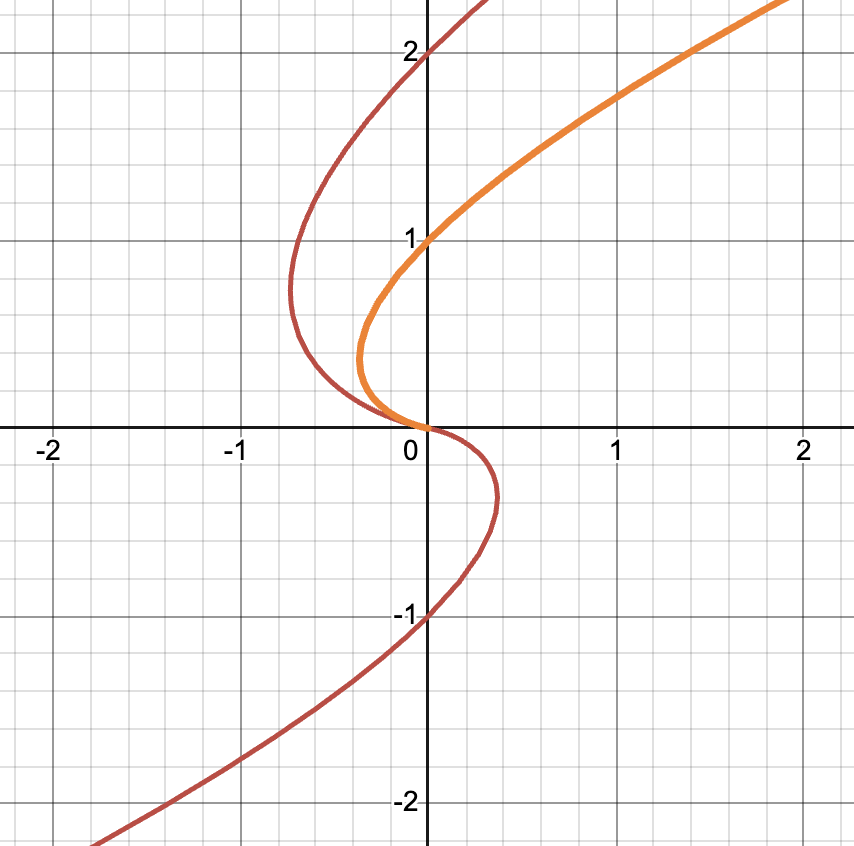
계수 $c_2 = 2$를 적용해서 또 중첩해서 보면 요런 느낌이다.

general solution을 종합해 Phase Portrait을 그려보면…

요런 $(1 + t, 1)$ 형태의 변환을 전단(sheer) 변환이라고 한다.