Lipschitz Constant

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

들어가며

경고하는데 여기서부터 진짜 완전히 새로운 내용입니다…;; 지금까지는 미분방정식의 심화 버전을 하는 느낌이었다면, 여기서부터 진짜 MATH4xx 과목의 위엄이 뭔지 작살나게 느낄 수 있습니다 ㅋㅋ

이 챕터의 목표는 ODE의 solution이 존재(Existence)하고 그리고 유일(Uniqueness)하다는 것을 보이는 것입니다. 그런데 저는 감자(🥔)니까 그 주변 곁다리부터 다가가보도록 하겠습니다.

[Existence and Uniqueness의 곁다리들]

순서는 상관없습니다.

• Lipschitz Constant 👋
• Picard Iteration
• Gronwall’s Inequality
• Some Preliminaries

Lipschitz Constant

세상에는 많은 2차원의 함수들이 존재할 것입니다. 그중에서 아래의 조건을 만족하는 함수도 있을 것입니다.

\[\| f(x) - f(y) \| \le M \| x - y \|\]

요렇게 보면 잘 와닿지 않는데 식을 조금 정리해주면

\[\frac{\| f(x) - f(y) \|}{\| x - y \|} \le M\]

요렇게 됩니다. 요건 함수의 기울기인데, 해석해보면 “함수의 기울기가 $M$을 넘어가지 않는다.“라고 해석할 수 있습니다. 그래서 위의 부등식을 더 간단하게 적으면 이렇게 적을 수 있습니다.

\[\| f'(x) \| \le M\]

우리는 함수 기울기의 상한선 $M$을 “Lipschitz Constant“라고 부르겠습니다. 수학적으로 정의하면 아래와 같습니다.

\[M := \sup_{x\ne y} \frac{\|f(y) - f(x)\|}{\| y-x\|} = \sup_x \| f'(x) \|\]

Examples

대표적으로 1차 함수 $y = 2x$는 $M = 2$로 Lipschitz Constant를 가집니다.

그리고 $y = \sin \pi x$도 $M = 2$로 Lipschitz 입니다.

Locally Lipschitz

본래 Lipschitz는 함수 정의역 범위에서 함수 기울기에 대해 논합니다. 즉, 전역적인 개념이죠. 그런데, 이걸 정의역 전체가 아니라 부분 영역에서 Lipz 조건을 만족하는 경우도 정의해볼 수 있습니다.

예시를 보면서 이해하는게 더 빠른데, $y = \sqrt{x}$ 함수를 떠올리면 됩니다.

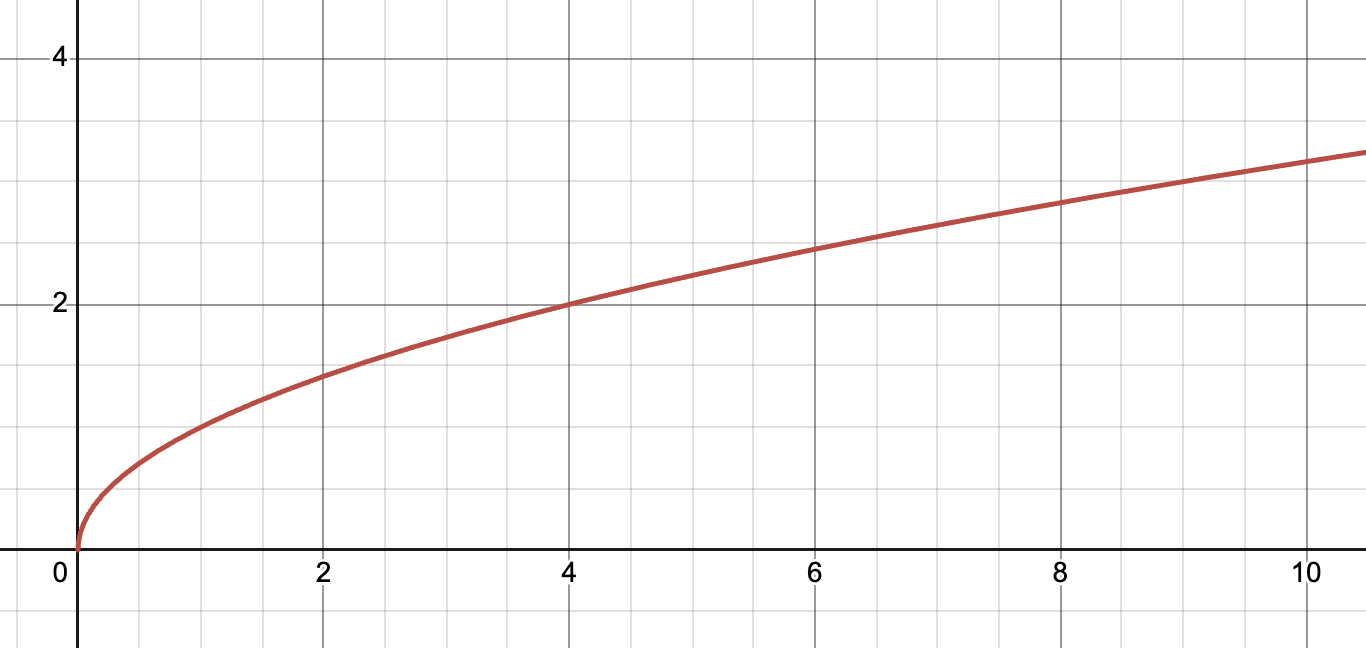Drawing by Demos

이 경우, $0$을 포함하는 부분 영역에서는 함수 기울기가 $+\infty$로 상한이 존재하지 않는 경우가 있어서 Lipschitz 하지 않습니다. 그러나, $0$을 포함하지 않는 부분 영역, 예를 들면 $[1, 2]$에서는 Lipschitz 조건을 만족하고 이런 함수들을 “Locally Lipschitz”라고 합니다.