The Stable Curve Theorem

복수전공하고 있는 수학과의 학부 졸업시험에 미분방정식이 있는 줄 알고, 시험 준비도 할 겸 복학할 때 “상미분방정식” 과목을 신청했습니다. 나중에 알고보니 미분방정식은 졸업시험 과목이 아니었습니다… OTL… 그래도 이왕 시작한 것 포기란 없습니다!! 💪 으랏차!! 상미분방정식 포스트 전체 보기

Non-linear Saddles

요런 Non-linear System에 대해 살펴보자.

\[\begin{aligned} x' &= x + y^2 \\ y' &= -y \end{aligned}\]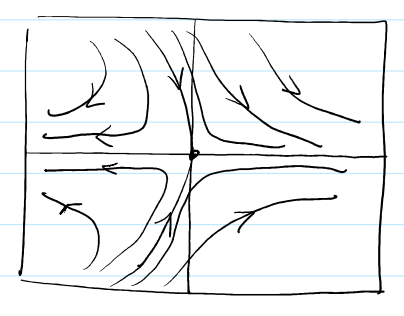

Class Material

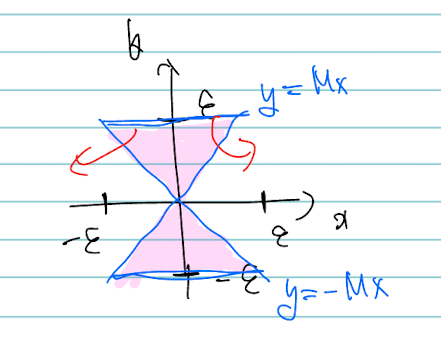
Phase Portrait만 보았을 때는 조금 휜 것만 빼면 $x’ = x, y’ = -y$인 Linear System과 크게 다르지 않다.

https://homepages.bluffton.edu/

조금 휜 것만 빼면 Linear System과 크게 다르지 않다

요게 이번 포스트에서 다룰 “The Stable Curve Theorem”의 핵심 문장이다! 😼

Linearized Saddles

위에서 봤던 Non-linear Saddles의 경우의 일반화된 형식은 아래와 같다.

\[\begin{aligned} x' &= \lambda x + f_1(x, y) \\ y' &= - \mu y + f_2(x, y) \end{aligned}\]

이때, $-\mu < 0 < \lambda$를 만족하고, 원점 $O$에 접근할 수록 $f_j(x, y)/r \rightarrow 0$로 수렴한다.

위의 System은 원점 $O$에서 Equilibrium point를 갖는데, 이를 “saddle“라고 한다. Linear System에서도 그렇게 불렀다! 다만, 여기선 추가된 non-linear 텀 $f_1(x, y)$, $f_2(x, y)$에 대해서도 원점으로 수렴한다는 조건이 필요했다.

https://homepages.bluffton.edu/

다시 한번 이 그림을 보자. y축이 stable line, x축이 unstable line이었다. 그런데, 요건 Linearized System이다. Non-linear System에서도 여전히 y축이 stable line, x축이 unstable line이라는 것은 절대 보장하지 않는다.

그러나, Non-linear System에서도 보존되는 성질이 있는데: Non-linear System에서도 Stable과 Unstable 성질을 갖는 두 곡선(curve)이 존재한다!

Stable Curve, and Unstable Curve

표기를 하나 정하고 논의를 이어가자. 그렇게 어렵지 않을 것이다 ㅎㅎ

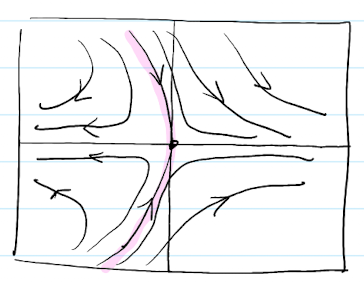
먼저 시간이 흐를수록 원점 $O$로 향해 가려는 초기값을 모은 곡선을 $W^s(0)$라고 정의하자. 이 곡선을 “stable curve”라고 한다.

반대로 시간이 흐를수록 원점 $O$에서 멀어지려는 초기값을 모은 곡선을 $W^u(0)$라고 정의하자. 이 곡선을 “unstable curve”라고 한다.

Class Material

맨 처음에 봤던 Non-linear System의 Phase Portrait이다. 여기에서 주목할 부분이 있는데, 바로 원점을 지나면서 y축에 Tangent한 곡선이다!! 이 곡선이 Linearized System에서 y축이었던 직선이다. Non-linear System이 되면서 이게 직선에서 곡선으로 변한 것!!

여기에서 본 “원점에 접하는 Sink 곡선”, 이걸 잘 기억하며 아래의 정리를 읽어보자.

The Stable Curve Theorem

Supp. the system

\[\begin{aligned} x' &= \lambda x + f_1(x, y) \\ y' &= - \mu y + f_2(x, y) \end{aligned}\]

satisfies $-\mu < 0 < \lambda$ and $f_j(x, y)/r \rightarrow 0$.

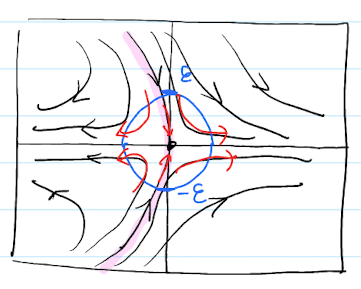
Then there exist an $\epsilon > 0$ and a curve $x = h^s(y)$ that is defined by $| y | < \epsilon$ s.t.

1. $h^s(0) = 0$
2. all solution starting on the curve remains on the curve for $t \ge 0$ and tend to the origin as $t \rightarrow \infty$.
3. the curve $x = h^s(y)$ passes through the origin tangent to the $y$-axis.
4. all other solutions starting in $B_\epsilon (0)$ leave the disk as time increases.

정리의 내용만 봐서는 좀 이해하기 어려웠다. 그래서 그림으로 이해해보면

Class Material

위의 그림에서 원점에 다가가는 한 곡선(curve)가 존재한다. 이 곡선이 stable curve $x = h^s(y)$이다. 그리고 이 곡선은 y축에 tangent 하다. $x = h^s(y)$라고 표현한 이유는 곡선이 $y$에 대한 $x$의 함수 꼴로 표현되기 때문!

그리고 이 stable curve $x = h^s(y)$가 아닌 주변의 모든 solution curve들은 시간이 지날수록 원점 인근 $B_\epsilon(0)$에서 멀어진다.

사실 위의 정리에서 나온 $x = h^s(y)$는 국소 범위 $B_{\epsilon}(0)$ 내에서 정의된 함수입니다. 그래서 이것을 “local stable curve”라고 합니다. 이것을 확장하여 시스템의 전체 상태 공간에서의 Stable Curve로 동작하는 것을 “complete stable curve” $W^s(0)$라고 합니다.

Proof: Brief Sketch

경계선이 $|x| = \epsilon$, $|y | = \epsilon$인 작은 사각 영역 위에서 초기 조건으로 시작하는 해들을 살펴보자. 이때, $\epsilon > 0$이 충분히 작은 영역이므로 System은 원점 근처에서 Linear System인 $x’ = \lambda x, y’ = - \mu y$과 비슷하게 행동합니다.

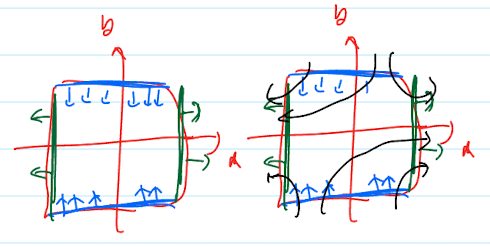
사각형의 Top/Bottom 경계인 $y = \pm \epsilon$에서는 벡터 필드가 사각형 내부를 향합니다. 반대로 Left/Right 경계인 $x = \pm \epsilon$에서는 벡터 필드가 사각형 외부를 향합니다.

사각형 Top 경계 $y = \epsilon$에서 초기 조건을 생각해봅시다. 일부 해는 왼쪽 경계를 통해 사각형을 떠날 것이고, 일부 해는 오른쪽 경계를 통해 사각형을 떠날 것입니다. 하나 확실한 것은 해가 왼쪽과 오른쪽 경계를 동시에 떠날 수는 없습니다. 이것은 Solution Curve가 연속적이기 때문입니다.

따라서, $y = \epsilon$ 위의 초기 조건 중 왼쪽으로 떠나는 해와 오른쪽으로 떠나는 해 사이에는 사각형을 떠지 않는 해가 반드시 존재합니다. 이 논리는 연속 함수가 두 점에서 상반된 부호(Left vs. Right)를 가지면, 그 사이에 0을 갖는 점이 반드시 존재한다는 “중간값 정리”의 논리와 유사합니다.

사각형을 떠나지 않는 초기 조건은 아래의 성질을 가질 것 입니다.

경계의 벡터 필드가 내부를 향하기 때문에, 이 해는 사각형 내부에서만 거동 한다 사각형 밖으로 나가지 않고, Stable Curve의 궤적을 따라 원점으로 수렴한다

그리고 이때의 Stable Curve가 $x = h^s(y)$가 됩니다.

Proof: Lemma 1

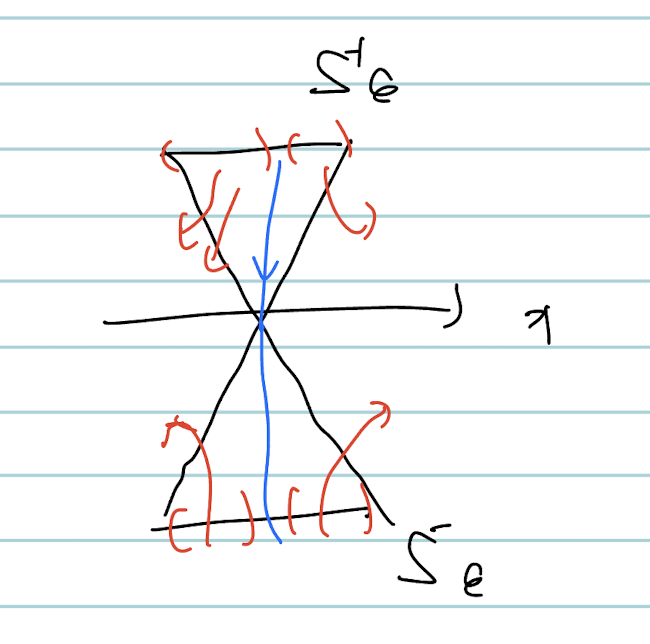
위의 셋업을 조금더 명확히 해보자. $B_\epsilon$은 $x = \pm \epsilon$, $y = \pm \epsilon$으로 둘러싸인 사각형 영역이다. 그리고 $B_{\epsilon}$의 $S_{\epsilon}^{\pm}$은 각각 Top/Bottom 경계를 말한다.

여기에 추가로 $C_M$라는 삼각뿔 모양의 영역을 추가로 정의한다. 이것은 $B_{\epsilon}$ 내부에 $|y|\ge M|x|$로 둘러싸인 영역이다.

처음에는 요런 셋업이 잘 와닿지 않았다. 그런데, 차분히 증명들을 따라가보니 그냥 Parameter가 $\epsilon$과 $M$ 2개인 상황이라고 받아들인 것 같다. (Dynamical System에서는 이런 상황이 꽤 많다.)

이제 요 상황에서 아래의 Lemma가 성립하는지 확인해보자.

[Lemma 1]

Given $M>0$, there exists $\epsilon > 0$ s.t. the vector field points outside $C_M$ for points on the boundary of $C_M \cap B_\epsilon$. Of course except at the origin.

[Setup]

Non-linear System에 있던 요 미분방정식을 살펴봅시다.

\[x' = \lambda x + f_1(x, y)\]

우리는 $B_\epsilon$ 내에서 선형 시스템으로 거동하길 바라기 때문에, 비선형 텀인 $f_1(x, y)$의 효과가 미미할 정도이길 바랍니다.

따라서, $\epsilon > 0$을 적절히 선택해 $f_1(x, y)$의 크기를 가능한 줄여야 합니다. 그래야 벡터 필드가 $\lambda x$에 의해 결정될 수 있기 때문입니다.

\[\| f_1(x, y) \| \le k r\]

로 설정한다면, $r \rightarrow 0$일 때, 비선형 텀의 영향이 0으로 수렴함을 보장할 수 있습니다. 이때, $k$ 값을 적절히 선택해야 하는데…

원뿔 $C_M$의 경계에서는 점이 $(x, Mx)$로 표현됩니다. 이것을 거리 $r$로 표현하면 아래와 같습니다.

\[r = \sqrt{M^2 + 1} \| x \|\]

위의 식을 잘 정리하면,

\[\begin{aligned} \| x \| &= \frac{r}{\sqrt{M^2 + 1}} \\ \lambda \| x \| &= \frac{\lambda}{\sqrt{M^2 + 1}} r \end{aligned}\]

이 됩니다. 우리는 $| f_1(x, y) | \ll \lambda x$를 만족하길 바라므로 위의 식을 조합하면…

\[\| f_1(x, y) \| \le \frac{\lambda}{\sqrt{M^2 + 1}} r\]

가 되도록 한다. 이때, 안정성을 좀더 여유롭게 보장하기 위해서, 상한을 절반으로 더 좁혀준니다.

\[\| f_1(x, y) \| \le \frac{\lambda}{2 \sqrt{M^2 + 1}} r\]

이 부등식이 $(x, y) \in B_{\epsilon}$ 내의 모든 점에 대해서 성립하도록 $\epsilon$을 잡습니다.

---

$ x > 0$인 Cone $C_M$의 오른쪽 경계에 대해 벡터 필드의 거동이 어떤지 살펴보자.

\[x' = \lambda x + f_1(x, Mx)\]

요 식은 아래를 만족한다.

\[\begin{aligned} x' &= \lambda x + f_1(x, Mx) \\ &\ge \lambda x - \| f_1(x, Mx) \| \end{aligned}\]

위의 부등식은 그냥 절댓값에 의해 생기는 부등식이라 자연스럽고, 이제 [setup] 단계에서 설정한 $ | f_1(x, Mx) |$에 대한 상한을 적용해보면…

\[\begin{aligned} x' &= \lambda x + f_1(x, Mx) \\ &\ge \lambda x - \| f_1(x, Mx) \| \\ &\ge \lambda x - \frac{\lambda}{2 \sqrt{M^2 + 1}} r \end{aligned}\]

그리고 Cone $C_M$의 경계에서 $r = \sqrt{M^2 + 1} | x |$이므로 이걸 대입하면…

\[\begin{aligned} x' &= \lambda x + f_1(x, Mx) \\ &\ge \lambda x - \| f_1(x, Mx) \| \\ &\ge \lambda x - \frac{\lambda}{2 \sqrt{M^2 + 1}} r \\ &= \lambda x - \frac{\lambda}{2 \cancel{\sqrt{M^2 + 1}}} (x \cancel{\sqrt{M^2 + 1}}) \\ &= \lambda x - \frac{\lambda x}{2} = \frac{\lambda}{2} x > 0 \end{aligned}\]

즉, Cone $C_M$의 오른쪽 경계에서는 벡터 필드가 오른쪽 방향인 $x’ > 0$의 값을 갖는다.

---

[setup for $y$]

마찬가지로 같은 세팅을 $y$에 대해서도 수행한다.

\[\| f_2(x, y) \| \le \frac{\mu}{2\sqrt{M^2 + 1}} r\]

그리고 $y > 0$에 대해 같은 과정을 수행하면, $y’ < 0$의 결과를 얻는다.

---

이걸 종합하면, 첫번째 사분면(quadrant)에서 Cone의 경계에서는 벡터 필드가 바깥 방향으로 흐른다는 것을 알 수 있다.

다른 사분면에 대해서도 동일한 과정을 반복하면, 벡터 필드가 $C_M$의 바깥 방향으로 흐른다는 것을 알 수 있다. $\blacksquare$

[Lemma 1: re-view]

Given $M>0$, there exists $\epsilon > 0$ s.t. the vector field points outside $C_M$ for points on the boundary of $C_M \cap B_\epsilon$. Of course except at the origin.

Lemma의 증명 과정에서 우리는 $S^{\pm}_{\epsilon} \cap C_M$ 위의 점들이 초기값일 때, 어떤 점들은 오른쪽 방향으로, 그리고 어떤 점들은 왼쪽 방향으로 나간다는 것을 관찰하였다. 이 초기값 점들을 모아서 집합을 구성하자. 그러면 이 집합은 Open Set이고¹, 우리는 이 Open set이 “Single Open Interval“임을 다음 Lemma에서 보일 것이다.

Proof: Lemma 2

[Lemma 2]

Suppose $M > 1$. Then there exist an $\epsilon > 0$ s.t. $y’ < 0$ in $C^{+}_M$ and $y’ > 0$ in $C^{-}_M$.

* $C^{+}_M$은 $C_M$에서 x축 위의 부분을, $C^{-}_M$은 x축 아래 부분을 말한다. 수식으로 표현 하면 요렇다: $C^{+}_M = C_M \cap \left\{ y > 0 \right\}$

$C^{+}_M$에서 우리는 $|Mx| \le y$이다. 따라서 $C_M$ 영역 내부에 존재하는 한 점 $r = (x, y)$에 대해서 아래 부등식이 성립한다.

\[r^2 = x^2 + y^2 \le \frac{y^2}{M^2} + y^2\]

식을 정리하 $r$에 대한 부등식으로 바꾸면

\[r \le \frac{y}{M} \sqrt{1 + M^2}\]

이전의 Lemma 1에서 우리는 아래 조건을 만족하도록 $\epsilon$을 잡았다.

\[\| f_2(x, y) \| \le \frac{\mu}{2\sqrt{M^2 + 1}} r\]

위의 부등식을 조합하면, $C^{+}_M$ 영역에 존재하는 점들에 대해 아래가 성립한다.

\[\begin{aligned} y' &= -\mu y + f_2(x, y) \\ &\le -\mu y + \| f_2(x, y) \| \\ &\le -\mu y + \frac{\mu}{2\sqrt{M^2 + 1}} r \\ &\le -\mu y + \frac{\mu}{2\cancel{\sqrt{M^2 + 1}}} \frac{y \cancel{\sqrt{M^2 + 1}}}{M} \\ &\le \mu (-1 + \frac{1}{2M}) y \\ &\le - \frac{\mu}{2} y \end{aligned}\]

맨 마지막 부등식 $\le - \mu/2 \cdot y$는 $M>1$이기 때문에 그렇다.

마찬가지 방법으로 $C^{-}_M$에 대해 수행하면, $y’ \ge 0$라는 결과를 얻을 것이다. $\blacksquare$

[Lemma 2: re-view]

Suppose $M > 1$. Then there exist an $\epsilon > 0$ s.t. $y’ < 0$ in $C^{+}_M$ and $y’ > 0$ in $C^{-}_M$.

* $C^{+}_M$은 $C_M$에서 x축 위의 부분을, $C^{-}_M$은 x축 아래 부분을 말한다. 수식으로 표현 하면 요렇다: $C^{+}_M = C_M \cap \left\{ y > 0 \right\}$

이 보조정리가 무슨 의미가 있다는 것일까?

1. Solution Curve가 원점을 향하는 것이 아니라면, 시간이 지날 수록 어떤 Solution Curve도 $C_M$ 내에 존재할 수 없습니다.

이것은 $C_M$이 Conic Section 이기 때문인데, $C^{+}_M$에서는 $y’<0$이고, $C^{-}_M$에서는 $y’>0$이기 때문에 언젠가는 $C_M$을 벗어날 수 밖에 없습니다.

2. “Continuously Dependence Theorem”에 의해 $S^{+}_{\epsilon}$에서 오른쪽으로 나가는 점들과 왼쪽으로 나가는 점들의 집합은 항상 single open interval일 수 밖에 없습니다.

2번 성질은 원점 $O$가 $\{ 0 \}$인 closed set이기 때문입니다.

Proof: Lemma 3

다음으로 주정할 것은 초기값들이 모여있는 $S^{+}_\epsilon$에서 원점 $O$를 향해 하는 점이 단 하나 존재한다는 것을 확인하고자 합니다.

[Lemma 3]

The solution staring from $S^{+}_\epsilon$ tends to $O$ is a single point.

Sorry

요 부분은 증명을 읽어봐도 도저히 모르겠습니다 ㅠㅠ 좌표 변환을 뭔가 하는데, 좌표 변환을 왜 그렇게 잡는지도 전혀 모르겠습니다… 교수님께 질문이라도 보내보겠습니다;;

High-dimensional Saddles

$X’ = F(X)$인 System에 $X_0$가 Fixed point로 $F(X_0) = \mathbb{0}$를 만족합니다. 이때, $k$개 eigenvalues는 negative real part를 가지고, $n-k$ eigenvalues는 positive real part를 가집니다. negative real part는 stable 성질을 가지고, positive real part는 unstable 성질을 가집니다.

예제를 통해 이 성질을 좀더 살펴봅시다.

Consider the system

\[\begin{aligned} x' &= -x \\ y' &= -y \\ z' &= z + x^2 + y^2 \end{aligned}\]

위의 시스템은 $z’ = z + x^2 + y^2$ 부분 때문에 Non-linear System 입니다. 그리고 Linearized System에서의 eigenvalue는 -1, -1, 1로 나오게 됩니다. Non-linear System 자체를 $zx$, $yz$ 변수만 조합해서 살펴보면 아래와 같습니다.

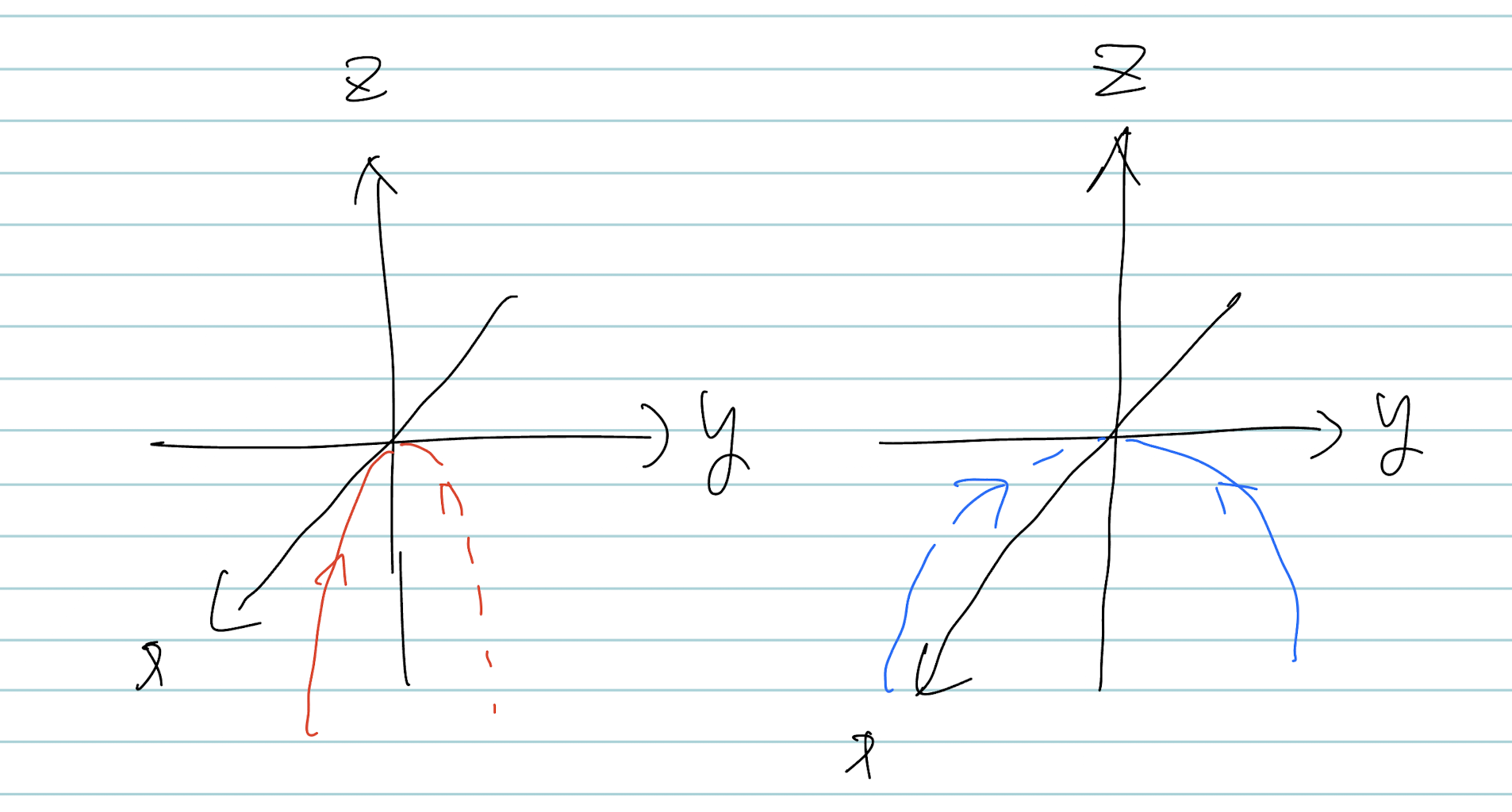
이제 이걸 아래와 같이 좌표 변환을 수행합니다. 그러면

\[\begin{aligned} u &= x \\ v &= y \\ w &= z + \frac{1}{3} (x^2 + y^2) \end{aligned}\]

이 좌표 변환을 적용하면, Non-linear System이 Linear System으로 바뀝니다.

\[\begin{aligned} u' &= -u \\ v' &= -v \\ w' &= w \end{aligned}\]

$w’ = w$에 대한 부분은 실제로 선형 시스템으로 잘 변환되는지 조금은 궁금했는데, 차분하게 $w’$에 대한 식을 정리하면 저렇게 나옵니다!

그러면, $w = 0$에서 Linear System이 Stable Plane을 그리게 됩니다.

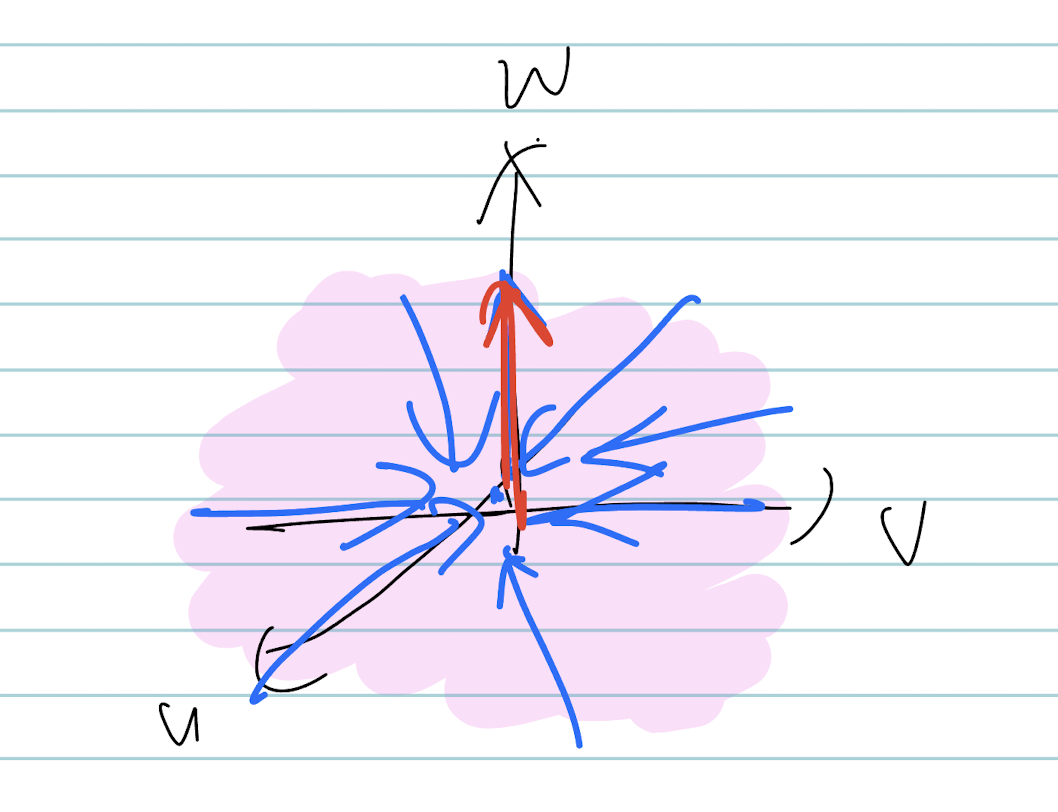
그리고 좌표변환한 것을 다시 역변환 하면, 그 $w = 0$ plane은 $xyz$ 공간에서 요런 surface가 됩니다.

\[z = -\frac{1}{3}(x^2 + y^2)\]

시각화 하면 아래와 같습니다.

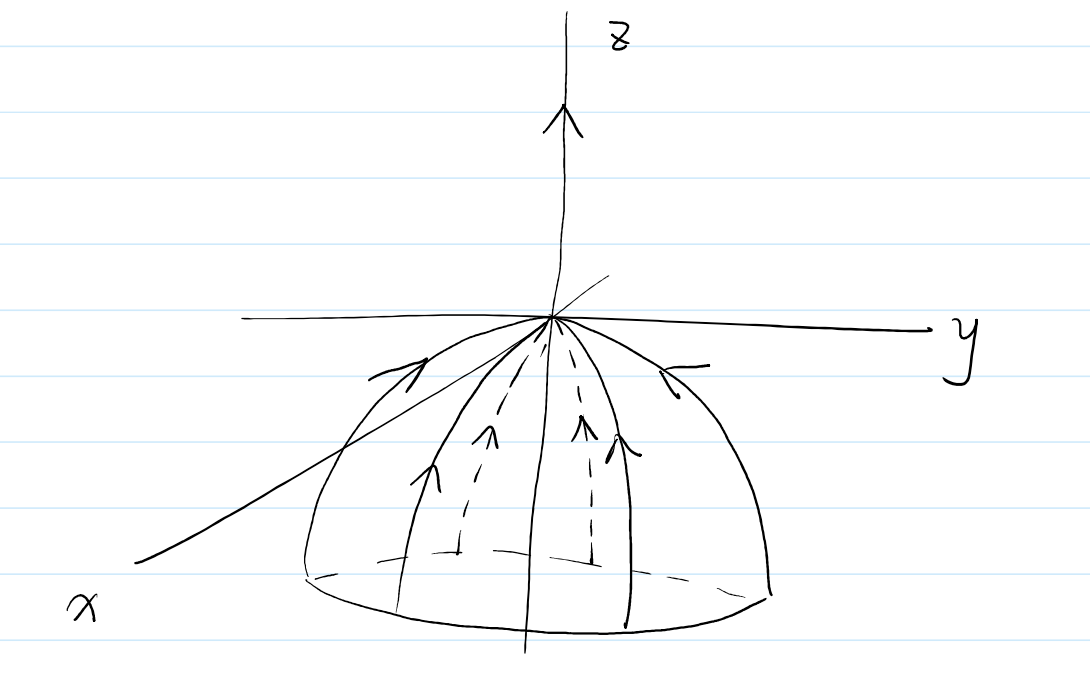Class Material

맺음말

상미분방정식 수업의 내용이 뭔가, 정리 자체는 되게 짧고, 시각적으로 직관적인데 증명은 내용이 엄청 길어지는 것 같다… 😵‍💫

암튼 곧 종강이니 화이팅!!

1. Continuously Dependence Theorem 때문이라고 함. 수업 교재 7.3의 내용이라고 함. (사실 저 챕터 너무 어려워서 이해 못 함 ㅠㅠ) ↩