Subgraph Matching Problem

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

Introduction

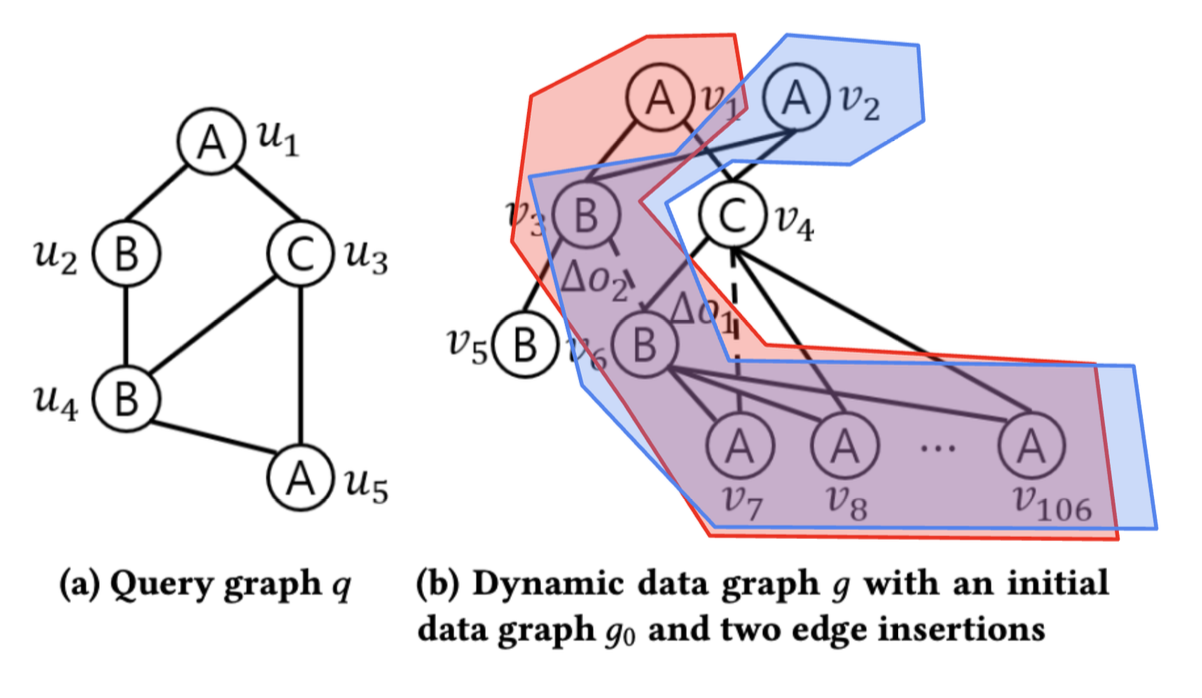
이번 포스트에서는 SymBi 논문에서 푸려고 하는 문제인 “CSM(Continuous Subgraph Matching)” 문제와 관련된 용어가 개념을 정리하고자 합니다. 먼저 조금 친숙해지기 위해 CSM 문제에 대해 기술하면,

쿼리와 데이터 둘다 그래프의 형태로 주어집니다. “Subgraph Matching” 문제는 주어진 데이터 그래프 위에서 쿼리 그래프가 부분 그래프로 얼마나 존재하는지 찾는 문제가 됩니다.

“Continuous” SM 문제는 데이터 그래프에 Graph Update Stream $\Delta o_i$가 제시됩니다. Update Stream은 엣지 추가가 될 수도 있고, 엣지 삭제가 될 수도 있습니다.

엣지 추가로 인해 Subgraph Matching이 추가된다면 positive match, 엣지 삭제로 인해 Subgraph Matching이 없어진다면 negative match라고 합니다.

그리고 포스트에서 다루는 용어와 개념은 “SymBi” 논문을 기준으로 작성 되었음을 미리 밝힙니다!

Terminologies

Graph

Undirected, Connected, and vertex-labeled graph를 가정 합니다. 그래프 $g$의 각 요소는 아래와 같습니다.

• $V(g)$
  • set of vertices
• $E(g)$
  • set of edges
• $l_g: V(g) \rightarrow \Sigma$
  • labeling function
  • $\Sigma$ is “set of labels”

그리고 그래프 $g$를 아래와 같이 표현한다.

\[g := (V(g), E(g), l_g)\]

Representation

별도 포스트?

Induced Subgraph

주어진 그래프 $g$에서 Subgraph를 만들 때, 그냥 만드는게 아니라 나이스만 Subgraph가 되도록 정의해야 합니다.

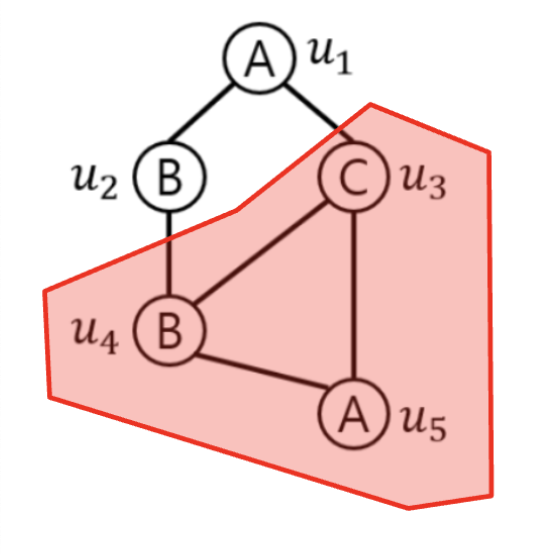
Given $S \subseteq V(g)$, a graph whose vertex set if $s$ and whose edge set consists of all the edges in $E(g)$ that have both endpoints in $S$.

쉽게 설명하면, Subgraph를 만들기 위해 뽑은 Vertex subset $S$에 대해서, 기존 그래프 $g$에서 subset $S$ 사이에 연결된 edge는 모두 유지하는 Subgraph를 말합니다.

Graph Matching Problem

Homomorphism

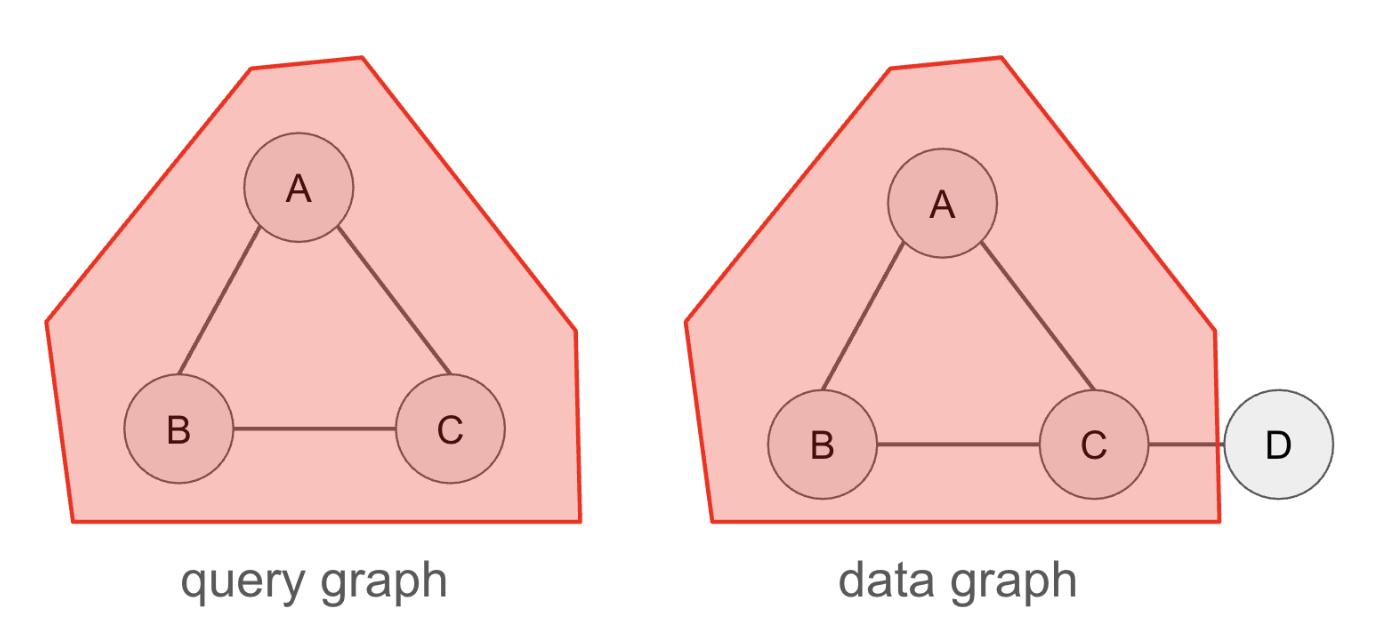
쿼리 그래프 $q$와 데이터 그래프 $g$가 있을 때, 두 그래프 사이의 매칭 상태에 대한 정의 입니다.

• Query Graph $q = (V(q), E(q), l_q)$
• Data Graph $g = (V(g), E(g), l_g)$

There exist a mapping $M: V(q) \rightarrow V(g)$ s.t.

1. For every $u \in V(q)$, $l_q(u) = l_g(M(u))$
2. For every $(u, u’) \in E(q)$, $(M(u), M(u’)) \in E(g)$

Embedding

an injective homomorphism s.t. $u \ne u’\implies M(u) \ne M(u’)$

Homomorphism 보다 더 강한 매칭 조건을 만족 합니다. 원본 그래프의 구조적 성질을 최대한 보존하는 그래프 매핑 방법 입니다.

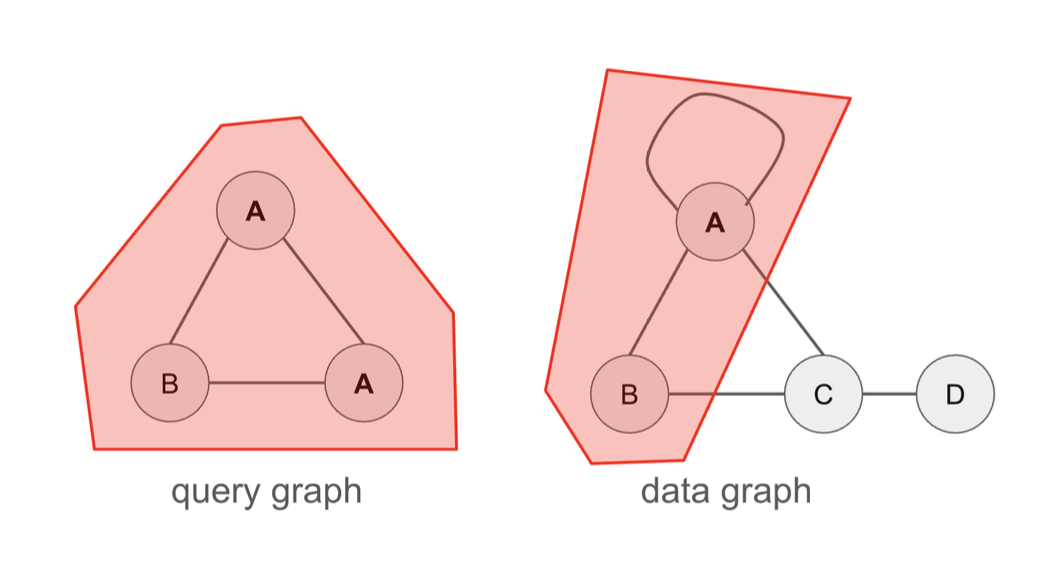
위 그림은 Homomorphism은 만족하지만, Embedding은 만족하지 않는 예시 입니다. 쿼리 그래프에서 $A$로 레이블된 두 노드가 데이터 그래프에서 같은 $A$ 노드로 매핑되었기 때문에 “injective” 조건을 만족하지 않습니다!

Partial Embedding

When induced subgraph of $q$ has embedding on data graph $g$.

쿼리 그래프의 “induced subgraph”에 대해서 임베딩이 존재하는 경우

Subgraph-isomorphism/homomorphism

Subgraph-isomorphism은 더 강한 조건으로 쿼리 그래프 $q$가 데이터 그래프 $g$의 부분 그래프로 정확히 일치합니다.

반면에 “Subgraph-homomorphism”은 좀더 느슨한 매핑으로 쿼리 그래프 $q$가 데이터 그래프 $g$에 구조적으로 대응 되지만, 일부 노드의 매핑이 겹치는 경우도 있습니다.

앞으로 전개되는 내용에서 그래프 쿼리 매칭을 찾는다는 것은 “subgraph isomorphism”을 만족하는 매칭을 찾겠다는 것을 말합니다!

How to find subgraph matching efficiently

DAG of query graph

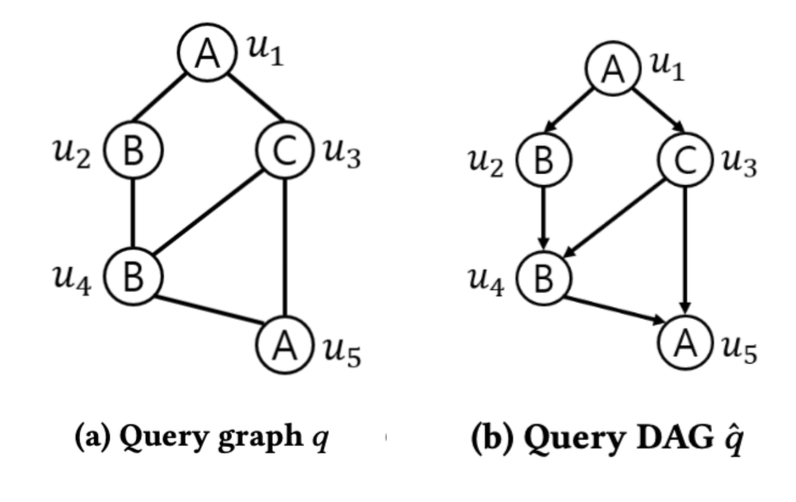
쿼리 그래프에서 임의로 루트 노드를 잡은 후, 이를 바탕 DFS 탐색을 하여 쿼리 DAG $\hat{q}$를 생성 합니다.

Path Tree of query graph

이때, 쿼리 DAG $\hat{q}$를 DFS 방법으로 순회하여 얻는 트리 그래프를 “Path Tree” $\hat{q}_T$라고 합니다.

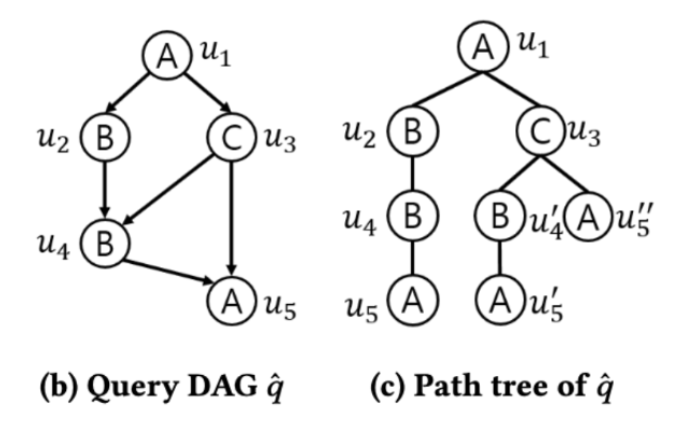
Path Tree는 DAG 쿼리를 다룰 때, 그래프의 전체 구조를 유지하면서도 검색을 빠르게 하도록 하는 쿼리 그래프의 변형 입니다.

Weak Embedding

For a rooted DAG $\hat{q}$ with root $u$,

a “weak embedding $M’$ of $\hat{q}$ at $v \in V(g)$” is defined as a homomorphism of the path tree of $\hat{q}$ in $g$ s.t. $M’(u) = v$

DAG 쿼리 $\hat{q}$에 대한 매핑을 바로 찾는게 아니라, 이것의 Path Tree 쿼리 $\hat{q}_T$를 만들고 이것에 대한 “Homomorphism” 매핑이 존재하는지 체크한 결과를 말합니다. 이때, Path Tree에 대한 Embedding을 찾는게 아니라 “homomorphism“이 존재하는지 찾는 것에 유의 합니다.

Weak Embedding은 매칭 여부를 빠르게 확인하기 위해 “완화된 매칭”입니다.

Example

아래는 논문에서 제시한 Weak Embedding의 예시 입니다. 여기에서 “weak embedding of $\hat{q}_{u_3}$ at $v_4$”를 찾을 수 있습니다. 대상이 되는 노드들을 쉽게 보기 위해 붉은 영역으로 표시하였습니다.

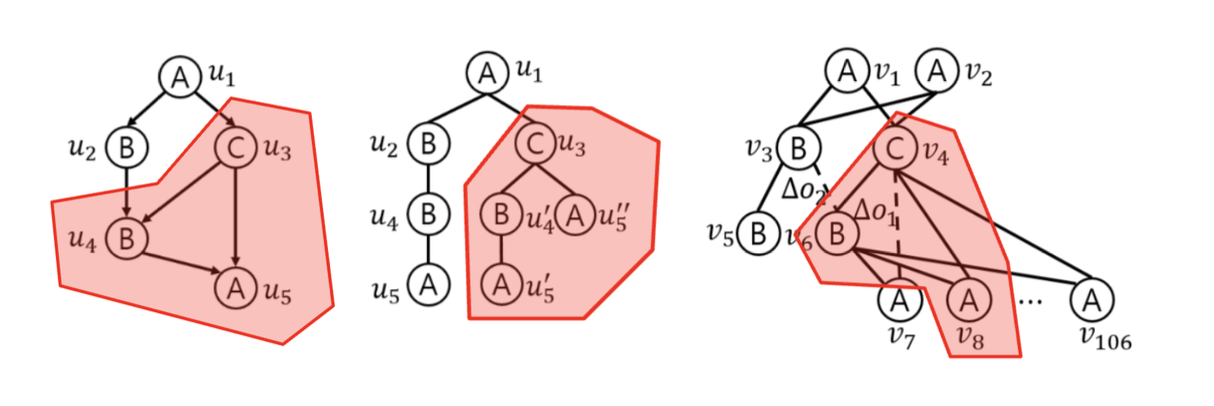
자세히 살펴보면, 예시는 나이스한 매핑이라서 sub-DAG $\hat{q}_{u_3}$에 대해 Embedding이 존재하는 경우 입니다만…! 설명을 위해 좀더 살펴보겠습니다.

먼저, 예시의 매핑은 Weak Embedding 입니다. 이유는 Path Tree에 대해 “homomorphism” 매핑이기 때문입니다. $M(u’_5) = M(u^{\prime\prime}_5) = v_8$이기 때문에 embedding이 아니라 homomorphism 입니다. 다만, DAG $\hat{q}$ 입장에서는 “Weak Embedding” 입니다.

Embedding and Weak Embedding

Every embedding of $q$ in $g$ is a weak embedding of $\hat{q}$ in $g$,

but the converse is not true

쿼리 그래프에 임베딩이 존재한다면, 쿼리 DAG에 대해서는 항상 “Weak Embedding”이 존재한다는 명제 입니다. 하지만, SymBi 논문에서는 이것의 대우 명제를 활용해 탐색 범위를 가지치기 하는데 사용합니다.

IF there exist no weak embedding of $\hat{q}$ in $g$,

then there no embedding of $q$ in $g$.

역명제는 거짓이라고 했는데, “Weak Embedding이 존재한다고 해서, Embedding이 존재하는 것은 아니다.” 이것도 쉽게 예시를 떠올려 볼 수 있습니다.

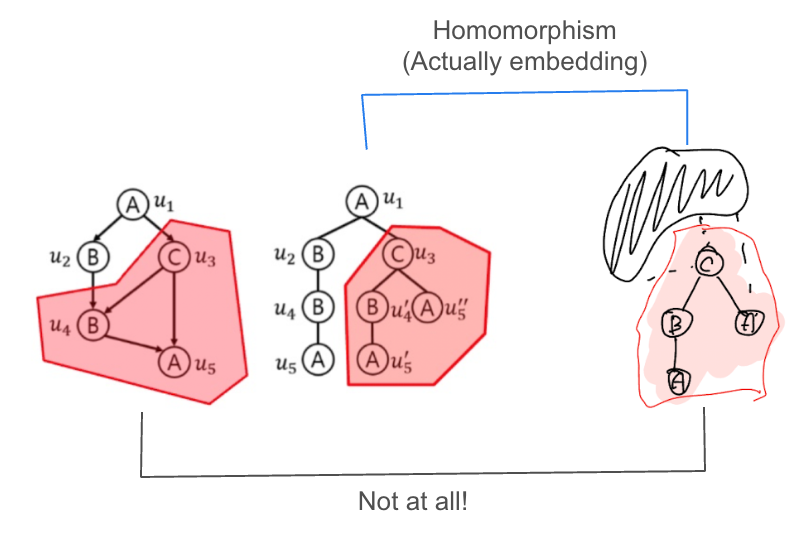
데이터 그래프에 Path Tree와 형상이 완전히 똑같은 매핑이 존재한다고 해봅시다. 즉, Path Tree에 대해 homomorphism이 아니라 embedding을 만족하는 경우 입니다. 그런데, 쿼리 DAG $\hat{q}$와 Path Tree $\hat{q}_T$가 서로 isomorphic 하지 않습니다. 이런 경우라면, Weak Embedding은 존재하지만, 이것이 Embedding이 되지는 못합니다!

단, Embedding이 되지 못하는 이유를 Path Tree에 대해 embedding이 존재하기 때문이라고 생각하면 안 되고, 쿼리 DAG와 Path Tree의 형상이 서로 다르면 이렇게 Weak Embedding에 대한 역이 성립하지 않는 경우가 발생할 수 있다고 받아들여야 합니다.

Backtracking

재귀적으로 모든 경우의 수를 탐색하는 기법 입니다. 이때, 유망하지 않은 경로는 조기에 포기(Pruning)하여 탐색 성능을 높일 수 있습니다. 그래서 완전 탐색(Brute-force)보다 효율적으로 원하는 조건을 탐색할 수 있습니다.

1. 가능한 해(Partial Solution)을 구성하고
2. 유효성을 검사함
   1. 이때, 조건을 만족하지 않으면, 포기하고 돌아감 = backtrack
   2. 조건을 만족하면, 계속 진행

백트래킹은 주로 아래의 문제들에 사용 합니다.

• 제약 충족 문제(Constraint Satisfaction Problems)
  • N-queen 문제
  • 스도쿠
  • 그래프 색칠 문제(Graph Coloring)
• 조합 및 순열 문제
  • 부분집합의 합 문제(Subset Sum)
  • 여행자 문제(TSP)
• 그래프 탐색
  • 미로 찾기(Maze Solver)

학부 알고리즘 수업과 인공지능 수업 때, 많이 배웠던 개념 입니다 ㅎㅎ

Ullmann’s backtracking

부분 그래프의 동형(subgraph isomorphism) 문제를 해결하기 위해 1976 Ullmann이 제시한 백트래킹 기반 알고리즘 입니다.

두 개의 그래프 $G$와 $H$가 있을 때, $H$가 $G$의 부분 그래프인지 판별하는 알고리즘 입니다.

1. 후보 행렬 생성
   1. $G$ 노드와 $H$ 노드 간의 매칭 후보를 찾아 기록합니다.
   2. 노드 레이블이 다르면 매핑이 전혀 안 되는 노드 쌍이니, 심플하게는 각 노드의 레이블이 같다면, 후보로 분류 합니다.
2. 재귀적으로 탐색
   1. 각 노드에 대해 가능한 매핑을 백트래킹 하며 탐색 합니다.
3. Pruning
   1. 유효하지 않은 매핑은 미리 제거하여 탐색 속도를 높입니다.
4. 매핑 검증
   1. 완성된 매핑이 그래프 구조를 유지하는지 확인 합니다.

Related Works

Symbi 논문에서 제시되었던 관련 논문들을 기준으로 나열 하였습니다.

• TurboIso (2013) [1]
• CFL-Matching (2016)
• DAF (2019)

이중에서 TurboIso 논문은 현재 졸업 연구 중인 연구실에서 게시한 논문 입니다! 추후에 읽고 내용을 정리하겠습니다.

맺음말

지금까지 “Subgraph Matching”에 대한 용어와 개념들을 살펴보았습니다. 이제는 본격적으로 졸업 연구에서 다루는 “Continuous Subgraph Matching” 문제에 대해서 살펴보겠습니다.

➡️ Continuous Subgraph Matching