Paper Reading: SymBi, Setup DCS

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

Dynamic Candidate Space (DCS)

“DCS”는 Symbi 논문에서 사용하는 자료구조로 Weak Embedding이 존재할 것 같은 후보를 빠르게 찾기 위해 사용하는 녀석 입니다.

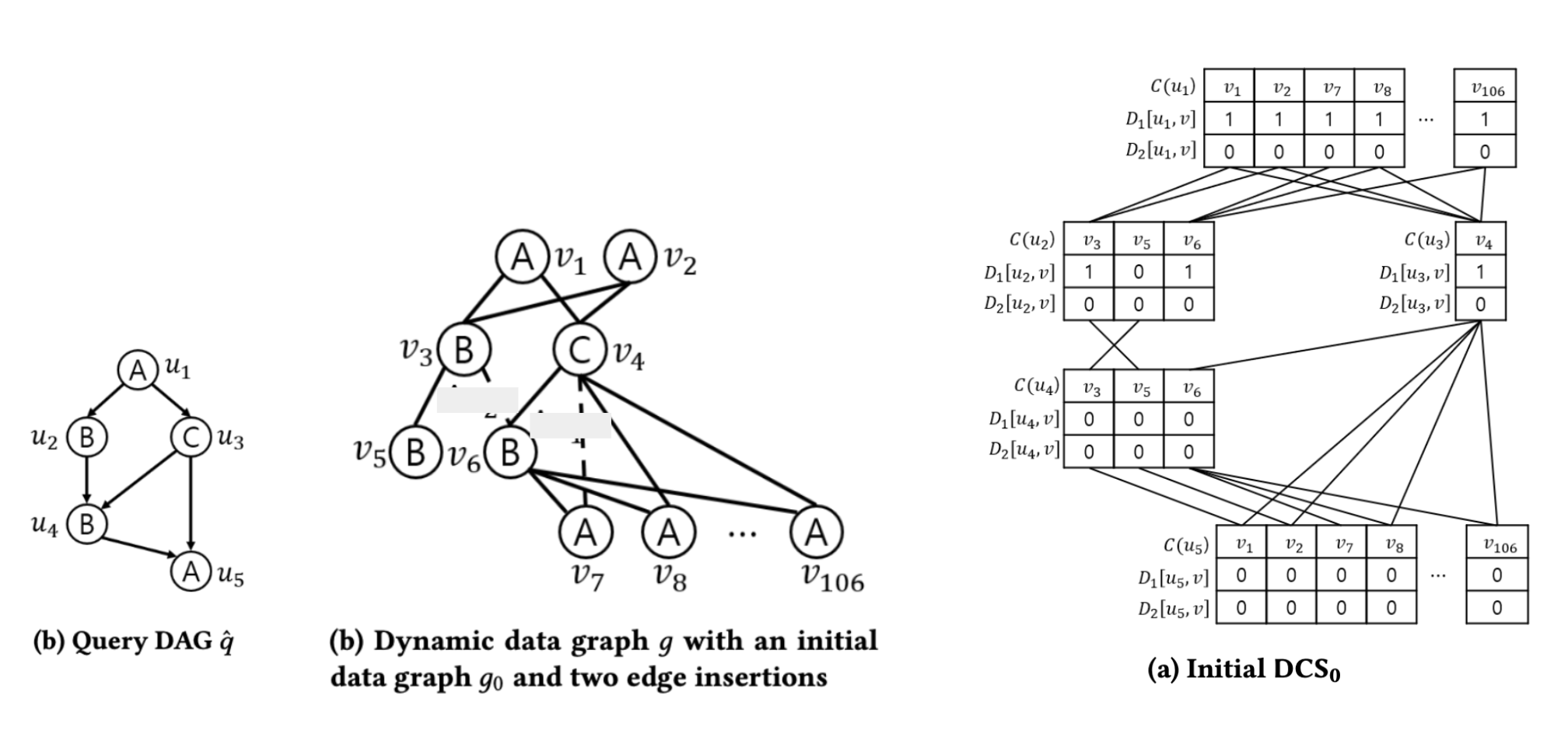
DCS에 Weak Embedding을 찾기 위해 계산하는 각종 중간 결과를 저장하고, 이를 바탕으로 Backtracking 탐색을 수행해 Weak Embedding을 찾게 됩니다.

지금은 그냥 형태만 살펴보는데, 행렬이 각 노드를 이루는 것을 볼 수 있습니다. 자세한 구성은 아래의 컴포넌트들의 정의를 이해하면서 설명 하겠습니다.

Candidate Set $C(u)$

쿼리 그래프의 노드 $u$와 데이터 그래프의 노드 $v$가 매칭이 가능한 노드 쌍을 모은 집합 입니다.

For each $u \in V(q)$, a set of vertices $v \in V(g)$ s.t.

\[l_q(u) = l_g(v)\]

, and represent a matching pair as $<u, v>$.

매칭이 가능한지 여부는 간단하게 두 노드의 레이블이 같다는 조건만 만족 하면 됩니다!

DCS only $C(u)$

이 $C(u)$를 정의하는 이유는 이것들을 가지고 DCS의 골격이 되는 노드를 정의할 수 있습니다.

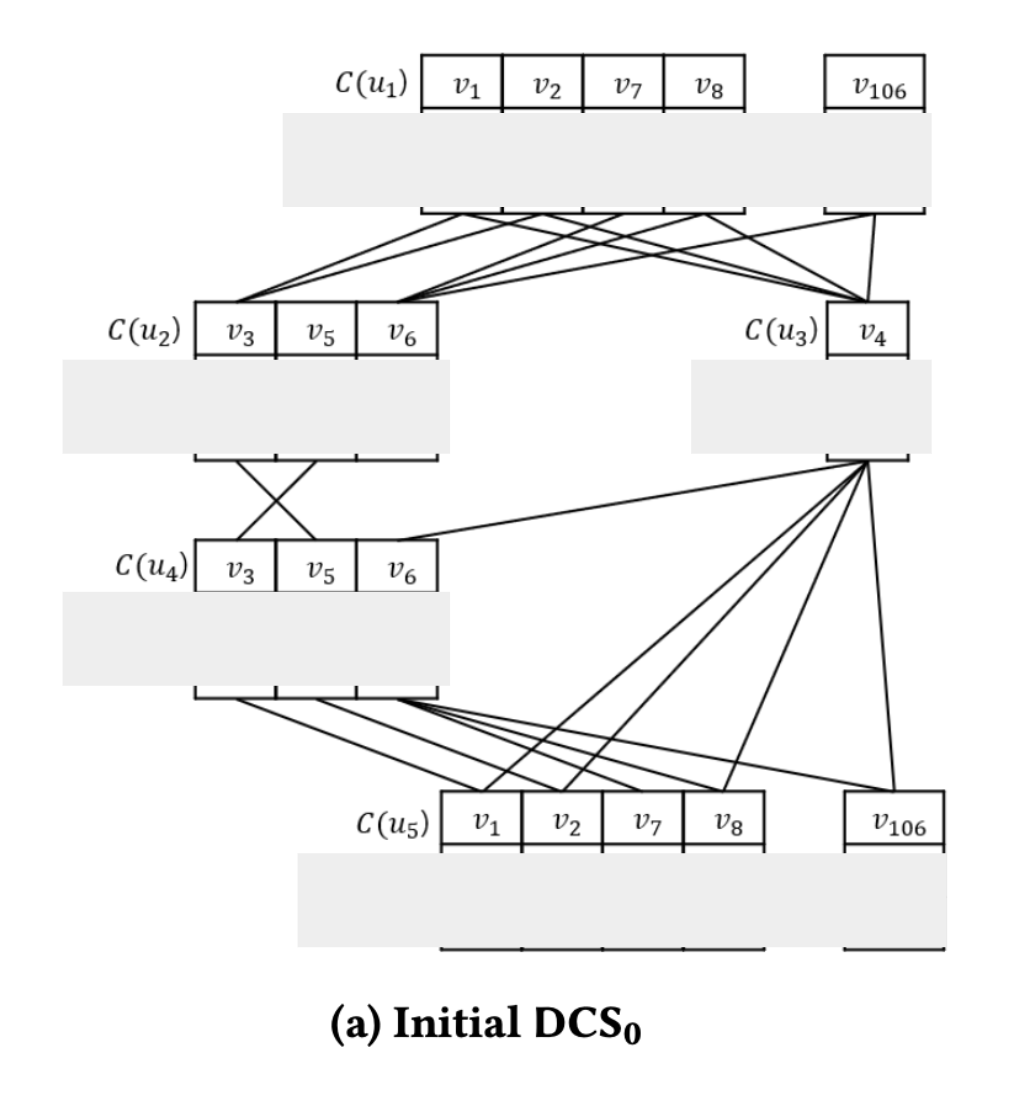
논문에서 다른 부분을 걷어내고, $C(u)$에 대한 부분만 표현한 그림 입니다.

이걸 만들어가는 과정을 따라가봅시다.

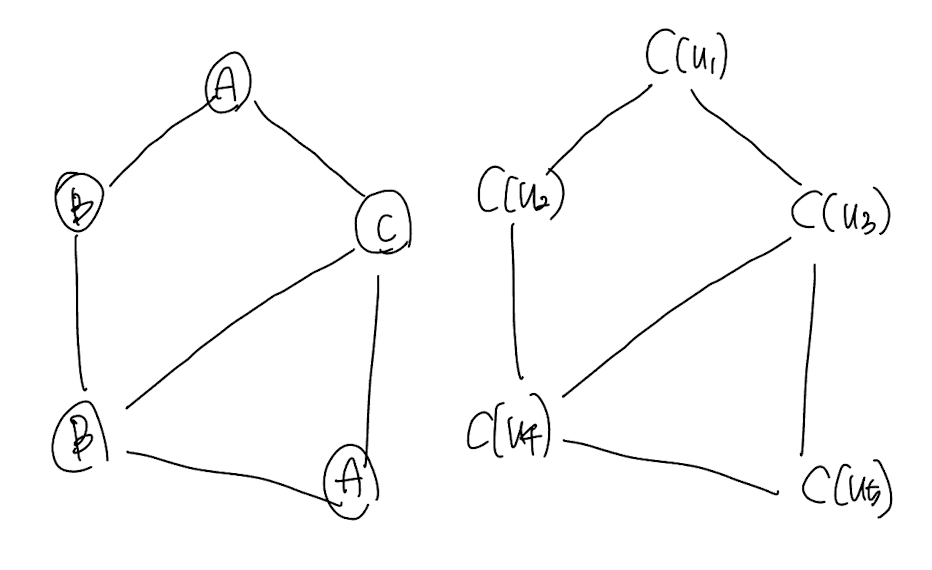
먼저, 기존의 쿼리 그래프 $q$에서 각 노드를 $C(u)$로 대체 해봅시다. 지금은 이해를 돕기 위해 연결 관계를 그려뒀는데요. DCS edge를 그리는 방법에 대해서 다루고 다면, 이것들을 지우고 어떻게 그리는 설명하겠습니다.

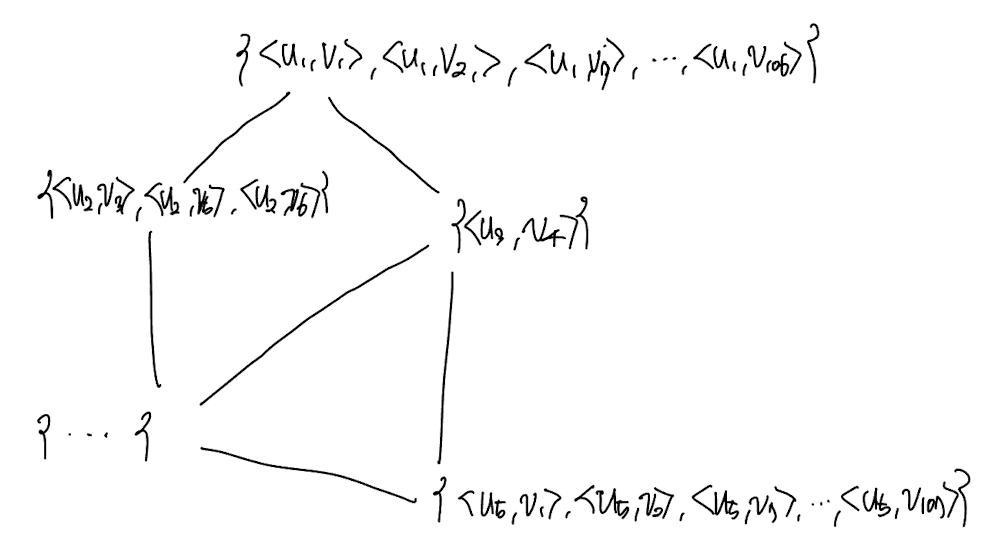
$C(u)$는 $<u, v>$의 집합으로 정의 했습니다. 이것 그대로 그래프로 표현하면 이렇게 될 것 입니다. 그런데, 보기가 너무 불편하고, 반복되는 부분도 많이 보입니다! 그래서 집합 표기 대신에 표의 형태로 표기를 바꿉니다.

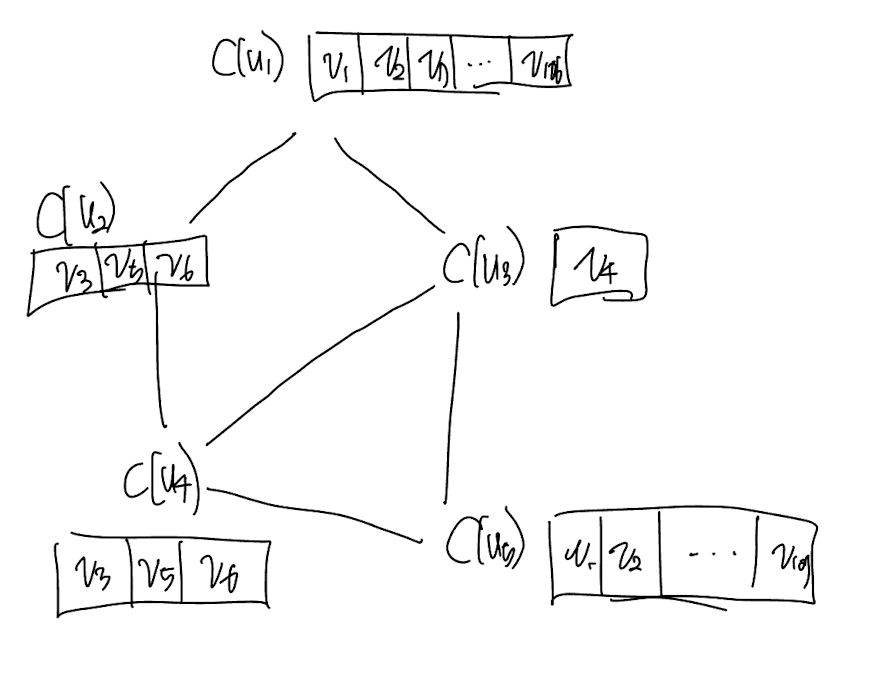
드디어! 논문에 나왔던 DCS 다이어그램과 비슷한 형태가 나왔습니다! ㅎㅎ 이제 DCS 그래프에서 엣지를 정의하는 방법에 대해 설명하겠습니다.

DCS Edges

DCS 상의 엣지는 두 $<u, v>, <u’, v’>$ 쌍이 연결 관계에 있음을 말합니다. 두 매칭 쌍이 연결 관계를 가지려면 아래의 조건을 만족해야 합니다.

• $(u, u’) \in E(q)$
• $(v, v’) \in E(g)$

즉, 매칭 쌍을 이루는 쿼리 노드 사이에도 연결성이 있어야 하고, 데이터 노드 사이에도 연결성이 있어야 합니다!

이제 기존에 가이드를 위해 그렸던, $C(u)$ 노드 사이의 연결성을 모두 지우고, DCS 엣지 정의에 맞춰서 DCS를 그려봅시다.

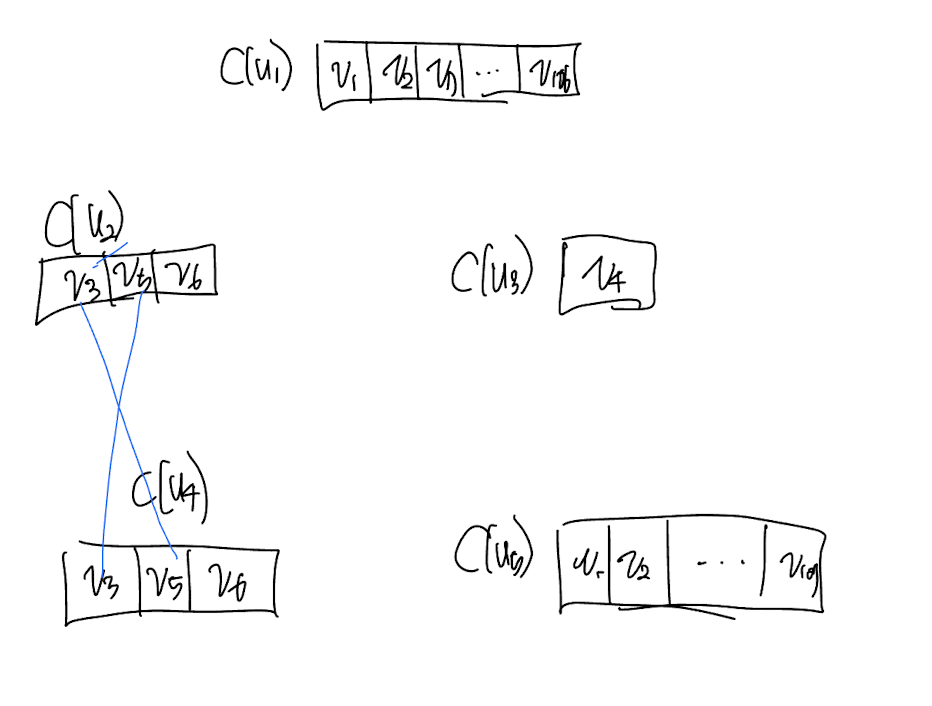
$B-B$ 엣지만을 찾아서 DCS 엣지를 그린 모습 입니다. 이때, $(u_2, u_4)$ 엣지에 방향성이 없다고 생각하고 엣지를 그려야 하기 때문에 저렇게 간선이 2개 생기는 것을 볼 수 있습니다.

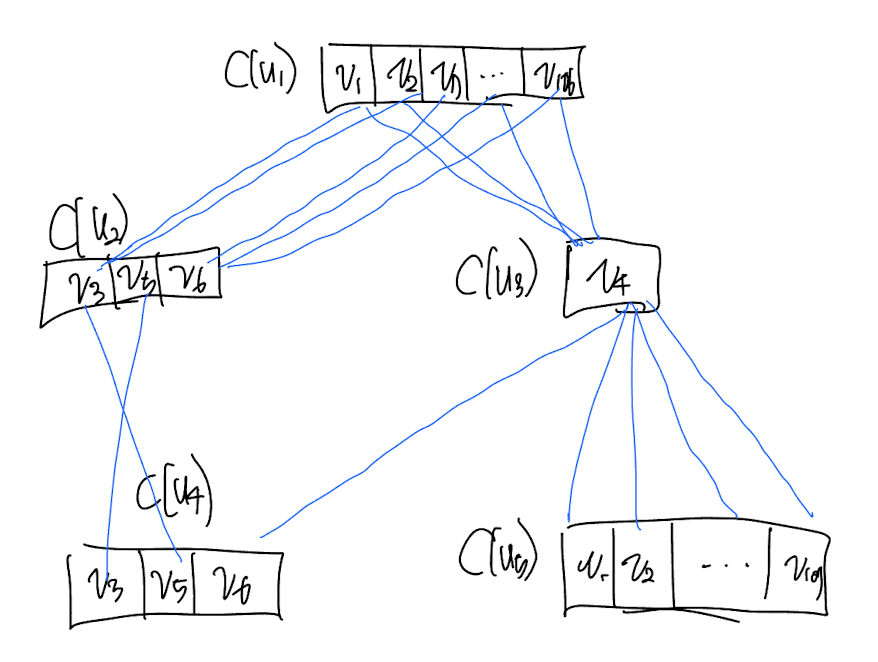
정의에 따라 모든 $(u, u’)$ 쌍에 대해 그릴 수 있는 DCS Edge를 찾아서 그려줍니다. 이때, 쿼리 그래프의 방향성이 없다고 생각하면서 엣지를 그려야 한다는 것에 주의 합니다.

정의에 맞게 모든 Edge를 그려주면 SymBi 논문에 나온 다이어그램을 얻을 수 있습니다.

하나 쉽게 발견할 수 있는 인사이트는,

만약 서로 연결된 두 쿼리 노드 $(u, u’) \in E(q)$에 대해서 $C(u)$와 $C(u’)$ 사이에 DCS 엣지가 하나도 없다면!
어떤 Subgraph Matching도 존재하지 않는다

고 말할 수 있습니다! 이것은 쿼리 그래프에서 있던 엣지 중 하나가 데이터 그래프에서 발견 되지 않는 상황이기 때문입니다.

그렇다고, 모든 쿼리 엣지 $(u, u’) \in E(q)$에 대해 $(C(u), C(u’)) \in E(\text{DCS})$라고 해서 Subgraph Matching이 존재하는 것은 아닙니다.

Subgraph Matching이 존재하기 위해선 추가적인 조건이 필요하며, 이 조건을 체크하여 저장하는 중간 자료구조가 앞으로 소개할 $D_0$, $D_1$, $D_2$ Matrix 입니다.

$D_0$ Matrix

주의! 이 $D_0$ Matrix는 SymBi 논문에는 등장하지 않는 자료구조 입니다! 제가 이해와 설명의 편의를 위해서 임의로 정의한 자료구조 입니다!

$D_0$ Matrix는 $<u, v>$ 매칭 쌍에 True/False 값을 부여한 행렬 입니다.

이 행렬은 쿼리 DAG $\hat{q}$에서 $u$를 root로 삼는 sub-DAG $\hat{q}_u$가 데이터 노드 $v$를 기준으로 Weak Embedding이 존재하는지 여부를 체크해 기록 합니다.

$D_0$ 값을 가장 구하기 쉬운 것들은 쿼리 DAG $\hat{q}$의 리프 노드를 이루는 쿼리 노드들입니다. 이들은 자식 노드들이 없기 때문에 자기 자신에 대해서만 체크하면 되기 때문입니다.

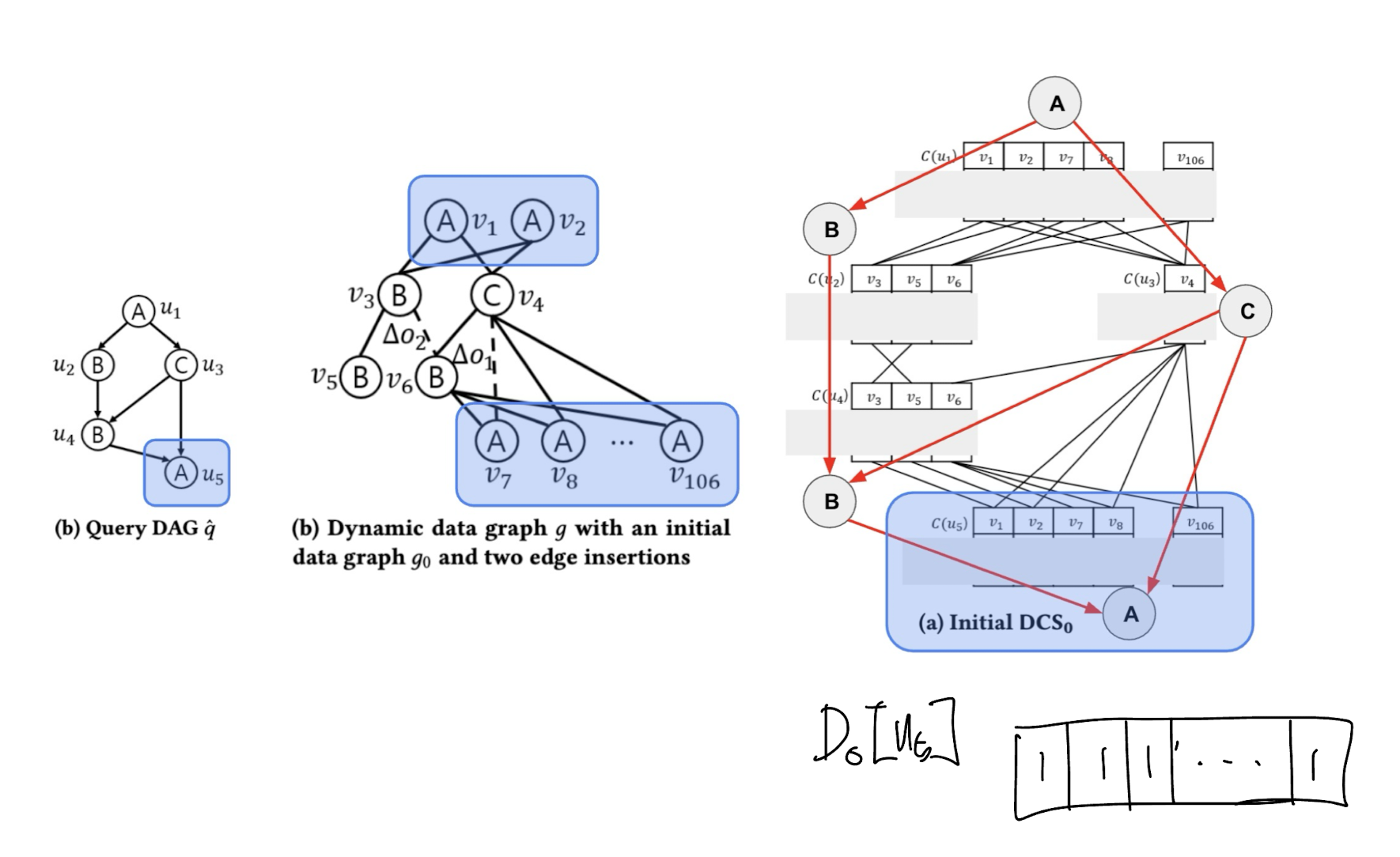
SymBi 논문의 쿼리 그래프를 기준으로 하면, $u_5(A)$ 노드가 리프 노드가 됩니다. 리프 노드는 자식 노드가 존재하지 않고, 따라서 sub-DAG $\hat{q}_{u_5}$에 대해 모든 서브 그래프 매칭이 존재한다고 판단 합니다. 그래서 $D_0[u_5]$ 값은 1로 채워집니다.

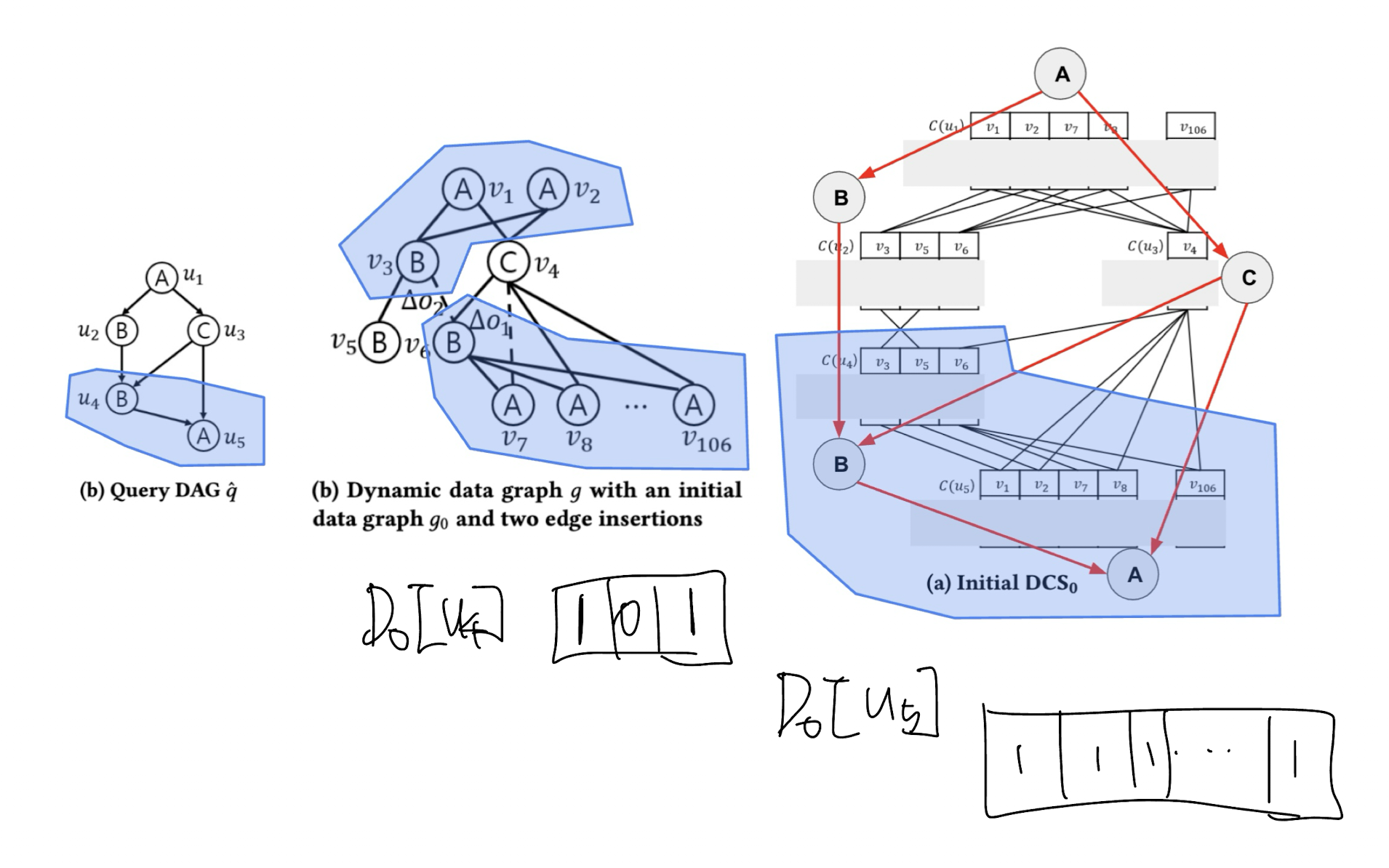
다음으로 sub-DAG $\hat{q}_{u_4}$에 대해서 살펴보겠습니다. 이 녀석은 데이터 노드 $v_3$를 루트로 하는 경우와 $v_6$를 루트로 하는 경우에 대해서 subgraph weak embedding이 존재합니다. 그래서 $D_0[u_4, v_3] = D_0[u_4, v_6] = 1$이 됩니다.

이때, $D_0[u, v] = 1$이 되는지 쉽게 판단하고 싶다면, $D_0[u, v]$와 연결된 DCS Edge $(<u, v>, <u’, v’>)$ 중에 $D_0[u’, v’] = 1$을 만족하는 DCS 노드가 적어도 하나 존재해야 합니다.

만약, (1) 연결된 DCS 노드가 없거나 (2) 연결된 DCS 노드 전부가 $D_0[u’, v’] = 0$이라면, $D_0[u, v] = 0$이 됩니다.

이걸 SymBi 논문에서 정의한 방식으로 옮겨 적으면 아래와 같습니다.

For each $u \in V(q)$ and $v \in V(g)$

• $D_0[u, v] = 1$ if there exists a weak embedding $M’$ of sub-DAG $\hat{q}_u$ at $v$.
• $D_0[u, v] = 0$ otherwise

이걸 코드로 작성하면 아래와 같을 것 입니다. 참고로 제가 임의로 작성한 것이기 때문에 실제 논문의 구현과는 다를 수 있습니다.

def fill_D0_matrix(u: QueryNode, v: DataNode):
  # Not DCS Node
  if not D0[u] or not D0[u][v]:
    return

  if isLeaf(u):
    D0[u][v] = 1

  for dcs_c in DCS[u][v].children():
    u_c, v_c = dcs_c
    if D0[u_c][v_c]:
      # if there exist, D0 mapping
      D0[u][v] = 1
      return

  D0[u][v] = 0

이때, fill_D0_matrix(u, v) 함수는 리프 노드부터 시작해 그들의 부모 노드 순서대로 올라가며 호출해야 됨을 유의하자.

$D_1$ Matrix

$D_1$ Matrix도 $D_0$ Matrix와 동일하게 $<u, v>$ 매칭 쌍에 True/False 값을 부여한 행렬 입니다.

하지만, 이 행렬은 쿼리 DAG $\hat{q}$가 아닌 역방향 DAG인 $\hat{q}^{-1}$를 기준으로 Weak Embedding이 존재하는지 여부를 체크해 기록 합니다.

이걸 쉽게 풀어서 적으면,

• $D_0$는 “순방향 DAG“를 기준으로 작성하기 때문에
  • “자식 노드“들에 대해 Weak Embedding이 존재하는지 판단한 중간 결과이고,
• $D_1$은 역방향 DAG를 기준으로 작성하기 때문에
  • “부모 노드“들에 대해 Weak Embedding이 존재하는지 판단한 중간 결과입니다.

$D_0$에서는 쿼리 DAG $\hat{q}$의 리프 노드부터 값을 채워나갔습니다. $D_1$는 반대로 쿼리 DAG $\hat{q}$의 루트 노드부터 값을 채우면 됩니다.

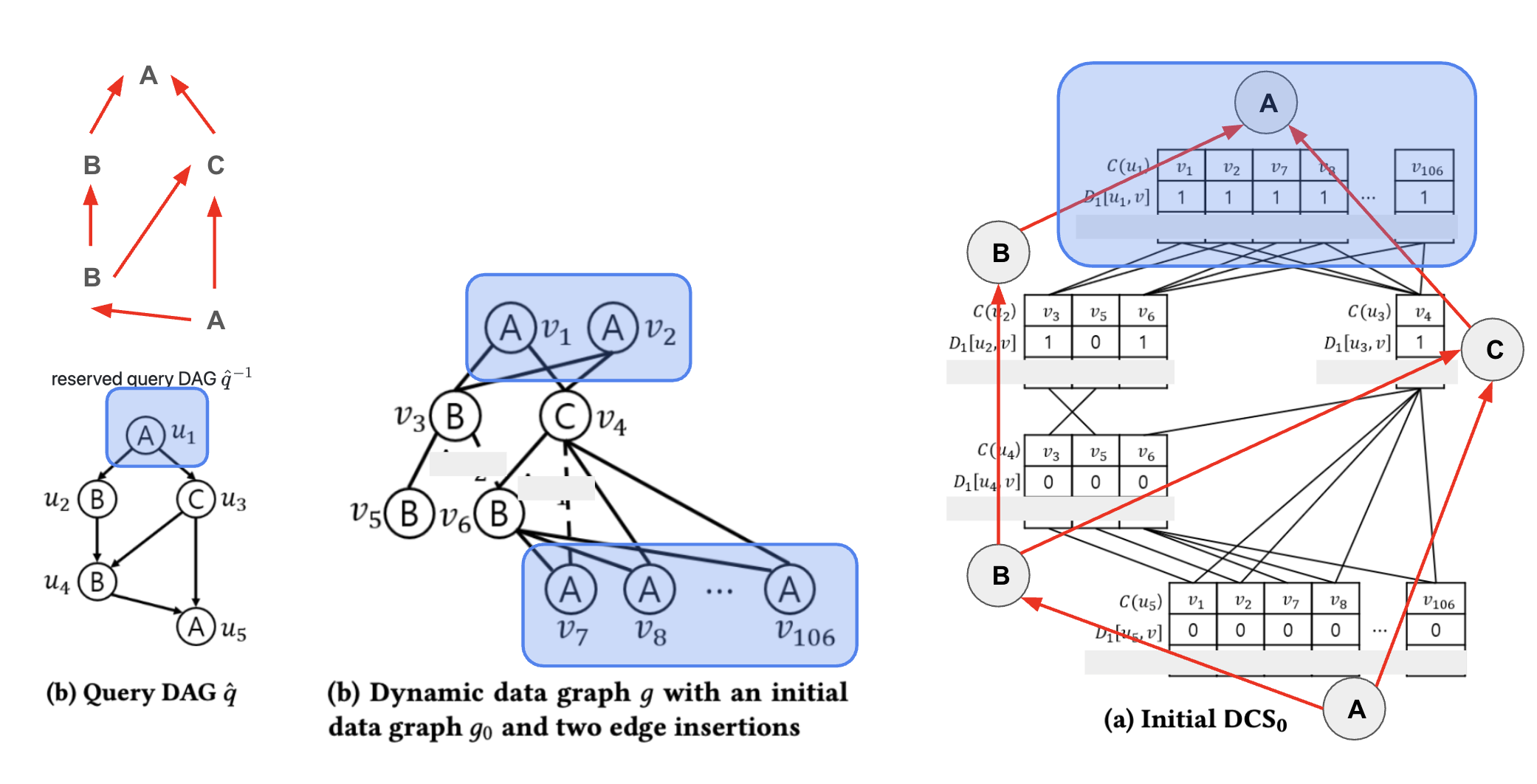
루트 노드인 $u_1$에 대해 역방향 DAG $\hat{q}^{-1}_{u_1}$에서의 subgraph weak embedding은 항상 존재합니다. 따라서, 모든 $D_1[u_1]$은 1로 채워집니다.

이걸 순방향 DAG의 루트노드부터 자식 노드들 순서로 $D_1$을 계산하면서 채워나가면 됩니다. 그러면 아래와 같이 $D_1$ 값이 채워진 DCS 그래프를 얻을 수 있습니다.

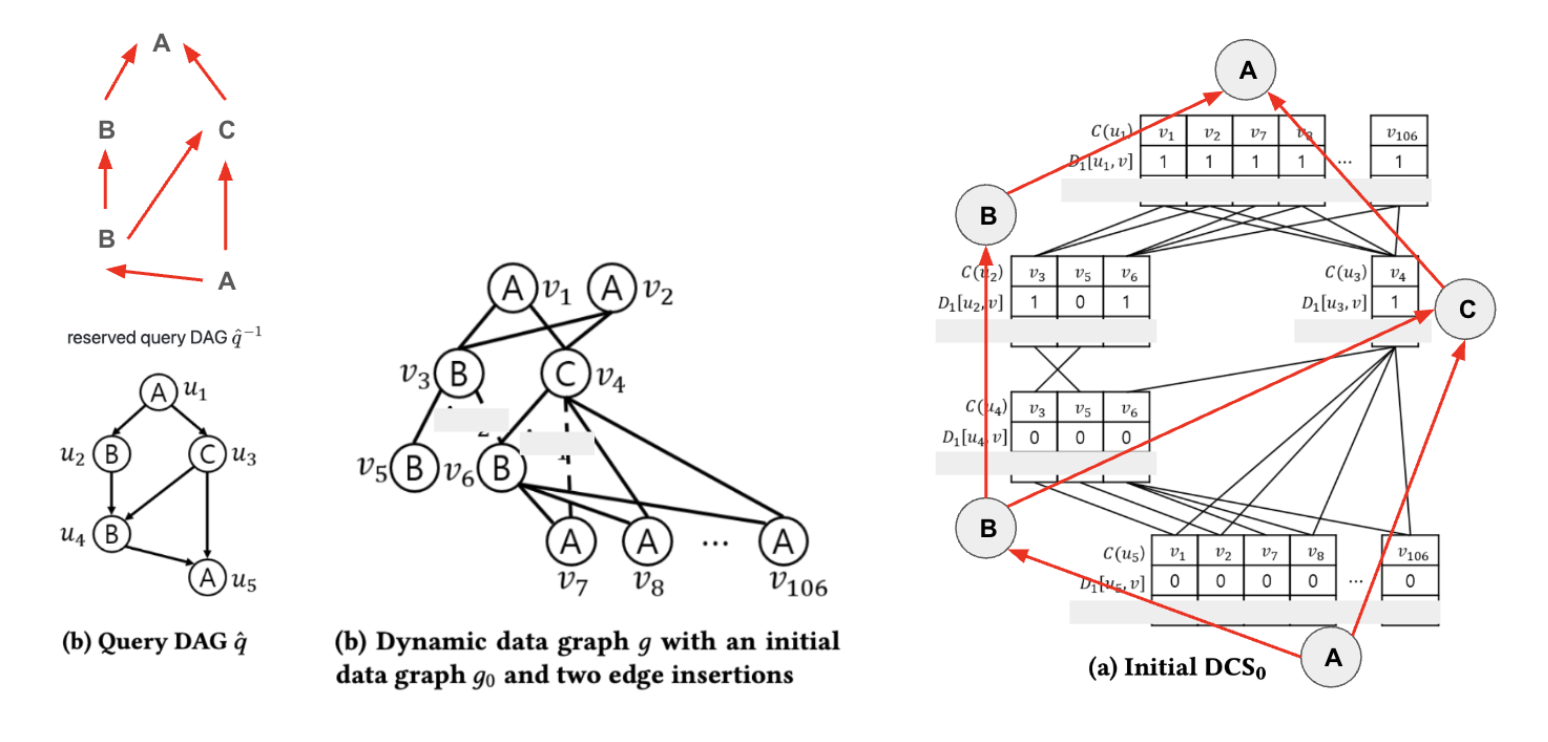
이걸 SymBi 논문에서 정의한 방식으로 옮겨 적으면 아래와 같습니다.

For each $u \in V(q)$ and $v \in V(g)$

• $D_1[u, v] = 1$ if there exists a weak embedding $M’$ of sub-DAG $\hat{q}^{-1}_u$ at $v$.
• $D_1[u, v] = 0$ otherwise

마찬가지로 python 코드로 구현해보면 아래와 같을 것 같습니다.

def fill_D1_matrix(u: QueryNode, v: DataNode):
  # Not DCS Node
  if not D1[u] or not D1[u][v]:
    return

  if isRoot(u):
    D1[u][v] = 1

  for dcs_c in DCS[u][v].parent():
    u_c, v_c = dcs_c
    if D1[u_c][v_c]:
      # if there exist, D1 mapping
      D1[u][v] = 1
      return

  D1[u][v] = 0

$D_2$ Matrix

마지막으로 $D_2$ Matrix 입니다. $D_2$는 Subgraph Matching을 찾기 위해 직접적으로 사용하는 자료구조이기 때문에 중요한 녀석 입니다.

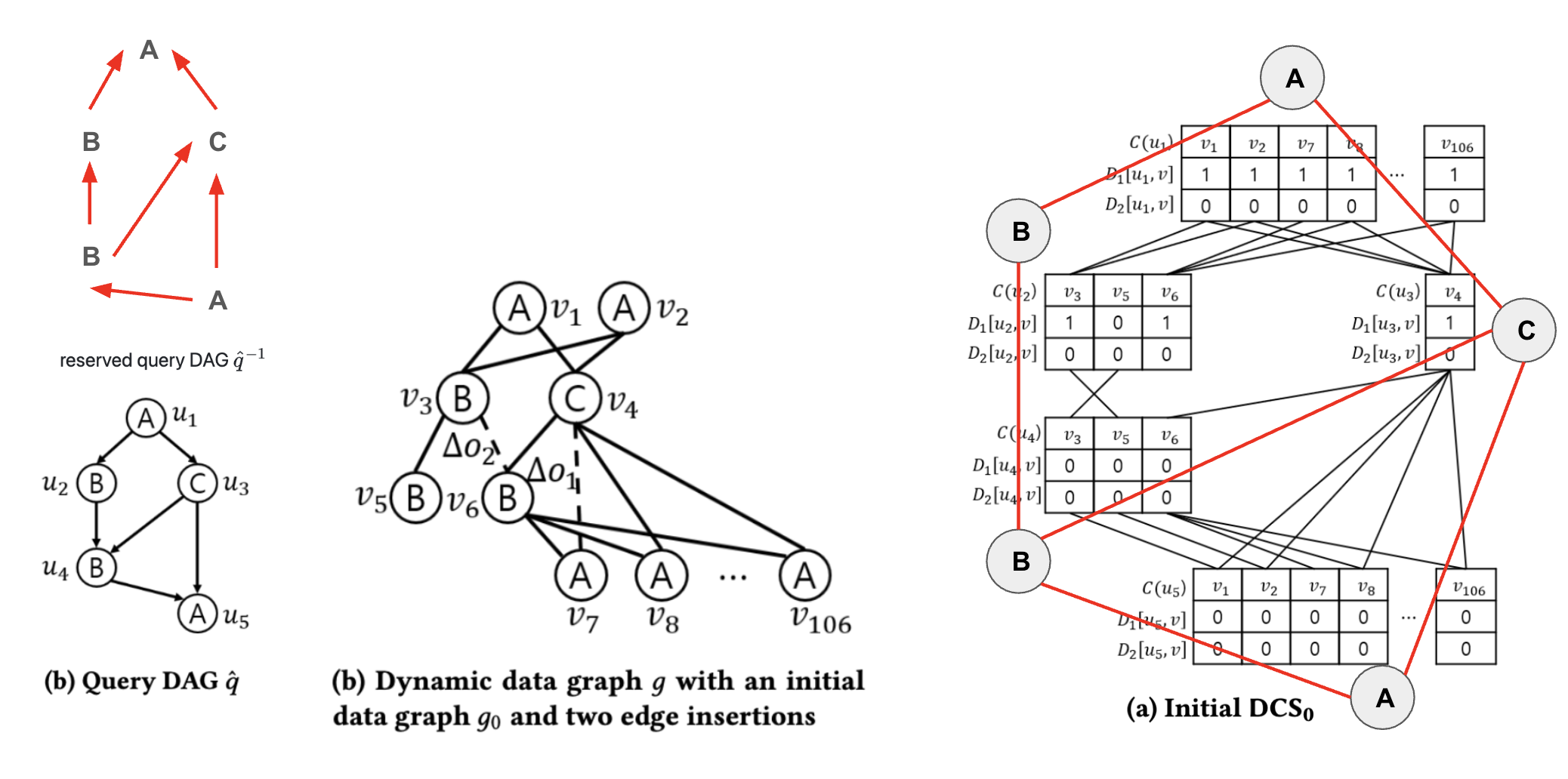
$D_2$는 순방향 DAG $\hat{q}$를 기준으로 작성하는 값 입니다. $D_0$랑 비슷하죠. 하지만 추가적인 조건이 들어갑니다. 바로

1. $D_1[u, v] = 1$
   1. $D_2$를 평가하는 바로 그 지점 $<u, v>$에서 parent subgraph mapping이 존재해야 한다.
2. For every child $u_c$ of $u$ in $\hat{q}$, there exist $v_c$ s.t. adjacent to $v$ and $D_2[u_c, v_c] = 1$.

저는 $D_2$가 좀 이해하기 어려워서 $D_0$라는 논문에 없는 녀석을 추가로 만들었습니다. 저는 $D_2[u, v] = 1$이 되기 위해서는 적어도 $D_0[u, v] = D_1[u, v] = 1$이 되어야 한다고 생각 했습니다.

이것은 $<u, v>$에 대해서 child subgraph 매핑도 존재하고, parent subgraph 매핑도 존재해야 우리가 원래 찾고자 했던 Weak Embedding이 존재하는 최소 조건이라고 생각했기 때문입니다.

하지만, 추가 조건을 넣어서 저는 아래와 같이 정의하였습니다. (제 정의이므로 틀린 수도 있습니다.)

1. $D_1[u, v] = D_0[u, v] = 1$을 만족하고
2. 모든 부모 노드에 대해서, $D_1[u_p, v_p] = D_0[u_p, v_p] = 1$를 만족하고
3. 모든 자식 노드에 대해서, $D_1[u_c, v_c] = D_0[u_c, v_c] = 1$를 만족한다면

$D_2[u, v ] = 1$이 된다.

Find Subgraph Matching

이제 DCS 자료구조를 이루는 $C(u)$, $D_1$, $D_2$ 값을 모두 구성 했으니, 자료 구조 초기화를 완료한 것 입니다! (야호!)

이제 이 DCS 자료 구조에서 Subgraph Matching을 찾는 방법에 대해 살펴보겠습니다.

방법은 단순한 Graph 탐색을 하면 됩니다. 그런데, 이때 탐색하는 DCS 노드의 $D_2[u, v] = 1$을 만족해야 합니다. 우리는 $D_2[u, v] = 1$을 만족하는 노드만 탐색할 것 입니다.

$D_2[u, v] = 1$을 만족하는 DCS 노드만 모아서 backtracking을 한다고 보면 됩니다. 그래프 탐색을 했는데, 전체 $V(q)$를 순회할 수 있다면, 그럼 Subgraph Matching이 존재하는 것 입니다!

맺음말

이어지는 포스트에서는 업데이트 스트림 $\Delta o_i$가 들어올 때, 구축한 DCS 자료구조의 $D_1$, $D_2$ 값을 어떻게 업뎃 하는지 살펴보겠습니다.

➡️ Symbi, Update DCS

보충

제가 논문을 읽으면서 계속 헷갈렸어서 메모를 남겨둡니다.

“DCS 그래프의 노드는 $<u, v>$ 입니다”. Symbi 논문의 다이어그램과 제가 설명을 할 때, $C(u)$가 노드인 것처럼 설명하거나, $C(u), D_1[u], D_2[u]$가 함께 있는 표가 DCS 그래프의 노드인 것처럼 설명했지만, 본질을 본다면, $<u, v>$가 DCS의 노드 입니다.

그리고 DCS 상에서 부모 노드라고 한다면, $<u_p, v_p>$가 $<u, v>$ 노드의 부모 노드라는 것 입니다. 이것은 $(u_p, u) \in E(q)$이고, $\hat{q}$에서는 $u_p$가 $u$의 부모노드라는 것입니다. $(v_p, v) \in E(g)$인데, 데이터 노드 사이에는 그냥 연결성만 있으면 됩니다.