Paper Reading: SymBi, Update DCS

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

How to Update DCS

이전 포스트에서 DCS 자료구조를 구성하고 값들을 셋업 하는 방법에 대해서 살펴보았습니다. (길다길어…)

본래 SymBi에서 푸려고 하는 문제는 Update Stream $\Delta o_i$가 존재하는 CSM 문제 입니다.

$\Delta o_i$는 삽입과 삭제가 가능하지만, 삽입 과정을 제대로 이해하면 삭제 과정은 쉽게 구현할 수 있기 때문에 이 포스트에서는 삽입 과정에 대해서만 기술하겠습니다. 앞으로의 모든 Update Stream은 모두 엣지 삽입 업뎃 입니다.

DCS Change Edge

Insert Stream $\Delta o_i$로 인해서 서로 연결되지 않았던 DCS 노드가 연결될 수 있습니다. 이렇게 연결되는 DCS Edge의 집합 $E_{\text{DCS}}$를 찾아내는 것이 첫번째로 할 일 입니다.

1. Get newly inserted edge $e = (v, v’)$.
2. Traverses the query graph $q$ and find an edge $(u, u’)$ s.t.
   1. $l_q(u) = l_g(v)$ and
   2. $l_q(u’) = l_g(v’)$
3. Insert the edge $(<u, v>, <u’, v’>)$ into the set $E_{\text{DCS}}$.

Update $D_1$

Edge Insert로 추가된 DCS Edge의 집합 $E_{\text{DCS}}$를 얻었고, 이제 이를 바탕으로 DCS의 $D_1$, $D_2$ 값을 업데이트 해야 합니다.

$E_{\text{DCS}}$에서 DCS 엣지 하나 $(<u_p, v_p>, <u, v>)$를 골라서 과정을 따라가봅시다. 이때 케이스가 2가지로 나뉘는데,

[$D_1[u_p, v_p] = 0$]

이 경우는 Parent Node에서 Parent Subgraph Matching이 존재하지 않는 경우 입니다.

이때는 $(<u_p, v_p>, <u, v>)$ 사이에 연결이 생겨도 Parent DCS Node에 대해서 Subgraph Matching이 성립되지 않을 것이라는 말 입니다.

그래서 $D_1$ 업데이트 과정을 종료 합니다.

[$D_1[u_p, v_p] = 1$]

이 경우는 Parent DCS Node에 대해 Subgraph Matching이 존재하는 경우 입니다!

이때는 업뎃으로 인해서 $D_1[u, v]$의 값이 0에서 1로 바뀔 여지가 있습니다. 그래서 $D_1[u, v]$의 값을 다시 계산합니다. 우리는 $<u, v>$의 부모 중 하나인 $<u_p, v_p>$에 대해서는 $D_1$ 값이 1인 것을 확인했으니, 나머지 다른 부모 $<u_p’, v_p’>$ 모두에 대해서 $D_1[u_p’, v_p’] = 1$를 만족하는지를 체크하면 됩니다.

만약, 업뎃으로 인해 $D_1[u, v]$ 값이 0에서 1로 바뀌었다면, $<u, v>$의 모든 자식 노드들도 $D_1$ 값이 바뀔 여지가 있습니다. 그래서 $D_1$ 재계산 과정을 모든 자식 모드에 대해서도 수행해줍니다. (재귀)

Side-effect

그런데, 여기에서 연산을 덜어낼 수 있는 부분이 존재합니다!

일단 이 방법은 $D_1[u, v]$을 재계산 하기 위해, 이번 업데이트에서 변화가 없었던 나머지 부모 전부의 $D_1[u_p, v_p]$ 값을 확인해야 합니다. 만약, 이 DCS 노드에 $N$개 Parent가 있었다면, 매번 $O(N)$의 연산이 들게 됩니다.

만약, 업데이트 스트림에 의해 $<u, v>$의 부모에 대해 $M$번의 업데이트가 발생 했다면, 위의 과정을 최대 $M$번 반복해야 합니다. (단, $D[u_{pi}, v_{pi}] = 0$인 상황이라면, $D_1[u, v]$ 업데이트도 발생하지 않는 것에 유의 합니다.)

결국 $D_1[u, v]$ 값을 업뎃 하기 위해서 그것의 모든 부모에 대한 값 참조가 발생하고 이로 인해, 최대 $O(MN)$의 계산 코스트가 든다는 것 입니다.

논문에서는 이 계산 코스트를 줄이기 위해 추가정보를 저장하는 중간단계 자료구조를 도입 합니다!

Improved Updating

$D_1[u, v]$의 값을 업뎃하는 상황을 떠올려봅시다. 이 값이 $D_1[u, v] = 0 \rightarrow 1$로 바뀌는 순간은 모든 부모 노드 $u_p$에 대해서 $D_1[u_p, v_p] = 1$인 $v_p$가 존재할 때 입니다.

이것은 $D_1[u, v]$의 값이 아래와 같이 계산될 수 있음을 말합니다.

# 설명을 위해 임의로 작성한 코드 입니다.
num_parent = get_parent(u)  # O(1)
num_D1_parent = get_d1_parent(u, v)  # O(N * |C(u_p)|)

D1[u][v] = (num_parent == num_D1_parent)

• get_parent(u)는 그래프 정보를 잘 저장해뒀으면 $O(1)$으로 가능하지만,
• get_d1_parent(u, v)는 DCS 그래프를 순회해야 하므로, $O(N \times |C(u_p)|)$ 만큼이 필요 합니다.

D1 Parents Array $N^1_P[u, v]$

그래서 Symbi에서는 get_d1_parent(u, v)를 빠르게 계산하기 위해 $N^1_P[u, v]$ 자료구조를 도입 합니다. 이 자료구조는 DCS 부모 중에서 $D_1[u_p, v_p] = 1$인 $v_p$가 존재하는, 부모 노드의 갯수를 저장하는 배열 입니다. 그럼 코드가 아래와 같이 바뀝니다.

# 설명을 위해 임의로 작성한 코드 입니다.
num_parent = get_parent(u)  # O(1)
num_D1_parent = N1P[u][v]  # O(1)

D1[u][v] = (num_parent == num_D1_parent)

그런데, 이 $N^1_P[u, v]$를 어떻게 구할 수 있을까요? 일단 DCS 자료구조가 셋업 되어 있다면, $N^1_P[u, v]$의 정의를 따라 계산해주면 됩니다. $N^1_P[u, v]$를 구하는 순서도 상관 없습니다.

DCS 그래프에 $(<u_p, v_p>, <u, v>)$ 엣지가 추가로 연결 되었습니다. 그러면, $N^1_P[u, v]$의 값이 업데이트될 여지가 있습니다!

• 만약 $D_1[u_p, v_p] = 0$ 이라면,
  • $N^1_P[u, v]$ 증감이 발생하지 않습니다.
• 만약 $D_1[u_p, v_p] = 1$ 이라면,
  • $D_1[u_p]$에 대해서 $D_1[u_p, v_p] = 1$이 Parent subgraph mapping을 처음 만족하는 녀석이었나?
    • 그러면 $N^1_P[u, v]$의 값을 1 올려줍니다.
    • 그리고 $D_1[u, v]$ 값도 재계산이 필요합니다.
  • 이미 $D_1[u_p]$에서 Parent subgraph mapping을 만족하던 다른 $v_p’$가 있었다면,
    • 그건 $N^1_P[u, v]$에 이미 반영 되어 있습니다. 값 변화가 발생하지 않습니다.
    • 마찬가지로 $D_1[u, v]$의 값도 변화가 없습니다.

그러나, 여기에서도 여전히 개선할 부분이 존재합니다! 바로 $D_1[u_p]$에 대해서 이게 처음으로 Parent subgraph mapping을 만족하는 녀석이었는지, 아님 기존에 Parent subgraph mapping을 만족하던 녀석이 있었는지 확인하는 과정에서 $O(| C(u_p) |)$ 만큼 계산 비용이 듭니다.

D1 Parent Candidates Array $N^1_{PC}[u, v, u_p]$

논문에서는 \(N^1_{PC}[u, v, u_p]\)가 아니라 $N_{u, v}^1[u_p]$라고 표기하지만, 저는 표기가 너무너무 헷갈려서 여기서는 새로운 표기로 작성하겠습니다. 내 마음임대로 ㅋㅋ $PC$는 Parent Candidate의 약자 입니다.

SymBi는 이걸 $O(1)$ 시간 만에 판단하기 위해서 추가 자료구조 $N^1_{PC}[u, v, u_p]$를 도입 합니다. (그만…)

이것은 $<u, v>$의 부모 노드 $<u_p, v_p>$가 있을 때, $D_1[u_p, v_p] = 1$을 만족하는 $v_p$의 갯수를 저장하는 자료구조 입니다.

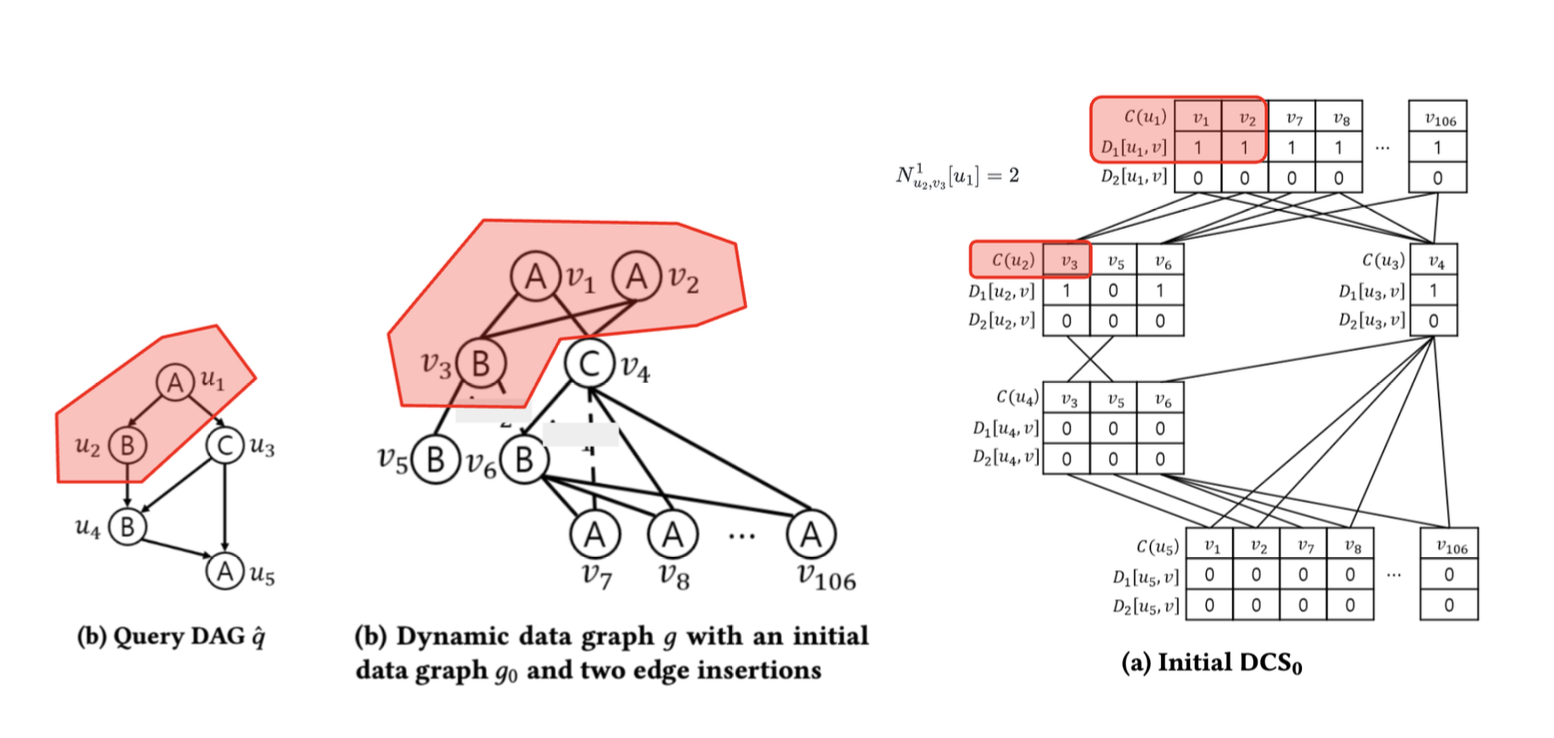
예시를 통해 \(N^1_{PC}\)을 이해해봅시다. DCS의 노드 $<u_2, v_3>$와 그것의 부모 노드 $<u_1, v_p>$가 있습니다. 이때, $D_1[u_1, v_p] = 1$을 만족하는 $v_p$가 2개 있으므로 $N^1_{PC} = 2$가 됩니다!

이 정보가 있다면, \(N^1_P[u, v]\)의 값을 $N^1_{PC}[u, v, u_p]$ 값이 0에서 1로 바뀔 때만 증가시키면 됩니다! (얏호!)

만약 \(N^1_{PC}[u, v, u_p]\) 값이 여전히 0이거나, $N^1_{PC}[u, v, u_p]$ 값이 이미 1 이상인 상태에서 $D_1[u_p, v_p] = 1$인 $v_p$가 추가되는 거라면, $N^1_P[u, v]$도 $D_1[u, v]$도 값 변경이 발생하지 않습니다.

DCS 그래프에 $(<u_p, v_p>, <u, v>)$ 엣지가 연결되는 경우 어떻게 $N^1_P$, \(N^1_{PC}\) 값이 업데이트 되는지 다시 살펴봅시다.

• 만약 $(<u_p, v_p>, <u, v>)$ 엣지가 이미 있었다면,
  • 이미 $N^1_{PC}, N^1_P, D_1$에 반영 되어 있습니다. 중복 계산할 필요 없고, 종료 합니다.
• 만약 $D_1[u_p, v_p] = 0$ 이라면,
  • $N^1_{PC}[u, v, u_p]$에 값 증감이 발생하지 않습니다.
  • $N^1_P[u, v]$ 증감이 발생하지 않을 것이니, 과정을 종료 합니다.
• 만약 $D_1[u_p, v_p] = 1$ 이라면,
  • $N^1_{PC}[u, v, u_p]$에 값을 1 증가 시킵니다.
  • 그런데, 이게 0에서 1로 바뀌는 경우라면?
    • 그러면 $N^1_P[u, v]$의 값을 1 올려줍니다.
    • 그리고 $D_1[u, v]$ 값도 재계산 합니다.
  • 그게 아니라면 과정을 종료 합니다.

이 과정을 살펴보면 더이상 $C(u_p)$ 집합을 순회하지 않습니다. 따라서 $D_1$ 업데이트에 $O(1)$ 상수 시간만 걸리게 됩니다! 그리고 $N^1_P$, \(N^1_{PC}\)도 상수 시간으로 업뎃 됩니다!

D2 Child Array $N^2_C$

$D_1$을 상수시간으로 계산하기 위해 추가 자료구조를 도입 했듯, 마찬가지로 $D_2$에 대해서도 추가 자료구조를 도입 합니다.

이것은 $D_2$에 대해서도 $D_2[u, v] = 0 \rightarrow 1$로 바뀌는 순간은 모든 자식 노드 $u_c$에 대해서 $D_2[u_c, v_c] = 1$인 $v_c$가 존재할 때 입니다.

# 설명을 위해 임의로 작성한 코드 입니다.
num_child = get_child(u)  # O(1)
num_D1_child = get_d2_child(u, v)  # O(N * |C(u_c)|)

D2[u][v] = (num_child == num_D2_child) and D1[u][v]

$D_2[u, v]$는 $D_1[u, v] = 1$인지도 체크해야 한다는 것도 유의 합니다.

get_d2_child(u, v) 값을 빠르게 구하기 위해서 $N^2_C[u, v]$ 자료구조를 도입 합니다. 이 자료구조는 DCS 자식 중에서 $D_2[u_c, v_c] = 1$인 $v_c$가 존재하는, 자식 노드의 갯수를 저장하는 배열 입니다.

# 설명을 위해 임의로 작성한 코드 입니다.
num_child = get_child(u)  # O(1)
num_D1_child = N2C[u][v]  # O(1)

D2[u][v] = (num_child == num_D2_child) and D1[u][v]

그런데, $N^2_C[u, v]$를 계산하는 과정에서 $O(|C(u_c)|)$ 만큼의 계산 비용이 들고, 이를 상수 시간으로 바꾸기 위해 (같은 방식으로) 추가 자료구조를 도입 합니다.

D2 Child Candidate Array $N^2_{CC}$

논문에서는 \(N^2_{CC}[u, v, u_c]\)가 아니라 $N_{u, v}^2[u_c]$라고 표기하지만, 저는 표기가 너무너무 헷갈려서 이 부분도 저만의 표기로 작성하겠습니다. $CC$는 Child Candidate의 약자 입니다.

이 자료구조는 $<u, v>$의 자식 노드 $<u_c, v_c>$가 있을 때, $D_2[u_c, v_c] = 1$을 만족하는 $v_c$의 갯수를 저장하는 자료 구조 입니다.

마찬가지로 이 정보가 있다면, $N^2_C[u, v]$의 값을 \(N^2_{CC}[u, v, u_c] = 0 \rightarrow 1\)가 될 때만 증가시키면 됩니다.

전체를 정리하면, DCS 엣지 추가 업데이트인 $(<u, v>, <u_c, v_c>)$가 있을 때 $N^2_C[u, v]$, \(N^2_{CC}[u, v, u_c]\)는 이렇게 업데이트 됩니다.

• 만약 $(<u, v>, <u_c, v_c>)$ 엣지가 이미 있었따면,
  • 이미 \(N^2_{CC}\), $N^2_C$, $D_2$에 반영 되어 있습니다. 과정을 종료 합니다.
• 만약 $D_2[u_c, v_c] = 0$이라면,
  • 추가 자료구조들에 값 증감이 발생하지 않습니다. 과정을 종료 합니다.
• 만약 $D_2[u_c, v_c] = 1$이라면,
  • \(N^2_{CC}[u, v, v_c]\) 값을 1 증가 시킵니다.
  • 그런데, 이게 0에서 1로 바뀌는 경우라면?
    • 그러면 $N^2_C[u, v]$의 값을 1 올려줍니다.
    • 그리고 $D_2[u, v]$의 값도 재계산 합니다.
  • 그게 아니라면 과정을 종료 합니다.

Review the process with Paper

지금까지 제 방식으로 각 자료구조가 왜 필요한지, 그리고 업데이트가 있을 때 DCS 값이 어떻게 바뀌는지 설명했는데요! Symbi 논문에서는 이것을 알고리즘 코드로도 제시해줍니다! 각 알고리즘 코드와 비교하며 다시 살펴봅시다.

1. 일단 $D_1[u_p, v_p] = 1$이어야 다음 과정이 진행 됩니다. [A2-L5]
2. \(N^1_{PC}[u_c, v_c, u] = 0\)이어야 $0 \rightarrow 1$로 증가하는게 되고, $N^1_P$ 값 증가가 가능합니다. 그래서 이를 체크 합니다. [A3-L1]
3. $N^1_P$ 값을 1 증가 시킵니다. [A3-L2]
4. 만약 $N^1_P$ 값이 $u_c$의 부모 쿼리 노드 갯수와 같은지 체크 합니다. [A3-L3]
5. 같다면 $D_1$ 값을 업뎃 합니다. [A3-L4]
6. 이때, $N^2_C[u_c, v_c]$에 대해서 $D_2 = 1$이 될 조건을 갖추고 있었는데, $D_1[u_c, v_c]$가 0이라서 $D_2 = 0$인 상황이었다면, $D_2[u_c, v_c] = 1$로 업데이트 해줍니다.

표기들을 다 이해한 후에는 논문의 알고리즘이 쏙쏙 이해된다 (아마도… ㅋㅋ)

이어서 $D_2$ 값이 업데이트 되는 과정도 살펴보자.

1. 일단 $D_2[u_c, v_c] = 1$이어야 다음 과정이 진행 됩니다. [A2-L7]
2. \(N^2_{CC}[u_p, v_p, u] = 0 \rightarrow 1\)인 상황이어야 $N^2_C$ 값 증가가 가능 합니다. [A4-L1]
3. 그리고 $D_2$를 업뎃 하기 위해 $D_1$와 $N^2_C$ 값이 자식 쿼리 노드 갯수와 같은지 체크 합니다. [A4-L3]
4. 같다면, $D_2$ 값을 업뎃 합니다. [A4-L4]

[A2-L9] 부분은 InsertionBottomUp() 함수의 호출로 인해 부모 노드의 $D_2[u_p, v_p] = 0 \rightarrow 1$가 된 경우를 핸들링 하기 위해 존재하는 부분 입니다. 만약 이 경우가 발생한다면, $N^2_{CC}[u_c, v_c, u]$의 값을 1 증가 시킵니다.

Handle $D_1$, $D_2$ Changed DCS Nodes

이 과정에서 $D_1$이나 $D_2$ 값이 업데이트 된다면, 이것의 영향을 받아 자식/부모 노드의 $D_1$, $D_2$ 값도 $0 \rightarrow 1$이 될 가능성이 존재합니다. 그래서 업데이트 스트림을 처리하는 과정에서 $D_1$, $D_2$ 값 변화가 있던 DCS 노드들을 모아서 추가 처리가 필요합니다.

그래서 두는게, $Q_1$, $Q_2$ 이고, 이들은 아래의 DCS 노드들을 저장합니다.

• $Q_1$ stores $<u, v>$ s.t. $D_1[u, v] = 0 \rightarrow 1$
• $Q_2$ stores $<u, v>$ s.t. $D_2[u, v] = 0 \rightarrow 1$

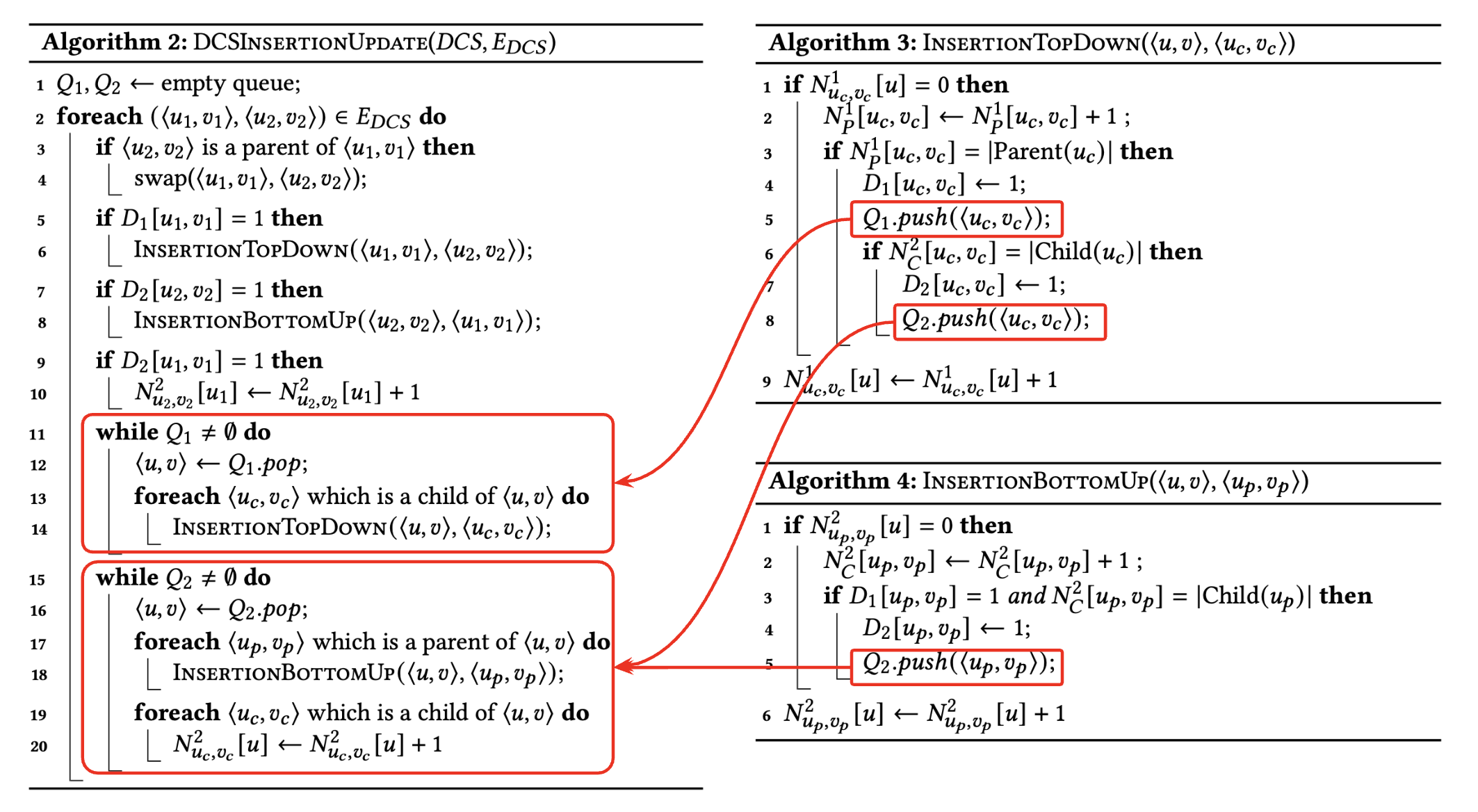
가장 먼저 $Q_1$ 큐의 원소를 비워가면서, 자식 노드에 대해 추가적인 Parent Subgraph Matching이 발생하는지 체크 합니다. [A2-L11 ~ L14] 그리고 이 과정에서 $D_1$ 값 변경이 발생하면, $Q_1$에 추가 삽입이 발생합니다.

그리고 $Q_2$ 큐의 원소를 비워가면서, 부모 노드에 대해 추가적인 Child Subgraph Matching이 발생하는지 체크 합니다. [A2-L15 ~ L20] 마찬가지로 이때도 $D_2$ 값 변경이 발생하면, $Q_2$에 추가 삽입이 발생합니다.

Edge Deletion

지금까지 엣지 삽입을 기준으로 설명을 하였습니다. 그런데, CSM 문제는 Negative Matching을 찾는 것도 수행합니다. 이것은 삽입 때 했던 것을 반대로 수행 하면 됩니다.

1. 엣지 삭제로 영향 받는 Updated parent/child를 모두 찾는다.
2. $D_1$ 또는 $D_2$ 값이 1에서 0으로 바뀌는 경우를 찾습니다.

맺음말

포스트를 적으면서, 이해를 쉽게 하기 위해서 SymBi 논문에서 자료구조를 제시하는 순서나 표기를 바꾼 것들이 좀 있습니다! 그리고 제가 나름대로 이해한 내용을 적은 것이기 때문에 부정확한 내용이나 설명이 있을 수도 있으니 양해 부탁드립니다!

이어지는 포스트에서는 이렇게 업데이트한 DCS 자료구조를 바탕으로 Subgraph Matching을 찾는 “Backtracking” 방법에 대해 살펴보겠습니다.

➡️ Symbi, Find Matching