Paper Reading: SymBi, Find Matching

2025년 저는 데이터베이스 랩에 컨택하여 학부 졸업 연구 주제를 받아서 진행하고 있습니다. 저의 주제는 “Continuous Subgraph Matching”과 관련해 코드를 최적화 하고 개선하는 것으로 그래프 쿼리 관련 논문을 읽고, C++ 코드를 튜닝하고 있습니다. 졸업 마지막 학기에 듣는 수업인데 많은 노하우와 경험을 쌓고 졸업하기를 기대하고 있습니다 ㅎㅎ

Matching Algorithm

DCS 구조 위에서 모든 positive/negative 매칭을 찾는 방법에 대해서 살펴봅니다.

아이디어는 “Partial Embedding”에서 시작해 그게 “Full Embedding”이 될때까지 점점 키워가는 전략 입니다.

Extendable vertex

Partial Embedding을 확장할 때, 아무 노드만 선택할 수는 없습니다. 그래서 Embedding 확장에서 선택할 수 있는 노드를 “Extendable vertex”라고 정의 합니다.

Given a partial embedding $M$, a vertex $u$ of query graph $q$ is called “extendable”

1. if $u$ is not mapped to a vertex of $g$ in $M$
2. at least one neighbor of $u$ is mapped to a vertex of $g$ in $M$

정의는 아주 직관적인데, (1) 아직 매핑되지 않은 노드 여야 하고, (2) 이미 매핑된 녀석과 연결 되어 있어야 합니다.

Extendable Candidates $C_M(u)$

Partial Embedding을 확장할 쿼리 노드를 고른 다음에는 그 쿼리 노드를 데이터 그래프의 노드 중 어떤 녀석에 매핑할지도 결정해야 합니다.

일단 매핑 가능한 데이터 노드도 여러 개 있을 텐데, 그걸 “Extendable Candidate”라고 부릅니다.

Given a query vertex $u$, a data vertex $v$ is its “extendable candidate”

if $v$ satisfies the following conditions

• $D_2[u, v] = 1$
  • i.e. it’s not filtered in the DCS structure
• For all matched neighbors $u’$ of $u$, $(M(u’), v) \in E(g)$
  • i.e. preserve the connectivity

이 정의도 아주 직관적이다. 일단 우리가 DCS에서 열심히 구한 $D_2$ 값이 1이어야 한다. 지금까지 모두 이걸 위해서 $N^2_C$, \(N^2_{CC}\)를 정의한 것이다 ㅋㅋ

그리고 지금까지 Partial Embedding에 있던 쿼리 노드가 매핑한 데이터 노드 $M(u’)$와 새로 매핑하려는 데이터 노드 $v$ 사이의 연결성이 데이터 엣지로 존재해야 한다. (당연 ㅋㅋ)

이 Extendable Candidates를 $C_M(u)$라고 표기하고, 수학적으로 아래와 같이 적습니다.

\[C_M(u) = \left\{ v \; : \; v \in C(u) \quad \text{and} \quad D_2[u, v] = 1 \quad \text{and} \quad \forall u' \in \text{Nbr}_M(u), \; (M(u'), v) \in E(g) \right\}\]

표기에서 $\text{Nbr}_M(u)$는 쿼리 노드 $u$와 이웃한 노드 중에서 이미 매핑 $M$에 포함된 것들을 말합니다.

점점 등장하는 기호들이 많아지면서 논문을 읽을 때 헷갈리더라구요 ㅋㅋ 명확히 하기 위해 정리하면

• 당연히 $\text{Nbr}_M(u) \subseteq \text{Nbr}(u)$ 입니다.
• 그리고 당연히 $C_M(u) \subseteq C(u)$ 입니다.

Find Matches

그래서 Partial Embedding을 확장하는 절차를 간단히 기술하면 아래와 같습니다.

1. 주어진 Partial Embedding에서 Extendable 모든 쿼리 노드를 찾습니다.
2. 그중 하나의 쿼리 노드를 선택합니다.
   • 이때, Extendable 여러 쿼리 노드 중에서 어떤 걸 선택할지도 중요 합니다.
   • 랜덤하게 선택할 수도 있고,
   • 가치를 평가한 후 “Matching Order”를 부여하여 선택할 수도 있습니다.
3. Extendable 쿼리 노드를 선택 했다면, 데이터 그래프에서도 “Extendable 후보”들을 찾는다.
4. 모든 Extendable 후보들을 순회하며, 이를 Partial Embedding에 포함하여 확장 시킨다.
5. [1-4] 과정을 반복 한다.

논문에서는 아래와 같이 코드를 제시 합니다.

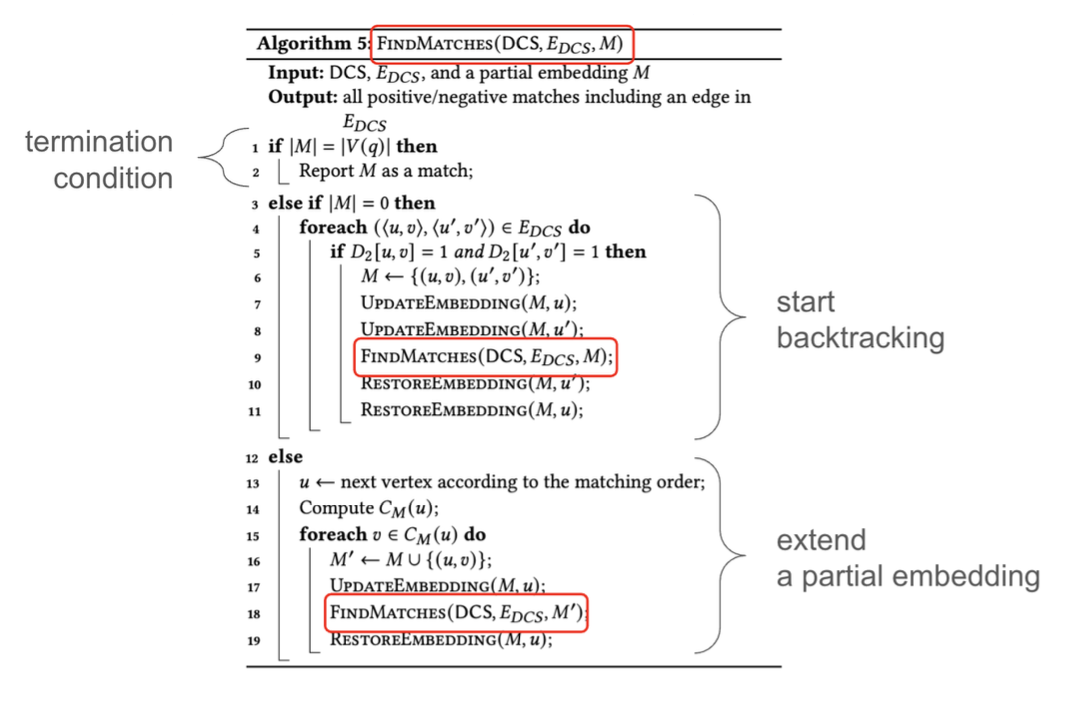
지금은 이 과정이 재귀의 형태로 진행된다는 것만 확인 합니다.

Extendable Partial Candidates

Extendable Candidate $C_M(u)$는 쿼리 노드 $u$가 주어지면, 이것에 대한 매핑 가능한 데이터 노드를 찾은 것 이었습니다.

\[C_M(u) = \left\{ v \; : \; v \in C(u) \quad \text{and} \quad D_2[u, v] = 1 \quad \text{and} \quad \forall u' \in \text{Nbr}_M(u), \; (M(u'), v) \in E(g) \right\}\]

이것을 변형해서 아래와 같은 보조 집합을 정의 합니다.

논문에서는 $S[u, u’]$가 아니라 $S_{u’}$라고 표기하지만, 저는 표기가 너무너무 헷갈려서 이 부분도 저만의 표기로 작성하겠습니다. 그리고 이름도 논문에서는 부여한 적이 없지만 저는 지칭을 좀 하고 싶어서 “Extendable Partial Candidate”라고 이름 붙였습니다. (길다길다…)

쿼리 노드 $u$와 그것의 이웃 $u’ \in \text{Nbr}_M(u)$가 있을 때, 매핑 가능한 데이터 노드의 집합을 아래와 같이 정의한다.

\[S[u, u'] = \left\{ v \; : \; v \in C(u) \quad \text{and} \quad D_2[u, v] = 1 \quad \text{and} \quad (M(u'), v) \in E(g) \right\}\]

이때, $S[u, u’]$의 집합이 $C_M(u)$보다 큰 집합 입니다.

\[\forall u' \in \text{Nbr}_M(u), \quad C_M(u) \subseteq S[u, u']\]

그리고

\[C_M(u) = \bigcap_{u' \in \text{Nbr}_M(u)} S[u, u']\]

예시를 통해 살펴봅시다.

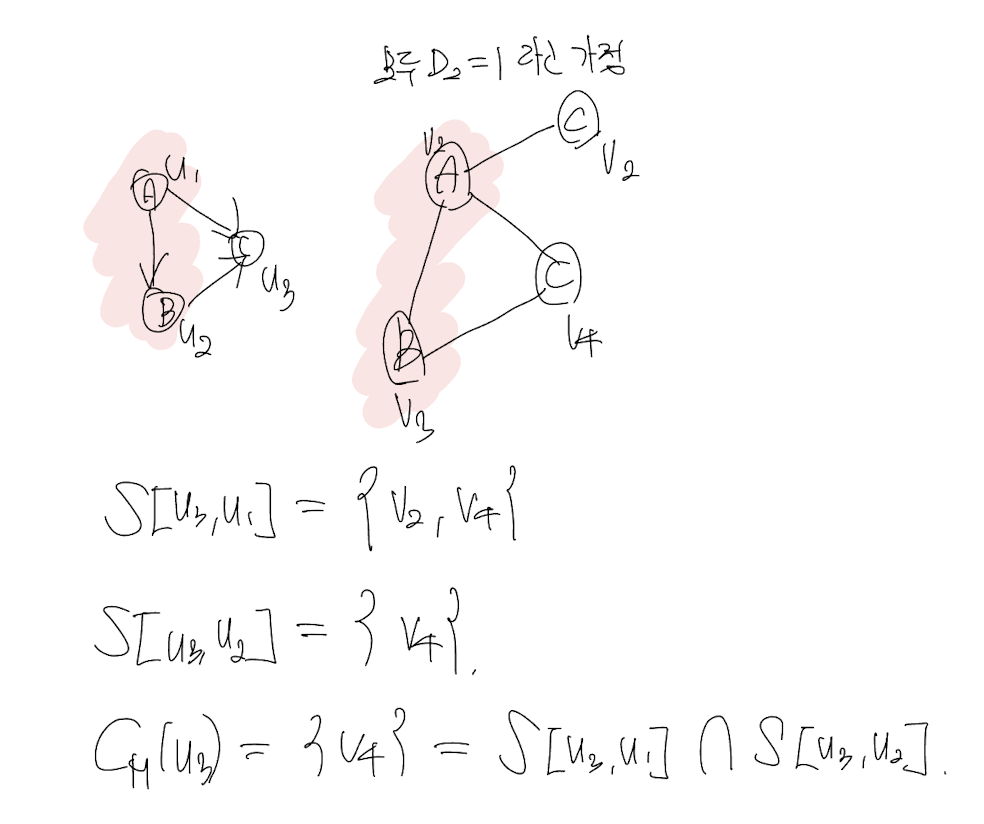
논의의 편의를 위해 모든 데이터 노드는 $D_2 = 1$라고 가정했습니다. (물론 예시로 그린 그림에서는 $v_2$에 대해 $D_2 \ne 1$이지만!)

이 경우, $S[u_3, u_1]$가 더 큰 가능한 집합 제공합니다. 이것은 $S[u_3, u_1]$는 $(u_1, u_3) \in E(q)$ 사이 연결성만 고려해서 Extendable candidates를 찾기 때문입니다.

그래서 $C_M(u)$는 이런 것들의 모든 공통 분모를 모은 것 입니다. 그래야 모든 이웃 $u’ \in \text{Nbr}_M(u)$에 대해서 연결성이 보존되기 때문입니다.

Improved Extendable Candidates Computing

여기에서 가장 작은 크기를 갖는 “Extendable Partial Candidate”를 찾아서 그 이웃 쿼리 노드 $u’$를 $u_{min}$라고 정의 합니다.

\[u_{min} = \underset{u' \in \text{Nbr}_M(u)}{\text{argmin}} \left\vert S[u, u'] \right\vert\]

오케이! 그런데 $u_{min}$을 왜 정의한 걸까요…?? 그 이유는 $C_M(u)$가 모든 $S[u, u’]$의 “교집합“으로 정의되기 때문입니다! 그래서 가장 작은 집합을 만드는 쿼리 노드를 알고 있다면, 그 녀석이 만들어내는 Partial Candidates를 사용해서 실제로 Extendable Candidates $C_M(u)$를 찾아내는 것이 훨씬 효율적이기 때문입니다!

그래서 $C_M(u)$에 대한 식이 기존식에서 아래와 같이 바뀝니다.

[기존 버전]

\[C_M(u) = \left\{ v \; : \; v \in C(u) \quad \text{and} \quad D_2[u, v] = 1 \quad \text{and} \quad \forall u' \in \text{Nbr}_M(u), \; (M(u'), v) \in E(g) \right\}\]

[개선된 버전]

\[C_M(u) = \left\{ v \; : \; v \in S[u, u_{min}] \quad \text{and} \quad D_2[u, v] = 1 \quad \text{and} \quad \forall u' \in \text{Nbr}_M(u), \; (M(u'), v) \in E(g) \right\}\]

이렇게 하면 기존의 탐색 공간이 \(O(C(u) \times \text{Nbr}_M(u))\)에서 $O(S[u, u_{min}] \times \text{Nbr}_M(u))$으로 줄어듭니다!

참고로 논문에서는 $S[u, u_{min}]$을 $S_{min}[u]$로 표현합니다.

Relation with Child Candidate Array $N^2_{CC}$

DCS 업데이트를 위해 계산 했던 Child Candidate 갯수가 저장된 $N^2_{CC}$의 정의와 값을 다시 생각해봅시다.

$N^2_{CC}[u, v, u_c]$에는 DCS의 노드 $<u, v>$와 연결된 $C(u_c)$ 중에서 $D_2[u_c, v_c] = 1$인 $v_c$ 들의 갯수 입니다.

이것을 DCS의 노드 $<u’, M(u’)>$와 연결된 $C(u)$ 중에서 $D_2[u, v] = 1$인 $v$의 갯수를 저장한 것은 $N^2_{CC}[u’, M(u’), u]$가 됩니다.

그런데, 잠깐!!! “이것은 $S[u’, u]$의 정의와 정확히 일치” 합니다! 따라서 아래의 등식이 성립 합니다.

\[\vert S[u, u'] \vert = N^2_{CC} [u', M(u'), u]\]

그럼 이제 $u_{min}$ 쿼리 노드를 찾는 것도 집합 사이즈를 직접 구할 필요 없이 기존에 계산 했던 $N^2_{CC}$의 값을 기반으로 찾으면 됩니다!

이제 논문에서 코드로 제시된 알고리즘을 살펴봅시다!

지금가지 설명한 내용이 잘 담겨 있죠?? ㅎㅎ

Matching Order

Partial Embedding을 확장하는 과정을 다시 봅시다.

1. 주어진 Partial Embedding에서 Extendable 모든 쿼리 노드를 찾습니다.
2. 그중 하나의 쿼리 노드를 선택합니다.
   1. 이때, Extendable 여러 쿼리 노드 중에서 어떤 걸 선택할지도 중요 합니다.
   2. 랜덤하게 선택할 수도 있고,
   3. 가치를 평가한 후 “Matching Order“를 부여하여 선택할 수도 있습니다.
3. Extendable 쿼리 노드를 선택 했다면, 데이터 그래프에서도 “Extendable 후보”들을 찾는다.
4. 모든 Extendable 후보들을 순회하며, 이를 Partial Embedding에 포함하여 확장 시킨다.
5. [1-4] 과정을 반복 한다.

여기에서 [2번] 단계에서 Extendable 쿼리 노드 중 어떤 쿼리 노드를 선택할지 정해야 합니다. 물론 Embedding을 찾기 위해서는 결국 모든 쿼리 노드를 빠짐없이 선택하게 되겠지만, 확장 과정에서 어떤 쿼리 노드를 먼저 선택하느냐에 따라서 더 빨리 Pruning 하고 탐색을 종료할 수 있기 때문입니다.

만약, Embedding을 확장하다가 마지막에 하나의 쿼리 노드를 남겨두고 Matching이 실패한다면 그때까지 확장에 든 코스트가 무척 아깝게 됩니다.

즉, “Matching이 없다”는 같은 결과를 받게 되더라도, 확장할 쿼리 노드를 선택하는 순서에 따라 빨리 SM을 빠르게 종료할 수 있다는 의미 입니다.

Symbi 논문에서는 확장 순서를 “Size of Extendable Candidates”, 즉, $C_M(u)$의 크기를 기준으로 작은 것부터 선택해 확장하는 것을 제안 합니다.

Estimation of Extendable Candidates

그러나 $C_M(u)$ 집합을 계산하는 것은 high-cost 작업 입니다. Extendable Vertex는 매 과정마다 동적으로 변하고, 이것들의 $C_M(u)$ 집합도 매번 변할텐데 이걸 모두 다시 계산하고, 그 중에서 하나만 선택해 사용하기에는 비효율적이다는 것을 SymBi에서 주장 합니다.

그래서 아까 앞에서 $C_M(u)$의 계산 사이즈를 줄이기 위해 사용한 $S_{min}[u]$의 성질을 사용해 이 사이즈를 추정 합니다!

개선된 $C_M(u)$의 정의에 따라 $\left\vert C_M(u) \right\vert$의 크기는 $\left\vert S_{min}[u] \right\vert$의 크기보다 클 수 없습니다.

\[\left\vert C_M(u) \right\vert \le \left\vert S_{min}[u] \right\vert\]

따라서, $\left\vert S_{min}[u] \right\vert$ 값을 추정치로 사용해 가장 작은 값을 가진 Extendable 쿼리 노드 $u$를 골라서 Embedding 확장을 진행 합니다.

Symbi에서는 이것을 $Est(u)$로 정의합니다.

논문에서는 $E(u)$로 정의했지만, edge set $E(q), E(g)$ 표기와 헷갈릴 것 같아서 $Est(u)$로 표기를 바꿉니다.

\[Est(u) = \underset{u' \in \text{Nbr}_M(u)}{\text{argmin}} \left\{ N^2_{CC}[u', M(u'), u] \right\} = \underset{u' \in \text{Nbr}_M(u)}{\text{argmin}} \left\{ \left\vert S[u, u']\right\vert \right\}\]

Isolated Vertices

아직도 뭐가 남았다? SymBi에서는 CFL-Match(2016) 논문에서 사용한 Leaf Decomposition 테크닉에서 아이디어를 얻어서 이를 적용합니다.

CFL-Match는 쿼리 그래프를 Forest-Leaf 구조로 분할 하였습니다. Leaf 노드는 이웃이 딱 하나만 있는 노드를 말합니다. CFL-Match의 아이디어는 “Leaf 노드들에 대한 매칭을 가능한 나중으로 미루는 것” 입니다.

CFL에서는 non-leaf vertex를 먼저 매칭할 때, 아래와 같은 이점이 있다고 주장 합니다.

• 아직 매칭되지 않은 이웃들이 새로운 Extendable Candidate가 됨.
  • 즉, 확장을 통해 Extendable Candidate의 사이즈가 커질 수 있습니다.
  • 반면에, Leaf 노드를 먼저 매칭하면, Extendable Candidate의 사이즈는 항상 줄어들거나 유지 됩니다.
• 그리고 non-leaf의 경우, Extendable Candidate $C_M(u)$의 사이즈도 left 노드의 경우보다 더 적습니다. 왜냐하면, 이웃과 더 많이 연결된 쿼리 노드일수록 더 적은 $C_M(u)$를 가질 것으로 예상 되기 때문입니다. (교집합에 의해서!)

따라서 이 기법은 탐색 공간을 줄여서 매칭 속도를 높이는게 기여 합니다.

SymBi에서는 이 Left 노드의 개념을 확장하여 아래와 같이 정의합니다.

For a query graph $q$ and a data graph $g$, and a partial embedding $M$,

an “isolated vertex” is an extendable vertex in $q$ where all of its neighbors are mapped in $M$.

기존의 left 노드는 하나의 이웃이 있는 경우를 말했지만, “Isolated Vertex”는 모든 이웃 노드가 Partial Embedding으로 매핑된 경우를 말합니다.

예시 쿼리 그래프를 그려보면 아래와 같습니다. 그림에서 파란색으로 색칠만 노드들이 Isolated Vertex들 입니다.

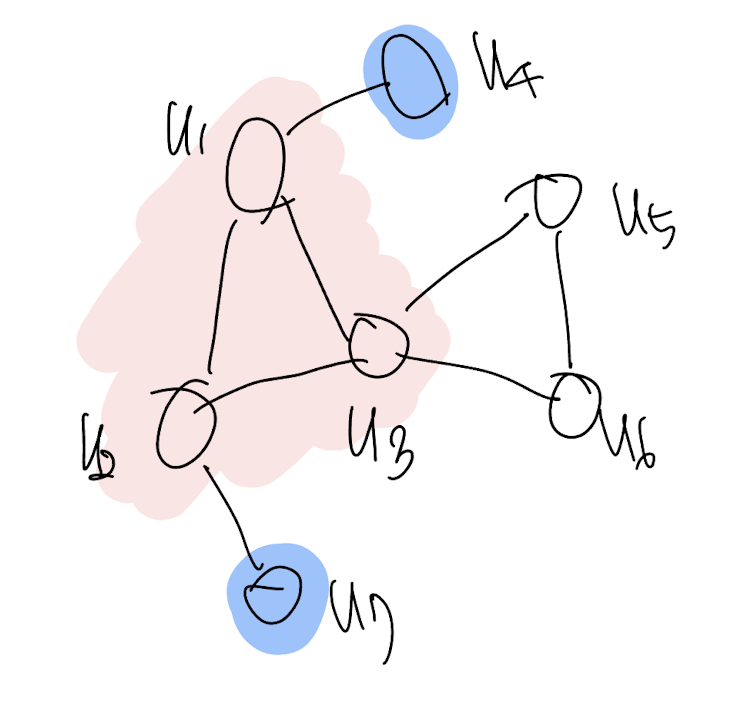
CLF처럼 SymBi 논문에서도 “Isolated Vertex”로 매칭을 확장하는 것을 최대한 미룹니다!

• Isolated Vertex를 매칭하는 것은 Extendable Vertex 공간을 늘리지 않습니다.
  • Isolated Vertex로 연결된 이웃 정점이 없거나 이미 모두 매칭된 상태이기 떄문입니다.
• 모든 Leaf 노드는 Isolated 노드가 됩니다.
  • 그래서 Isolated 노드의 평가를 미루는 것은, Leaf 노드의 평가를 미루는 것이 포함 합니다.

Matching Order 방식과 Isolated Vertex의 평가를 미루는 것을 조합한 최종 형태는 아래와 같습니다.

1. 만약 Isolated Vertex가 존재하는데,
   • 그것의 매칭 가능한 $C_M(u) = \emptyset$인 상황이라면,
     • 이것은 절대 Full Embedding에 도달할 수 없다. 과정을 종료 한다.
   • 만약 $C_M(u) \ne \emptyset$라면,
     • 괜찮다! Isolated Vertex $u$는 무시하고, non-isolated vertex가 있는지 찾는다.
2. 만약 non-isolated vertex가 있다면
   • 그중에서 가장 작은 $Est(u)$ 값의 노드를 선택해 확장한다.
3. 만약 모든 extendable 노드가 isolated vertex라면
   • (어쩔 수 없다) 그중에서 가장 작은 $Est(u)$ 값의 노드를 선택해 확장한다.

맺음말

휴우… 드디어 SymBi 논문의 아이디어를 모두 살펴보았다. 연구실에서 논문 리딩을 하고 발표를 위해 이해하고 정리 했던 내용을 블로그로 옮겨왔는데, 다시 옮기면서 나도 이 알고리즘에 대한 이해가 깊어진 것 같다 ㅎㅎ

혹시 언젠가 다른 누군가가 어떤 연구실에서 SymBi 논문을 읽게 된다면 이 자료가 도움이 되기를 ㅎㅎ ✌️